 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Інтегрування раціональних функцій
Нагадаємо, що раціональною функцією називається функція вигляду:
Інтеграли від раціональних функцій завжди виражаються через елементарні функції. У деяких випадках до таких інтегралів можна звести інтеграли від інших класів функцій (ірраціональних, тригонометричних). Тому вміння інтегрувати раціональні функції вельми необхідно. Виконання цієї задачі ґрунтується на наступному: Розглянемо спочатку випадок 1. Знаменник ся до одного з наступних чотирьох типів:
I. II. III. IV. 2. Кожному множнику ставиться у відповідність елементарний дріб, або сума елементарних дробів. А саме: Множнику I типу ставиться у відповідність дріб Множнику II типу ставиться у відповідність сума дробів:
Множнику III типу ставиться у відповідність дріб Множнику IV типу ставиться у відповідність сума дробів:
Коефіцієнти в чисельниках цих дробів поки що невизначені числа. 3. Підінтегральний дріб тарних дробів. Потім ця сума приводиться до спільного знаменника, який очевидно співпадає з Нагадаємо, що тут ми припускали, що Перейдемо до розглядання прикладів. Приклади. 1. Степінь чисельника співпадає зі степінню знаменника. Виділимо в підінтегральному дробу цілу частину:
Тоді:
Розкладемо на множники знаменник підінтегрального дробу:
Звідси бачимо, що всі множники відносяться до I типу. Тому підінтегральний дріб запишеться так:
Зводячи тепер суму у правій частині до спільного знаменника, отримуємо:
Зрівняємо коефіцієнти при однакових степенях
Розв’язуючи цю систему, одержимо: Зауважимо, що ці значенні можна було отримати інакше. Оскільки отриманий чисельник співпадає з чисельником
Іноді є сенс комбінувати обидва методи знаходження коефіцієнтів. Таким чином маємо:
Отже
2. Степінь чисельника нижча за степінь знаменника, і у знаменнику два множники II типу. Тому:
Зрівнюючи коефіцієнти, отримуємо:
Покладаючи
Покладаючи
Звідси
Звідси
3.
Степінь чисельника вища за степінь знаменника. Виділимо в підінтегральному дробу цілу частину:
Тому
Один множник I типу і один множник III типу. Отже
Зрівнюючи коефіцієнти, маємо:
Звідси:
4.
Степінь чисельника нижча за степінь знаменника, у знаменнику множник
Чисельник, що отримується після приведення до спільного знаменника, має вид:
Покладаючи тут Розкриваючи дужки і зрівнюючи коефіцієнти при однакових степенях
Оскільки вже відомо, що З 1–го рівняння: З 2–го рівняння: З 3–го рівняння: З 4–го рівняння:
Тепер маємо:
Обчислимо окремо:
Підставляючи ці вирази до (8.1), остаточно отримуємо:
Поиск по сайту: |
 , де
, де 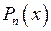 – поліном степеня
– поліном степеня  , а
, а  – поліном степеня
– поліном степеня  .
. , тобто степінь чисельника нижче степеня знаменника.
, тобто степінь чисельника нижче степеня знаменника.
 , де
, де 
 , де
, де 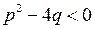
 , де
, де 
 .
. .
. .
. .
. записується у вигляді суми всіх цих елемен-
записується у вигляді суми всіх цих елемен- у отриманому чисельнику і чисельнику
у отриманому чисельнику і чисельнику 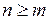 , тобто степінь чисельника вище, або дорівнює степені знаменника, то треба виділити з дроба
, тобто степінь чисельника вище, або дорівнює степені знаменника, то треба виділити з дроба  .
. .
.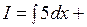
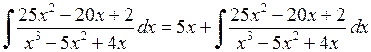 .
. .
. .
.
 .
. , для чого складемо наступну табличку:
, для чого складемо наступну табличку:
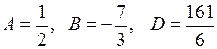 .
. , не розкриваючи дужок, покладемо послідовно
, не розкриваючи дужок, покладемо послідовно  . Отримаємо ті ж самі значення для коефіцієнтів
. Отримаємо ті ж самі значення для коефіцієнтів  .
.
 .
. .
. .
.




 і зрівнюючи чисельники, матимемо:
і зрівнюючи чисельники, матимемо:  .
. , отримуємо:
, отримуємо:  .
. , і система спрощується:
, і система спрощується: .
. . Таким чином маємо:
. Таким чином маємо:
 .
. .
. .
. .
. .
.
 . І тоді
. І тоді

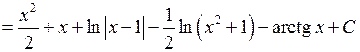 .
. .
. I типу, а множник
I типу, а множник  – IV типу. Маємо:
– IV типу. Маємо: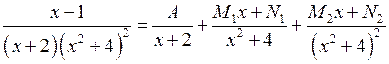 .
. .
. , одержимо
, одержимо  , звідки
, звідки  .
. :
:
 .
.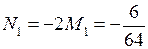 .
. .
. .
.
 . (8.1)
. (8.1) ;
;
 (скористалися формулою (7.2)).
(скористалися формулою (7.2)). .
.