 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод інтегрування за частинами
Нехай
Зінтегруємо обидві частини цієї рівності:
Або:
Формула (5.1) називається формулою інтегрування за частинами. Вона „перекидає” символ диференціала з функції Розглянемо приклади. 1). Оберемо Згідно з формулою (5.1) маємо:
2) Оберемо
Чому ж першого разу ми обрали
Якщо під знаком інтеграла міститься добуток степеневої функції на тригонометричну або показникові функцію (зокрема експоненту), то у якості Якщо під знаком інтеграла міститься добуток степеневої функції на логарифмічну або обернену тригонометричну, то у якості Іноді формулу (5.1) доводиться застосовувати декілька разів. Приклади.
1).
2).
Позначимо даний інтеграл через
Далі:
Найпростіші інтеграли, що містять квадратний тричлен. Серед табличних інтегралів є такі:
Покажемо, що до одного з них можна звести інтеграли вигляду:
Дійсно, виділимо у знаменнику підінтегрального дробу повний квадрат:
Далі можлива одна з 3-х ситуацій. 1)
2)
3)
Зауважимо, що аналогічним чином можна обчислити інтеграли вигляду:
Перейдемо до прикладів.
1.
2.
3.
Розглянемо інтеграл більш загального вигляду:
Виділимо у чисельнику підінтегрального дробу похідну його знаменника:
Тоді наш інтеграл приймає вид:
Перший з цих інтегралів дорівнює Аналогічно обчислюються інтеграли вигляду:
Їх теж можна розбити на два інтеграли, перший з яких має вид:
Розглянемо приклади.
1.
2.
Поиск по сайту: |
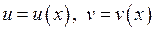 – неперервно диференційовні на деякому проміжку функції. Розглянемо диференціал їх добутку:
– неперервно диференційовні на деякому проміжку функції. Розглянемо диференціал їх добутку: .
. .
.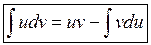 (5.1)
(5.1)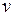 на функцію
на функцію  . Функцію
. Функцію  .
.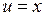 , тоді
, тоді 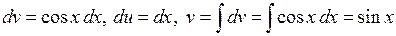 .
. .
.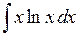 .
.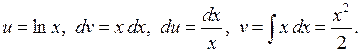 Тоді маємо:
Тоді маємо: .
.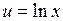 . Ось саме з метою спрощення інтеграла за рахунок формули (5.1). Саме з цих міркувань випливають наступні рекомендації щодо застосування цієї формули.
. Ось саме з метою спрощення інтеграла за рахунок формули (5.1). Саме з цих міркувань випливають наступні рекомендації щодо застосування цієї формули.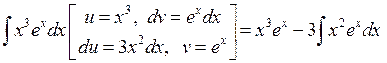
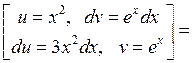

 .
. .
. і застосуємо формулу (5.1), обравши
і застосуємо формулу (5.1), обравши 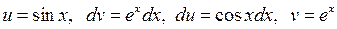 . Тоді
. Тоді .
.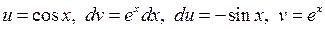 . Отримаємо:
. Отримаємо: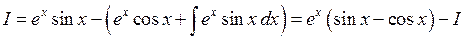 , тобто отримали рівняння відносно
, тобто отримали рівняння відносно  .
.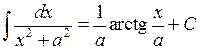 ,
,  .
.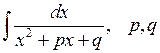 – сталі.
– сталі.
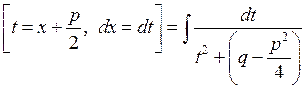 .
.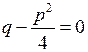 . Тоді інтеграл набуває вигляду:
. Тоді інтеграл набуває вигляду: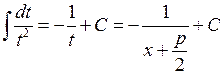 .
. . Тоді, позначивши
. Тоді, позначивши 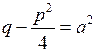 , матимемо:
, матимемо: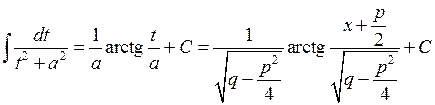 .
. . Тоді, позначивши
. Тоді, позначивши 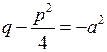 , матимемо:
, матимемо: .
. , (6.1) зводячи їх до одного з інтегралів:
, (6.1) зводячи їх до одного з інтегралів: (при
(при  ).
).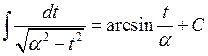 (при
(при 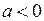 ).
).
 .
.

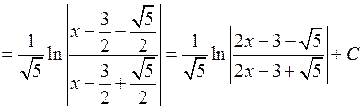 .
.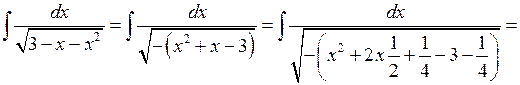

 .
. .
. .
. .
.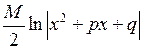 (згідно з формулою (4.2)), а другий обчислюється наведеним вище способом.
(згідно з формулою (4.2)), а другий обчислюється наведеним вище способом. .
. , а другий відноситься до виду (6.1).
, а другий відноситься до виду (6.1).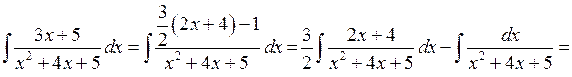
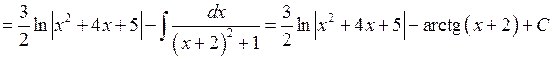 .
.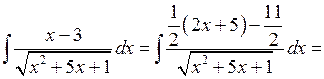


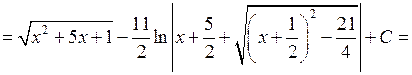
 .
.