 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ІНТЕГРУВАННЯ РАЦІОНАЛЬНИХ ФУНКЦІЙ
Раціональні функції складають важливий клас функцій, інтеграли від яких завжди виражаються через елементарні функції.
Деякі відомості про раціональні функції
Ціла раціональна функція
Означення. Многочленом (поліномом або цілою раціональною функцією) називається функція
де
Означення. Коренем многочлена (4.1) називається таке числове значення Теорема 4.1. (Безу). Остача від ділення многочлена Пояснимо зміст теореми Безу. При діленні многочлена
Теорема стверджує, що
Зокрема, якщо
Таким чином, з теореми Безу випливає Наслідок. Якщо
Виникає запитання. Чи всякий многочлен має корені? Позитивну відповідь на це запитання дає основна теорема алгебри. Теорема 4.2 (основна теорема алгебри).Всякий многочлен степеня З основної теореми алгебри випливає, що многочлен (4.1) завжди можна записати у вигляді (4.4). Неважко помітити (наприклад, з процедури ділення многочлена Приклад 4.1. Поділити многочлен Розв’язання.
Якщо степінь многочлена Теорема 4.3.Всякий многочлен
де
Вираз (4.5) називається розкладом многочлена на лінійні множники Якщо деякі з лінійних множників у виразі (4.5) однакові, то їх можна об’єднати. Тоді розклад (4.5) матиме вигляд
де
Корінь кратності одиниця називається простим. Будемо надалі розглядати тільки многочлени з дійсними коефіцієнтами. Серед коренів представлення (4.6) можуть бути і комплексні числа. Справедливе наступне твердження. Теорема 4.4. Нехай Перемножимо лінійні множники, що відповідають комплексно-спряженим кореням
де Одержано квадратний тричлен
Об’єднуючи у формулі (4.6) множники із комплексно-спряженими коренями, дістанемо
де
Висновок. Всякий многочлен з дійсними коефіцієнтами можна розкласти (і притому єдиним способом) на лінійні та квадратичні (з від’ємним дискримінантом) множники з дійсними коефіцієнтами. Приклад 4.2.Розкласти на множники з дійсними коефіцієнтами многочлени
1)
Розв’язання. 1) Розглянемо квадратний тричлен
де
Знайдемо корені рівняння
Тому
2) Розглянемо многочлен Для розкладання на множники застосуємо спосіб групування:
Перевіримо, чи можна розкласти на лінійні множники з дійсними коефіцієнтами квадратний тричлен
Таким чином, Тому,
3) Легко перевірити підстановкою у многочлен
Маємо:
Оскільки дискримінант квадратного тричлену Кінцевий результат:
Справедливі наступні твердження. Твердження 4.1. Якщо многочлен
Твердження 4.2. Якщо многочлени тотожно дорівнюють один одному, то вони мають рівні степені і рівні між собою коефіцієнти при однакових степенях
Поиск по сайту: |
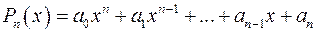 , (4.1)
, (4.1) – степінь многочлена (натуральне число);
– степінь многочлена (натуральне число); – коефіцієнти многочлена (дійсні або комплексні числа).
– коефіцієнти многочлена (дійсні або комплексні числа). (дійсне або комплексне), при якому многочлен перетворюється в нуль, тобто
(дійсне або комплексне), при якому многочлен перетворюється в нуль, тобто 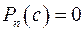 .
. на різницю
на різницю  дорівнює
дорівнює  .
.
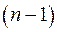 -го степеня і остачу
-го степеня і остачу  – певне число:
– певне число: . (4.2)
. (4.2) .
. . (4.3)
. (4.3)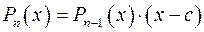 . (4.4)
. (4.4) має хоча б один корінь (дійсний або комплексний).
має хоча б один корінь (дійсний або комплексний). «у стовпчик»), що старший коефіцієнт многочлена
«у стовпчик»), що старший коефіцієнт многочлена  , дорівнює
, дорівнює  .
. на двочлен
на двочлен  «у стовпчик».
«у стовпчик».

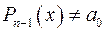 , то до цього многочлена знов можна застосувати теорему 4.2 і наслідок з теореми Безу. Продовжуючи цей процес, приходимо до такого твердження.
, то до цього многочлена знов можна застосувати теорему 4.2 і наслідок з теореми Безу. Продовжуючи цей процес, приходимо до такого твердження. , (4.5)
, (4.5) – корені многочлена;
– корені многочлена;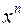 ).
).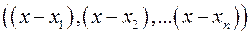 .
. , (4.6)
, (4.6) – число різних коренів;
– число різних коренів;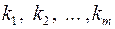 – цілі числа, що називаються крайностями коренів
– цілі числа, що називаються крайностями коренів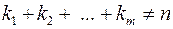 .
.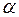 + і
+ і  – комплексний корінь многочлена (4.1) з дійсними коефіцієнтами. Тоді комплексно-спряжене число
– комплексний корінь многочлена (4.1) з дійсними коефіцієнтами. Тоді комплексно-спряжене число 
 ,
, ,
, 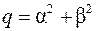 – дійсні числа.
– дійсні числа. з дійсними коефіцієнтами і від’ємним дискримінантом
з дійсними коефіцієнтами і від’ємним дискримінантом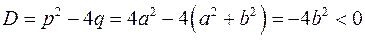 .
.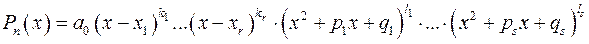 .
. – кратності дійсних коренів;
– кратності дійсних коренів;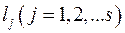 – кратності комплексно-спряжених коренів;
– кратності комплексно-спряжених коренів; ;
; ;
;  – дійсні числа
– дійсні числа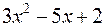 ; 2)
; 2) 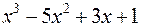 ; 3)
; 3)  .
. . При розкладанні на множники квадратного тричлена
. При розкладанні на множники квадратного тричлена  у випадку
у випадку  користуються формулою
користуються формулою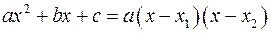 ,
, – корені рівняння
– корені рівняння  , що знаходяться за формулою
, що знаходяться за формулою .
.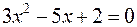 .
. ,
,  .
. .
.

 .
. . Обчислимо його дискримінант
. Обчислимо його дискримінант  . Дискримінант додатній. Обчислимо дійсні корені квадратного тричлена
. Дискримінант додатній. Обчислимо дійсні корені квадратного тричлена .
. .
. .
. , що
, що  є коренем многочлена. За наслідком з теореми Безу (4.4) даний многочлен ділиться без остачі на двочлен
є коренем многочлена. За наслідком з теореми Безу (4.4) даний многочлен ділиться без остачі на двочлен 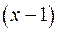 . Виконаємо це ділення «у стовпчик».
. Виконаємо це ділення «у стовпчик».

 .
.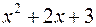
 , то здійснити розклад квадратного тричлену на лінійні множники з дійсними коефіцієнтами неможливо.
, то здійснити розклад квадратного тричлену на лінійні множники з дійсними коефіцієнтами неможливо. ), то всі його коефіцієнти дорівнюють нулю.
), то всі його коефіцієнти дорівнюють нулю.