 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод заміни змінної (підстановки). Суть цього методу полягає у введенні нової змінної інтегрування
Суть цього методу полягає у введенні нової змінної інтегрування, що дає змогу звести інтеграл, який не обчислюється безпосередньо, до табличного або відомого інтеграла. Метод ґрунтується на властивості інваріантності формул інтегрування.
Властивість інваріантності формул інтегрування
Теорема. Будь-яка формула інтегрування зберігає свій вигляд при підстановці замість незалежної змінної х довільної функції
то
Зауваження 1. Твердження (2.1) теореми можна записати у розгорнутому вигляді:
2. В основі доведення цієї теореми лежить властивість інваріантності форми першого диференціала.
Приклад 2.4.
На основі (2.1) справедливо:
Зокрема, підставляючи послідовно
Отже, властивість інваріантності формул інтегрування значно розширює таблицю інтегралів. З відомих формул для диференціалів
випливає справедливість наступних рівностей:
називають введенням функцій Операція введення функції під знак диференціала виконується з ціллю використання властивості інваріантності формул інтегрування у вигляді (2.2). Розглянемо умови їх застосування і наведемо приклади.
Операція введення функції під знак диференціала
Нехай треба знайти складний для безпосереднього інтегрування
в якому підинтегральний вираз
де для функції
введення функції під знак диференціала властивість інваріантності формул інтегрування (2.2)
Приклад 2.5. Знайти інтеграли:
1)
4)
Розв’язання. 1)
2)
3)
4)
5)
6) Звертаємо увагу, що інтеграл
Зауваження.
1. На практиці часто користуються формулами, які є узагальненнями результатів прикладів 1) і 2), а саме:
2. Доцільно пам’ятати наступні формули для диференціалів, що найбільш часто зустрічаються на практиці:
Таким чином, у випадках, коли треба знайти
Можна користуватися записом (2.1) цієї властивості
в якому
Поиск по сайту: |
 , що має неперервну похідну, тобто якщо
, що має неперервну похідну, тобто якщо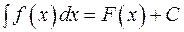 ,
, . (2.1)
. (2.1) . (2.2)
. (2.2) (табличний інтеграл 2,
(табличний інтеграл 2,  ).
). , де
, де  .
. ,
,  ,
,  , маємо
, маємо ;
; ;
; і т.д.
і т.д.
 ; (2.3)
; (2.3) ; (2.4)
; (2.4) . (2.5)
. (2.5)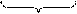


 Перехід
Перехід 



 під знак диференціала. В рівностях виразів (2.4) і (2.5) під знак диференціала введено
під знак диференціала. В рівностях виразів (2.4) і (2.5) під знак диференціала введено  і
і  , відповідно.
, відповідно. , (2.6)
, (2.6) можливо представити у вигляді:
можливо представити у вигляді: , (2.7)
, (2.7) відома первісна
відома первісна  , а
, а 
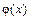
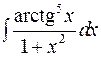 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  .
.
 .
.
 .
.
 .
.
 .
.
 .
.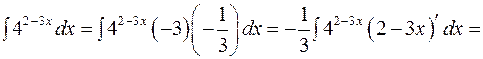
 .
. ;
; .
. ;
;  ;
; ;
;  ;
; ;
;  ;
; ;
;  ;
;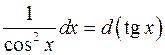 ;
;  .
. .
. , тобто здійснення заміни змінної так званого першого типу.
, тобто здійснення заміни змінної так званого першого типу.