И угловыми характеристиками

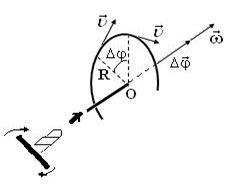
Движение точки по дуге окружности радиуса R называется вра-

щательным движением рис (4.1). Линия перпендикулярная плоскости

вращения (плоскости в которой лежит траектория) и проходящая через

центр окружности (точка О) называется осью вращения. Изменение по-

ложения точки при вращательном движении характеризуют углом пово-

рота Dj радиуса кривизны траектории (измеряют в радианах).

Направление

поступатель-

ного движения

Рис.4.1

Угол поворота удобно представить в виде вектора Dj : вектор

Dj численно равен углу поворота Dj и направлен вдоль оси вращения

согласно правилу правого винта. При вращении правого винта (буравчи-

ка) по направлению вращения, направление поступательного движения

буравчика “показывает” направление вектора Dj

Угловая скорость вращения равна первой производной от угла

поворота :

r dj dj

dt dt

Вектор w направлен так же, как и вектор dj (т.е. Dj при Dt®0)

(уравнение (4.1), рис. 4.1). Вращение с постоянной угловой скоростью

называется равномерным. В этом случае:

ω = , (4.2)

где j - угол поворота за время t.

Равномерное вращательное движение характеризуют периодом

вращения Т - это время одного оборота (т.е. время поворота радиуса вра-

щения на угол 2p). Из (4.2) получим для равномерного вращательного

движения (взяв t = T и, соответственно, j = 2p )

ω = (4.3)

Число оборотов в единицу времени n равно:

. (4.4)

(Понятие периода Т и числа оборотов n можно использовать и для нерав-

номерного вращательного движения, принимая за эти величины те значе-

ния, которые имела бы точка, если бы она вращалась равномерно с дан-

ным значением мгновенной скорости). Из (4.1) , (4.2) и определений Т и n

следует:

[w]=рад/с=1/с=с^-1

[T]=c; [n]=обороты/с=1/с=с^-1

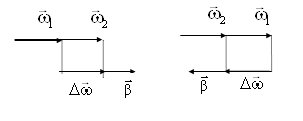
Вектор w может меняться как вследствие изменения скорости

вращения вокруг оси (т.е. изменяется величина w), так и вследствие пово-

рота оси вращения (т.е. меняется направление вектора w ). Пусть за время

Dt вектор w изменился на Dw . Угловое ускорение b равно:

r r r

(4.5)

dt²

Угловое ускорение есть первая производная от угловой скорости или

вторая производная от угла поворота по времени Если ось вращения не

меняет своего направления, то изменения w зависит только от изменения

его величины Следовательно, для неизменного направления оси вращения

из (4.5) получим:

dω d j

dt dt²

В этом случае, при увеличении величины w вектор Dw совпадает с век-

тором w (рис 4.2), при уменьшении – противоположен (рис. 4.3).

Рис.4.2 Рис.4.3

r

Из сказанного и уравнения (4.5) следует: направление вектора b совпа-

дает с направлением вектора w при ускоренном вращении, и противопо-

ложно направлению w при замедленном.

ds

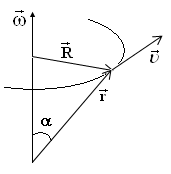
Найдем связь линейных характеристик

движения (u, a, a_n , a_t ) с угловыми

(w, b). Из рис.4.4 видно:

dS dj

d S = dj×R ^⇒ _dt ⁼ _dt ^{R ⇒}

u=wR . (4.7)

(Учитывая правило векторного произведения можно записать (рис.4.4а):

r r r

тор u перпендикулярен w и r т.е. пер-

пендикулярен R ).

Т.к. a_n = ⇒ то, учитывая (4.7), полу-

чим: a_n = = ⇒

Рис.4.4а

a_n= w R . (4.8)

Если ось вращения не меняет своего положения в пространстве, то (с уче-

том (4.7)):

Если при этом R = const , то получим : b = × ⇒ b = ⇒

a_τ = β × R

Из (3.8) , (4.8) и (4.9) находим:

a = (ω² × R)² + (β × R)² = R ω⁴ + β²

Пример: равноускоренное вращательное движение по окружности радиу-

са R: b=const⇒ a_t=bR=const

Из (4.6): dω = β × dt ⇒ dω = β × dt ⇒

ω₀ 0

w-w₀=bt w=w₀+ bt; (см. 3.10). (4.10)

j

dj = ω × dt ⇒ = + β × t)dt ⇒

j₀ 0

j -j₀ = ω₀t +

(см. 3.11 и 3.12).

∆j = ω₀t +

Т.к.

S = ∆j × R ⇒ = ω₀t + ⇒ S = ω₀Rt + ,

wR=u₀, bR= a_t ⇒

a_τ ×t²

S = u₀t + (см. 3.11 и 3.12). (4.12)

Глава 2. Динамика

Поиск по сайту: