 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
НЕПОСРЕДСТВЕННОЕ ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВСтр 1 из 2Следующая ⇒
ГЛАВА1 КРАТНЫЕ ИНТЕГРАЛЫ ДВОЙНЫЕ ИНТЕГРАЛЫ ЛАБОРАТОРНАЯ РАБОТА 1 НЕПОСРЕДСТВЕННОЕ ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ
 ОБЛАСТИ Di через di= ОБЛАСТИ Di через di=  и назовём и назовём
Эта сумма называется ИНТЕГРАЛЬНОЙ СУММОЙ функции f(x,y) при разбиении области D на частичные области Di и выборе точек Mi из частичных областей Di def1: Число I называется ПРЕДЕЛОМ ИНТЕГРАЛЬНОЙ СУММЫ при d®0 области D на частичные области Di на частичные области Di def2: Если существует конечный предел
Если область D задана неравенствами a£x£b y1(x)£y£y2(x), где y1(x), y2(x) интегрируемые функции на [a,b], то соответствующий двойной интеграл может быть вычислен по формуле:
следующие свойства двойных интегралов 1) 2) 3) Если область интегрирования D разбита на две области D1 и D2, то
Пример1 Вычислить Решение: Пример2: Вычислить y= 2-x2 , y= 2x-1 Решение: построим область D. Первая линия- парабола, симметричная относительно оси Oy с вершиной в точке (0,2) Вторая линия- прямая.
 
пересечения A и B: A(-3;-7), B(1,1)
Пример3: Поменять порядок интегрирования
Решение: область интегрирования ограничена линиями: x=-1, x=1, y= 1-x2, Задания 1) Вычислить 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 2) Вычислить 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 3) Поменять порядок интегрирования 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 4) Расставить пределы интегрирования в том и в другом порядке в двойном интеграле 1. S трапеция с вершинами О(0;0),А(2;0), В(1;1), С(0;1). 2. S прямоугольник с вершинами О(0;0),А(2;0), В(2;1), С(0;1). 3. S треугольник с вершинами О(0;0),А(1;0), В(1;1).. 4. S параллелограмм с вершинами А(1;2), В(2;4), С(2;7),D(1;5). 5. S круговой сектор ОАВ с центром в точке О(0;0), у которого концы дуги А(1;1), В(-1;1). 6. S круговое кольцо, ограниченное окружностями радиусов r=1 и R=2 c общим центром (0;0). 7. Область S заданна неравенством 8. Область S ограниченна линиями 9. S ограниченна гиперболой 10. область S ограниченна линиями х=0, у=0, Ответы 1) 1. 2. 3. 50,4 3. (е-1)2 4. 5. 6. 7. 8. 9. 10.
1.1.2 ЛАБОРАТОРНАЯ РАБОТА 2 ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ Преобразование двойного интеграла от ПРЯМОУГОЛЬНЫХ КООРДИНАТ х, у к ПОЛЯРНЫМ КООРДИНАТАМ
Если область интегрирования D| ограниченна двумя лучами, выходящими из полюса,
где Если область интегрирования не принадлежит к рассмотренному виду, то её разбивают на части, каждая из которых является областью данного вида. Пример1: Перейдя к полярным координатам, вычислить Решение: полагая
Пример2: В двойном интеграле
    
ЗАДАНИЯ 1) С помощью перехода к полярным координатам вычислить двойные интегралы: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 2) В данных задачах перейти к полярным координатам и расставить пределы интегрирования в том и другом порядке. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
3) В двойном интеграле
ОТВЕТЫ. 1) 1. πr2h 6. 2. 3. 4. 5.
ЛАБОРАТОРНАЯ РАБОТА 3 ДВОЙНЫЕ ИНТЕГРАЛЫ КАК ПЛОЩАДЬ Площадь плоской области D равна
Если область D в полярных координатах определена неравенствами
Прамер1: Найти площадь фигуры, ограниченной линиями x+y=6. Решение: определим точки пересечения данных линий
6-y=4y-y2 y2-5y+6=0
Пример2: вычислить площадь фигуры, ограниченной окружностями ρ=1, Решение: найдём координаты точки А, пересечения окружностей
Пример3: Найти площадь фигуры, ограниченной линией x3+y3=axy (петля). Решение: примем за параметр переменную x Пример4: Найти площадь, ограниченную петлёй декартового листа Решение: Преобразуем данное уравнение к полярным координатам Т. е. Оси симметрии петли является луч
Ответ: 1) Найти площадь плоских фигур, ограниченных заданными ниже кривыми: 1. xy=4, x+y-5=0 2. x=y, x=2y, x+y=a, x+3y=a (a>0) 3. xy=a2, xy=b2, y=m, y=n 4. y=x, y=5x, x=1 5. 6. y2=10x+25, y2=6x+9 7. 8. y=0, x=0, x+y=1 9. 10. x2=ay, x2=by, y=m, y=n, 0<a<b, 0<m<n.
2) Вычислить площади плоских фигур, ограниченных заданными кривыми, с помощью преобразования к полярным координатам: 1. (x2+y2)2= 2a2(x2-y2) 2. (x2+2y2)3= xy4 3. 4. x2+y2=2x, y2+x2=4y, y=0, y=x 5. (x+y)3=xy, (x≥0, y≥0) 6. 7. (x2+y2-ax)2=a2(x2+y2), 8. (x2+y2)2= a2x2+b2y2 9. x4+y4= 2a2xy 10. 3) Найти площадь области ограниченной кривыми: 1. r=a(1+cosφ), r=acosφ, (a>0) 2. r= cosφ=1, r=2 (имеется в виду область, не содержащая полюса) 3. ρ=acosφ, ρ=bcosφ, b>a>0 4. ρ=2(1-cosφ), ρ=2 (вне кардиоиды) 5. ρ=2(1+cosφ), ρ=2cosφ 6. ρ=asin3φ, a>0 7. ρ=a(1-cosφ), ρ=a (вне кардиоиды) 8. ρ=acos2φ, 9. ρ=4sinφ, ρ=2sinφ 10. ρ2=a2 sin2φ
ОТВЕТЫ 1) 1. 2. 3. 4. 2 5. πab 6. 7. 8. 9. 10. 2) 1. 2a2 2 3. 27π 4. 3 5. 6. 6 7. 8. 9. 10. 3) 1. 2. 3. 4. 8-π 5. 5π 6. 7. 8. 9. 3π 10. a2
1.1.4. ЛАБОРАТОРНАЯ РАБОТА 4 НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ В МЕХАНИКЕ Если пластинка занимает область D плоскости xOy и имеет переменную поверхностную плоскость
Пусть на плоскости xOy задана система материальных точек А1(х1; у1), А2(х2; у2),…., Аn(хn; уn) с массами m1, m2,…, mn. def1: СТАТИЧЕСКИМ МОМЕНТОМ Мm ЭТОЙ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСИ Ох называется сумма произведений масс этих точек на их ординаты:
Аналогично определяется СТАТИЧЕСКИЙ МОМЕНТ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСИ Оу:
СТАТИЧЕСКИЕ МОМЕНТЫ Мх, Му ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ Ох, Оу вместо сумм (1) и (1|) выражаются соответствующими двойными интегралами:
В случае однородной пластинки γ=const, которую принимают равной γ=1. def2: МОМЕНТОМ ИНЕРЦИИ Ix, Iy СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ Ох, Оу называется сумма произведения масс точек на квадраты их расстояний от соответствующей оси:
МОМЕНТ ИНЕРЦИИ Ix, Iy СИСТЕМЫ ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ Ох, Оу вместо (2) и (2|) выражается соответствующими двойными интегралами:
МОМЕНТ ИНЕРЦИИ пластинки относительно НАЧАЛА КООРДИНАТ равен:
ЦЕНТРОБЕЖНЫЙ МОМЕНТ ИНЕРЦИИ:
КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ пластины можно вычислить по формулам:
В случае однородной пластинки формулы имеют вид:
Пример1 Найти координаты центра тяжести фигуры, ограниченной линиями y2=4x+4y, y2=-2x+4. Решение: поскольку фигура симметрична относительно оси Ох, то
Тогда Пример2: Вычислить момент инерции фигуры, ограниченной кардиоидой ρ=а(1+cosθ), относительно оси Ох. Решение: момент инерции относительно оси Ох равен Перейдём к полярным координатам Пример3: Найти момент инерции круга радиуса R относительно точки, лежащей на окружности. Решение: составим уравнение окружности, проходящей через начало координат, х2+у2=2rx и вычислим момент инерции I0. Получим: ЗАДАНИЕ 1) 1. Найти координаты центра тяжести круглой пластинки х2+у2≤а2, если плотность её вещества в точке М(х,у) пропорциональна расстоянию от точки М| до точки А(а;0) Замечание: применяем полярные координаты 2. найти статический момент однородного тела, имеющего форму прямого конуса (основание радиуса R, высота H) относительно плоскости, проходящей через вершину параллельно основанию. 3. Вычислить статический момент пластинки, имеющей форму прямоугольного треугольника с катетами ОА=а, ОВ=b, относительно катета ОА, если плоскость её в любой точке равна расстоянию точки от катета ОА. 4. Найти массу квадратной пластины со стороной а, если плотность вещества пластины в каждой точке пропорциональна расстоянию этой точки от одной из вершин квадрата и равна μ0 в центре квадрата. 5. Найти координаты центра тяжести однородной пластинки, ограниченной кривыми ay=x2, x+y=2a (a>0)
6. Найти координаты центра тяжести однородной пластинки, ограниченной кривыми 7. Найти координаты центра тяжести однородной пластинки, ограниченной кривыми Замечание: использовать замену х=acos3t, y=asin3t, 0≤t≤ 8. Найти координаты центра тяжести однородной пластинки, ограниченной кривой 9. Найти координаты центра тяжести однородной пластинки, ограниченной кривой Замечание: перейти к полярным координатам. 10. Найти координаты центра тяжести однородной пластинки, ограниченной кривыми ρ=a(1+cosφ), φ=0. 2) 1. Найти центробежный момент инерции Ix,y однородной фигуры, ограниченной кривыми: ax=x2, ax=y2 (a>0). 2. Найти координаты центра тяжести однородной пластинки, ограниченной кривой
3. Найти координаты центра тяжести однородной пластинки, ограниченной кривой 4. Найти координаты центра тяжести однородной пластинки, ограниченной кривыми 5. найти статические моменты относительно координатных осей четверти круга радиуса R. 6. Найти статические моменты круга относительно его касательной. 7. Найти статические моменты полукруга относительно его диаметра. Найти статические моменты относительно координатных осей части плоскости, ограниченной линиями y=x2, y+x=2, y=2. 8. Найти статический момент правильного шестиугольника со стороной а относительно стороны (γ=1). 9. Найти статические моменты относительно координатных осей части плоскости, ограниченной линиями y=x2, y+x=2, y=2. 10. Найти статические моменты однородного тела, имеющего форму прямоугольного параллелепипеда с рёбрами a,b,c относительно его граней. 3) 1. Вычислить момент инерции прямоугольника со сторонами a и b относительно его сторон. 2. Вычислить момент инерции квадрата со стороной а относительно одной из вершин. 3. Вычислить момент инерции треугольника, ограниченного прямыми х+у=2, х=2, у=2 относительно оси Ох. 4. Вычислить момент инерции полукруга относительно его диаметра. 5. Вычислить момент инерции круга относительно его центра. 6. Вычислить момент инерции круга относительно касательной. 7. Вычислить момент инерции фигуры, ограниченной кривой 8. Вычислить момент инерции площади, ограниченной линиями 9. Вычислить момент инерции площади, ограниченной линиями у=4-х2, у=0, относительно оси Ох. 10. Вычислить момент инерции площади эллипса
1.2. Тройные интегралы. 1.2.1. ЛАБОРАТОРНАЯ РАБОТА 1 ТРОЙНОЙ ИНТЕГРАЛ def1: ТРЁХМЕРНЫЙ КООРДИНАТНЫМ ПАРАЛЛЕЛЕПИПЕДОМ называется множество точек (х1, х2, х3)ЄR3 удовлетворяющих условию: аi≤хi≤bi , i=1,2,3 ai, bi ЄR и этот параллелепипед обозначим: П=[a1, b1]*[a2, b3]*[a3, b3] Пусть задана функция f(x)= f(x1, x2, x3) в трёхмерной области ПÌR3. Возьмём разбиение Т данного П плоскостями х=хi параллельными координатным гиперплоскостям. Разобьём на частичные параллелепипеды. В каждом Пj возьмём точку РjÌПj, где Рj=(ej1, ej2, ej3). Обозначим через μ(Пj)- объем частичного параллелепипеда Обозначим через def2: Число I называется ПРЕДЕЛОМ интегральных сумм при диаметре λ→0, если для "ε>0 $δ>0, что для "разбиения Т диаметр которого λ<δ и для " набора точек {Pj} PjЄПj выполняется неравенство:
def3: Функция f(x1, x2,x3) называется ИНТЕГРИРУЕМОЙ в трёхмерном прямоугольном координатном параллелепипеде, если существует конечный предел
и этот предел называется ТРЁХКРАТНЫМ ИНТЕГРАЛОМ функции f(x1, x2,x3) по трёхмерному прямоугольному параллелепипеду и обозначается:
Пусть x1=х, x2=у, x3=z. Если функция f(x,y,z) непрерывна, область D ограниченна и определена неравенствами: x1≤х≤ x2 у1(х)≤у≤у2(х), z1(x,y)≤z≤z2(x,y), где у1(х),у2(х), z1(x,y),z2(x,y) непрерывные функции, то тройной интеграл от функции f(x,y,z), распространенный на область D, может быть вычислен по формуле:
Иногда удобно также применять формулу:
где S(x) сечение области D плоскостью х=const. При переходе от декартовых координат x,y,z к ЦИЛИНДРИЧЕСКИМ КООРДИНАТАМ φ,z, связанным с x,y,z соотношениями: х=ρcosφ, y=ρsinφ, z=z. где 0≤ρ≤+∞, 0≤φ≤2π, -∞≤z≤+∞, якобиан равен I=ρ и формула преобразования тройного интеграла к ЦИЛИНДРИЧЕСКИМ КООРДИНАТАМ ИМЕЕТ ВИД:
При переходе от декартовых координат к СФЕРИЧЕСКИМ КООРДИНАТАМ ρ,φ,θ связанными с x,y,z соотношениями: х=ρsinθcosφ, y=ρsinθsinφ, z=ρcosθ, где 0≤ρ≤+∞, 0≤φ≤2π, 0≤θ≤π. Якобиан преобразования равен: I=ρ2 sinθ и формула преобразования тройного интеграла к СФЕРИЧЕСКИМ КООРДИНАТАМ имеет вид:
Пример1: Вычислить
Пример2: Вычислить Решение: введём сферические координаты х=ρsinθcosφ, y=ρsinθsinφ, z=ρcosθ. Якобиан преобразования I=ρ2 sinθ.
ЗАДАНИЕ 1)Вычислить: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 2) Вычислить интеграл с помощью перехода к цилиндрическим или сферическим координатам. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 3) расставить пределы интегрирования в последовательности x,y,z; y,x,z; z,y,x для указанной области V. 1. V: x2+y2=r2 , z=0, z=H 2. V: 3. V: x2+y2=1, z=0, z=1 (x≥0, y≥0) 4. V: 5. V: z= 1-x2-y2, z=0 6. V: 2x+3y+4z=12, z=0, y=0, x=0. 7. V: y2+2z2=4x, x=2. 8. V: x2+y2=z2, z=1 9. V: x+y+z=1, x=0, y=0, z=0. 10. V: x2+y2=r2 , z=3, z=5. ОТВЕТЫ 1) 1. 2. 3. 1.5π 8. 4. 5.
2) 1. 1.5π 6. 2. 3. 4. 5.
1.2.2. ЛАБОРАТОРНАЯ РАБОТА 2 ВЫЧИСЛЕНИЕ ВЕЛЕЧИН ПОСРЕДСТВОМ ТРОЙНОГО ИНТЕГРАЛА ОБЬЁМ области Т определяется по формуле:
Если плотность тела переменная: γ=γ(x;y;z), то МАССА тела, занимающего область Т вычисляется по формуле:
КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ тела определяются по формулам:
При γ=I имеем:
МОМЕНТОМ ИНЕРЦИИ тела V| относительно координатных плоскостей называется, соответственно интеграл:
МОМЕНТОМ ИНЕРЦИИ относительно КООРДИНАТНЫХ ОСЕЙ: Ix= Ixy+Ixz Iy=Iyx+Iyz Iz= Izx+Izy МОМЕНТОМ ИНЕРЦИИ тела V| относительно НАЧАЛА КООРДИНАТ называется интеграл:
Используя (*) получаем: I0=Ixy+Iyz+Izx Пример1: Вычислить объем тела, ограниченного поверхностями: hz=x2+y2, z=h. Решение: данное тело ограниченно снизу параболоидом z=
Пример2: найти массу прямоугольного параллелепипеда 0≤х≤а, 0≤у≤b, 0≤z≤c, если плотность в точке (x;y;z) пропорциональна сумме координат этой точки. Решение: в данном случае γ(x;y;z)= r(x+y+z). Следовательно получим: m=
ЗАДАНИЯ 1) Найти объём тела ограниченного поверхностями: 1. 2. z=0, x=0.5(x2+y2), x2+y2+z2=4 (внутри цилиндра) 3. z=4-y2, z=y2+2, x=-1, x=2 4. z=x2+y2, z= x2+2y2, y=x, y=2x, x=1. 5. z=x2+y2, z= 2x2+2y2, y=x2, y=x. 6. x2+y2+z2=r2, x2+y2=r(r-2z), (z≥0) 7. z=x2+y2, z2=xy 8. az=x2+y2, z= 9. x+y+z=a, x+y+z=2a, x+y=z, x+y=2z 10. x2+y2+4z2=1 2) 1. Найти массу куба 0≤х≤а, 0≤у≤а, 0≤z≤а, если плотность в точке (x;y;z) есть γ(x;y;z)=x+y+z. 2. Найти массу шара радиуса R, плотность которого пропорциональна расстоянию от центра шара, причём на расстоянии единицы от шара плотность равна 2. 3. Из октана шара x2+y2+z2≤r2 (x≥0, y≥0, z≥0) вырезано тело, ограниченное координатными плоскостями 4. Определить массу тела, ограниченного поверхностями z=h, x2+y2-z2=0, если плотность в каждой точке пропорциональна аппликате этой точки. 5. Определить массу пирамиды, образованной плоскостями x+y+z=a, x=0, y=0, z=0, если плотность в каждой её точке пропорциональна аппликате этой точки. 6. Определить массу сферического слоя между поверхностями x2+y2+z2=а2 и x2+y2+z2=4а2, если плотность в каждой его точке обратно пропорциональна расстоянию точки от начала координат. 7. вычислить массу тела, ограниченного прямым круглым цилиндром радиуса R, высоты H, если его плотность в любой точке пропорциональна квадрату расстояния этой точки от центра основания цилиндра. 8. определить момент инерции относительно координатных плоскостей однородного тела ограниченного поверхностями Замечание: использовать замену x=aρcos2φ, y=bρsin2φ, z=z, (0≤φ≤2π, ρ≥0). 9. определить момент инерции относительно координатных плоскостей однородного тела ограниченного поверхностью: Замечание: использовать замену x=aρsinθcosφ, y=bρsinθsinφ, z=cρcosθ, (0≤φ≤2π, ρ≥0, 0≤θ≤π). 10. Определить момент инерции относительно координатных плоскостей однородного тела ограниченного поверхностями:
Замечание: использовать замену x=aρcosφ, y=bsinφ, z=z, (0≤φ≤2π, ρ≥0).
II 1 Найти массу куба 2 Найти массу шара радиуса R, плотность которого пропорциональна расстоянию от центра шара, причем на расстоянии единицы от шара плотность равна 2. 3 Из октана шара 4 Определить массу тела, ограниченного поверхностями z=h, 5 Определить массу пирамиды, образованной плоскостями x+y+z=a, x=0, y=0, z=0, если плотность в каждой ее точке пропорционально аппликате этой точки. 6 Определить массу сферического слоя между поверхностями 7 Вычислить массу тела, ограниченного прямым круглым цилиндром радиуса R, высоты H, если его плотность в любой точке пропорциональна расстоянию точки от начала координат. 8 Определить момент инерции относительно координатных плоскостей однородного тела ограниченного поверхностями Замечание: использовать замену 9 Определить момент инерции относительно координатных плоскостей однородного тела ограниченного поверхностью: Замечание: использовать замену 10 Определить момент инерции относительно координатных плоскостей однородного тела ограниченного поверхностями:
Поиск по сайту: |









 ДИАМЕТРОМ РАЗБИЕНИЯ области D на
ДИАМЕТРОМ РАЗБИЕНИЯ области D на частичные области Di. В каждой частичной области
частичные области Di. В каждой частичной области Di возьмём точку Mi и составим сумму :
Di возьмём точку Mi и составим сумму :

 зависит от разбиения и выбора точки MiÎDi
зависит от разбиения и выбора точки MiÎDi если для "e>0, $ d>0, что для " разбиения области D на частичные области Di с диаметром d<d и для " набора точек MiÎDi выполняется условие:
если для "e>0, $ d>0, что для " разбиения области D на частичные области Di с диаметром d<d и для " набора точек MiÎDi выполняется условие: 



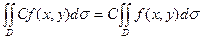 , где С=const.
, где С=const.


 , если область D ограниченна линиями:
, если область D ограниченна линиями:
 найдём координаты точек
найдём координаты точек

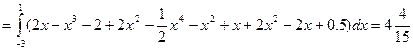

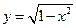 . Изменим порядок интегрирования, для чего заданную область представим в виде двух областей D1 огран. слева и справа ветвями параболы
. Изменим порядок интегрирования, для чего заданную область представим в виде двух областей D1 огран. слева и справа ветвями параболы  , ограниченную дугами окружности
, ограниченную дугами окружности 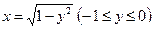 . Тогда
. Тогда 










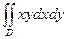 , где
, где 
 , где P ограниченна линиями
, где P ограниченна линиями 
 , где P ограниченна линиями
, где P ограниченна линиями 
 , обл Р ограниченна прямыми х=0, у=х,
, обл Р ограниченна прямыми х=0, у=х, 

 , где P ограниченна линиями
, где P ограниченна линиями 
 , где D ограниченна линиями х=2, у=х, ху=1
, где D ограниченна линиями х=2, у=х, ху=1 , где Р ограниченна линиями у=0, у=х, х+у=2
, где Р ограниченна линиями у=0, у=х, х+у=2


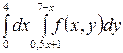
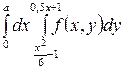
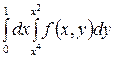






 для указанных областей S:
для указанных областей S:

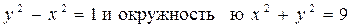 (имеется ввиду область, содержащая начало координат).
(имеется ввиду область, содержащая начало координат).

 2) 1. 1
2) 1. 1 2. 4а
2. 4а 4. -2
4. -2 5.
5.  6.
6. 
 7.
7.  8.
8. 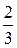
 9.
9. 
 10. 1
10. 1 связанным с прямоугольными координатами соотношением:
связанным с прямоугольными координатами соотношением:  , осуществляется по формуле:
, осуществляется по формуле:
 и двумя кривыми
и двумя кривыми 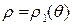 и
и  , где
, где 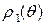
 однозначные функции при
однозначные функции при
 , то двойной интеграл вычисляется по формуле:
, то двойной интеграл вычисляется по формуле:
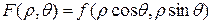 , причём сначала вычисляется интеграл
, причём сначала вычисляется интеграл  , в котором
, в котором  считается постоянным.
считается постоянным. , если D первая четверть круга
, если D первая четверть круга 


 перейти к полярным координатам и записать интеграл в виде:
перейти к полярным координатам и записать интеграл в виде:
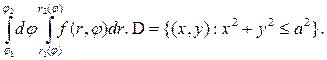










 Решение:
Решение: 
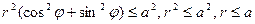

 , где D круг
, где D круг 
 , где D круг
, где D круг  .
. , где D часть кольца
, где D часть кольца  .
. , лежащая в 1-ом квадранте.
, лежащая в 1-ом квадранте. , где D круг
, где D круг 
 , где D верхний полукруг радиуса a с центром в точке (a,0)
, где D верхний полукруг радиуса a с центром в точке (a,0) , где D полукруг радиуса a с центром в начале координат, лежащей выше оси Ox.
, где D полукруг радиуса a с центром в начале координат, лежащей выше оси Ox.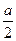 , 0).
, 0). .
. D:
D:  ,
,  .
. .
. ,
,  .
.
 .
. .
. ,
, 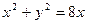 .
.












 7.
7. 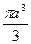
 8.
8.  9.
9. 
 10. 0
10. 0 . Если область D определена, например неравенствами
. Если область D определена, например неравенствами 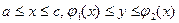 , то:
, то:
 , то:
, то:
 ,
,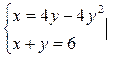 =>x=6-y
=>x=6-y => В(3,3), А(4,2) - точки пересечения
=> В(3,3), А(4,2) - точки пересечения
 (вне окружности ρ=1)
(вне окружности ρ=1) . Тогда
. Тогда 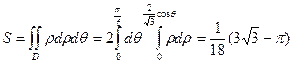
 и преобразуем наш интеграл в определённый интеграл. Из уравнения параболы находим dy=4xdx. Поэтому
и преобразуем наш интеграл в определённый интеграл. Из уравнения параболы находим dy=4xdx. Поэтому 
 .
.
 , а поэтому
, а поэтому 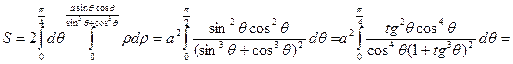

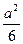





 (внутри каждой из этих кривых)
(внутри каждой из этих кривых)

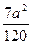

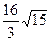












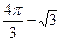


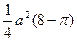

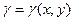 , то МАССА М пластинки выражается двойным интегралом:
, то МАССА М пластинки выражается двойным интегралом: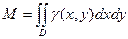
 (1)
(1) (1|)
(1|)

 (2)
(2) (2|)
(2|)



 ;
;  , где М масса пластинки, Мх, Му её статические моменты относительно осей координат.
, где М масса пластинки, Мх, Му её статические моменты относительно осей координат.
 , где S площадь области D.
, где S площадь области D. Остаётся найти
Остаётся найти  . Найдём площадь данной фигуры
. Найдём площадь данной фигуры
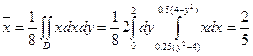
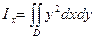
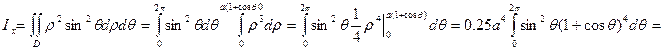
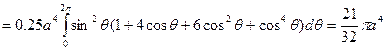
 . Вычислим интеграл I0 в полярных координатах. В полярной системе координат уравнение данной окружности представляется в виде ρ=2rcosφ. Получим:
. Вычислим интеграл I0 в полярных координатах. В полярной системе координат уравнение данной окружности представляется в виде ρ=2rcosφ. Получим: 
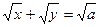 , х=0, у=0.
, х=0, у=0. , (х≥0, у≥0).
, (х≥0, у≥0). , взять перед интегралом знак “-” в следствии того, что возрастанию параметра t от 0 до
, взять перед интегралом знак “-” в следствии того, что возрастанию параметра t от 0 до  , (петля).
, (петля). , (х≥0, у≥0).
, (х≥0, у≥0). ,
,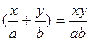 .
.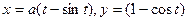 , (0≤t≤2π), у=0.
, (0≤t≤2π), у=0. относительно начала координат.
относительно начала координат. , х+у=3, у=0.
, х+у=3, у=0. относительно его большой оси.
относительно его большой оси. . Составим сумму
. Составим сумму  -это ИНТЕГРАЛЬНАЯ СУММА функции f, соответствующая данному разбиению Т и выбору точек Рj из частичных параллелепипедов Пj.
-это ИНТЕГРАЛЬНАЯ СУММА функции f, соответствующая данному разбиению Т и выбору точек Рj из частичных параллелепипедов Пj.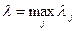 -ДИАМЕТР РАЗБИЕНИЯ Т, где
-ДИАМЕТР РАЗБИЕНИЯ Т, где  -ДИОГАНАЛЬ частичного параллелепипеда.
-ДИОГАНАЛЬ частичного параллелепипеда.


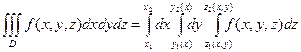
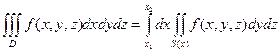

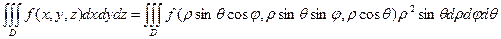
 V: z=xy, y=x, x=1, z=0
V: z=xy, y=x, x=1, z=0

 , если Т шар х2+у2+z2≤r2.
, если Т шар х2+у2+z2≤r2.

 , Т=[(x,y,z):x+y+z=1, z=0, y=0,x=0].
, Т=[(x,y,z):x+y+z=1, z=0, y=0,x=0]. ,Т:
,Т:  , x2+y2+z2≤3a2
, x2+y2+z2≤3a2 T: x2+z2=1, y=0,y=1.
T: x2+z2=1, y=0,y=1. , T: z=0, z=a, x=0, y=0, x+y=b (a>0, b>0).
, T: z=0, z=a, x=0, y=0, x+y=b (a>0, b>0). , T: y2=x, y=x2, z=xy, z=0.
, T: y2=x, y=x2, z=xy, z=0. , T: z=xy, x+y=1, z=0 (z≥0).
, T: z=xy, x+y=1, z=0 (z≥0). , T: x=0, z=0, y=0, y=h, x+z=a
, T: x=0, z=0, y=0, y=h, x+z=a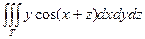 ,T: y=0, z=0,
,T: y=0, z=0, 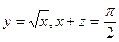
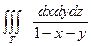 , T: x+y+z=1, z=0, x=0, y=0.
, T: x+y+z=1, z=0, x=0, y=0. , T: x+y=1, x+y=0, y=0, z=0, z=3.
, T: x+y=1, x+y=0, y=0, z=0, z=3. , G: x2+z2=1, y=0, y=1.
, G: x2+z2=1, y=0, y=1. , G:
, G: 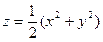 , z=2.
, z=2. , G: x2+y2+z2≤r2.
, G: x2+y2+z2≤r2. , G: x2+y2+z2≤1
, G: x2+y2+z2≤1 G: x2+y2≤2az, x2+y2+z2≤3a2
G: x2+y2≤2az, x2+y2+z2≤3a2 G: x2+y2+z2≥r2 , x2+y2+z2≤2rz
G: x2+y2+z2≥r2 , x2+y2+z2≤2rz , G:
, G:  , z≥1.
, z≥1. , 0≤z≤h.
, 0≤z≤h. , G: x2+y2+z2≤r2 , y2+z2≤x2 , x≥0.
, G: x2+y2+z2≤r2 , y2+z2≤x2 , x≥0. , G: x2+y2≤2z, 0≤z≤2.
, G: x2+y2≤2z, 0≤z≤2. , z=0, x=0, y=0 (a>0, b>0, c>0)
, z=0, x=0, y=0 (a>0, b>0, c>0) z=0
z=0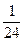 6.
6. 
 7.
7. 

 9. 0.5
9. 0.5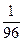 10. 3
10. 3
 7.
7. 
 8.
8. 
 9.
9. 
 10.
10. 
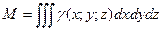


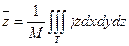



 координаты геометрического центра тяжести).
координаты геометрического центра тяжести).
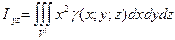 (*)
(*) .
.
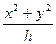 , сверху плоскостью z=h и проектируется в круг x2+y2≤h2 плоскости хОу. Используем цилиндрические координаты, в которых уравнение параболоида имеет вид z=
, сверху плоскостью z=h и проектируется в круг x2+y2≤h2 плоскости хОу. Используем цилиндрические координаты, в которых уравнение параболоида имеет вид z= 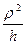 . Объём тела равен
. Объём тела равен 



 .
. , z=x2+y2
, z=x2+y2 , a>0
, a>0 (a≤c, b≤c). Найти массу этого тела, если плотность в каждой точке (x;y;z) пропорциональна аппликате этой точки.
(a≤c, b≤c). Найти массу этого тела, если плотность в каждой точке (x;y;z) пропорциональна аппликате этой точки.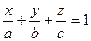 , x=0, y=0, z=0, a,b,c>0.
, x=0, y=0, z=0, a,b,c>0.
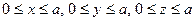 , если плотность в точке
, если плотность в точке  есть
есть 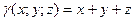 .
.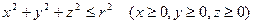 вырезано тело, ограниченное координатными плоскостями и плоскостью
вырезано тело, ограниченное координатными плоскостями и плоскостью  . Найти массу этого тела, если плотность его в каждой точке (x;y;z) пропорциональна аппликате этой точки.
. Найти массу этого тела, если плотность его в каждой точке (x;y;z) пропорциональна аппликате этой точки. , если плотность в каждой точке пропорциональна аппликате этой точки.
, если плотность в каждой точке пропорциональна аппликате этой точки. и
и  , если плотность в каждой его точке обратно пропорциональна расстоянию точки то начала координат.
, если плотность в каждой его точке обратно пропорциональна расстоянию точки то начала координат. .
. .
. .
.