 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
Основные понятия, законы и формулы
В контуре, содержащем конденсатор емкостью Взаимное соответствие между механическими и электрическими величинами, которые описывают соответствующие колебания, иллюстрируется таблицей 1. Таблица 1
7.2. Свободные незатухающие колебания. Если в контуре нет внешней ЭДС ( · Дифференциальное уравнение колебаний заряда в идеальном контуре:
где · Решение дифференциального уравнения – есть закон свободных незатухающих колебаний заряда:
где · Период свободных незатухающих колебаний в контуре:
· Сила тока в колебательном контуре изменяется по закону:
где · Напряжение на конденсаторе изменяется по закону:
где · Полная энергия идеального колебательного контура:
В контуре возникают электрические колебания, сопровождающиеся превращениями энергий электрического
7.3. Свободные затухающие колебания. Каждый реальный контур обладает активным сопротивлением, и энергия, запасенная в контуре, постепенно расходуется на нагревание. Свободные колебания будут затухающими. · Дифференциальное уравнение затухающих колебаний заряда в контуре:
где · Решение дифференциального уравнения затухающих колебаний заряда в контуре имеет вид:
где · Зная закон изменения заряда Напряжение на конденсаторе:
Сила тока в контуре:
где · Логарифмический декремент затухания электрических колебаний:
где · Добротность
В случае слабого затухания
При · Активное сопротивление контура, при котором наступает апериодический процесс, называют критическим:
7.4. Вынужденные электрические колебания. Вынужденные колебания – незатухающие колебания, возникающие под действием внешней периодически изменяющейся ЭДС
· Дифференциальное уравнение вынужденных колебаний в контуре:
или · Решение дифференциального уравнения для установившихся вынужденных колебаний заряда в контуре:
где · Амплитуда заряда в установившихся вынужденных колебаниях и разность фаз между колебаниями заряда и внешней ЭДС:
· Сила тока при установившихся колебаниях:
где
7.5. Резонанс тока – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением. · Резонансная частота для силы тока совпадает с собственной частотой контура:
· Резонансная частота для заряда и напряжения на конденсаторе:
7.6. Полное сопротивление · где · Действующие (эффективные) значения тока и напряжения:
где Амперметры и вольтметры градуируются по действующим значениям тока и напряжения. · Средняя мощность, выделяемая в цепи переменного тока:
где
Поиск по сайту: |
 7.1. Колебательный контур.
7.1. Колебательный контур. , катушку индуктивности
, катушку индуктивности 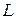 и омическое (активное) сопротивление
и омическое (активное) сопротивление  , соединенных последовательно, возникают периодические или почти периодические изменения заряда, силы тока и напряжения, рис. 12. Колебания, возникающие в таком контуре – колебательном контуре, называют электрическими (иногда электромагнитными).
, соединенных последовательно, возникают периодические или почти периодические изменения заряда, силы тока и напряжения, рис. 12. Колебания, возникающие в таком контуре – колебательном контуре, называют электрическими (иногда электромагнитными).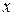

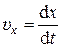
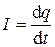


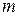
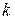






 ) и активное сопротивление
) и активное сопротивление  , то такой контур называют идеальным. Колебания в идеальном контуре являются свободными незатухающими.
, то такой контур называют идеальным. Колебания в идеальном контуре являются свободными незатухающими. или
или  ,
, – собственная частота колебаний в контуре без активного сопротивления
– собственная частота колебаний в контуре без активного сопротивления  ,
,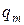 – амплитудное значение заряда на обкладках конденсатора,
– амплитудное значение заряда на обкладках конденсатора,  – начальная фаза.
– начальная фаза. (формула Томсона).
(формула Томсона). ,
,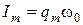 – амплитуда силы тока.
– амплитуда силы тока.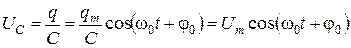 ,
, – амплитуда напряжения.
– амплитуда напряжения. .
. и магнитного
и магнитного  полей:
полей: .
. или
или  ,
, ,
,  – коэффициент затухания.
– коэффициент затухания.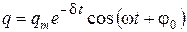 ,
, – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний;  ;
;  – частота затухающих колебаний;
– частота затухающих колебаний; 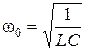 – собственная частота в отсутствии активного сопротивления.
– собственная частота в отсутствии активного сопротивления. , можно найти напряжение на конденсаторе и силу тока в контуре.
, можно найти напряжение на конденсаторе и силу тока в контуре.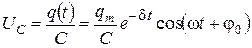 .
.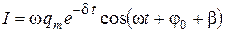 ,
, .
. ,
,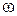 – частота затухающих колебаний.
– частота затухающих колебаний. колебательного контура:
колебательного контура: .
. добротность:
добротность: .
. вместо колебаний будет происходить апериодический разряд конденсатора.
вместо колебаний будет происходить апериодический разряд конденсатора. .
. :
: .
.
 .
. ,
, – разность фаз между колебаниями заряда и внешней ЭДС.
– разность фаз между колебаниями заряда и внешней ЭДС. ;
;  .
. ,
, – амплитуда тока, равная
– амплитуда тока, равная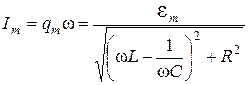 .
. .
. .
. цепи переменного тока, содержащей последовательно включенные резистор сопротивлением
цепи переменного тока, содержащей последовательно включенные резистор сопротивлением  :
: ,
, –индуктивное сопротивление;
–индуктивное сопротивление;  – емкостное сопротивление;
– емкостное сопротивление;  ;
; 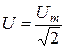 ,
, – амплитудные значения силы тока и напряжения.
– амплитудные значения силы тока и напряжения. ,
, – коэффициент мощности, равный
– коэффициент мощности, равный .
.