 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Флуктуации и временные корреляционные функции
Для того, чтобы получить информацию о динамике флуктуирующих систем, мы должны выбрать один из двух различных, но близких по физическому смыслу подходов. Мы можем анализировать флуктуирующие системы на основе частотных компонентов с разными амплитудами, получая спектр частот флуктуаций со свойствами A, <ΔA2(ν)> , где ν это частота. Однако, имеется другой, более точный метод, в котором измеряется непосредственно временная корреляционная функция флуктуаций <A(t), A(t + τ)>, где τ – корреляционное время, характеризующее флуктуации в системе. В этой главе мы будем обсуждать только эксперименты с использованием техники временных корреляционных функций, поскольку она обеспечивает более высокую точность по сравнению с техникой спектрального анализа. Иногда, для визуализации результатов мы будем иногда пользоваться спектром частот. Начнем с корреляционных функций.
Корреляционные и кросс-корреляционые функции
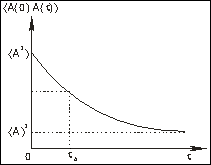
Рис. 31.2. (а) Изображение некого свойства А(t), флуктуирующего во времени относительно своего среднего <A>, равного нулю. Временная ось разбивается на ряд дискретных интервалов Δt. (б) Корреляционная функция <A(0) А(τ)>, oписывающая флуктуационный процесс, изображенный в (а). Начальное значение функции равно <A2>. Для времен значительно больших, чем корреляционное время процесса τА, корреляционная функция равна <A>2 Флуктуирующий сигнал A(t), изображенный на рисунке 31.2а, обладает следующими свойствами: свойство А для времени t всегда отлично от свойства А для времени t+Δt. Когда время τмало по сравнению с типичным временем флуктуаций переменной А(t), A(t + τ) будет близко к величине A(t). Когда величина τ увеличивается, отклонение A(t + τ) от A(t) становится более вероятным. Таким образом, можно сказать, что величина A(t + τ) коррелирует с A(t) когда τ мало, но эта корреляция теряется, когда τ становится большим по сравнению с характерным периодом флуктуаций. Мерой такой корреляции является автокорреляционная функция, определяемая как:
Если ось времени t разбить, как это сделано на рисунке 31.2а на дискретные интервалы Δt, так что t = j Δt, τ = n Δt, T =N Δt, a t+ τ = (j + n)Δt, = Δt, то интегрирование в уравнении Г10.1 можно заменить суммированием: <A>
где Аj есть значение свойства в начале j-го интервала. Мы ввели дискретизацию в описание флуктуационного процесса с тем, чтобы продемонстрировать, как корреляционная функция меняется со временем. Из рисунка 312а видно, что некоторые члены в суммах уравнений 31.2а и 31.2б отрицательны, например А3 и А4. Следовательно, в этих суммах часть вкладов будет положительна, а часть отрицательна. С другой стороны величина <A(0) A(t)> всегда положительна, так как Аj2≥ 0, и ожидается большой. Таким образом, мы можем ожидать, что корреляционная функция всегда будет постоянной, равной начальному значению для всего отрезка времен или уменьшаться от максимального значения <A2> до минимального <A>2 (рис. 31.2б). Отметим, что в большинстве практических применений корреляционная функция падает моноэкспоненциально:
где τкор есть корреляционное или релаксационное время флуктуирующего сигнала. Корреляционная функция двух свойств А и B описывается кросс-корреляционными функциями:
и
Корреляторы Рис. 31.3.Схема коррелятора для анализа флуктуирующих процессов (см. текст)
В лабораторных условиях превращение флуктуаций сигнала в корреляционную функцию выполняется с помощью прибора, называемого коррелятором (рис. 31.3). Флуктуирующий сигнал в цифровом виде передается по двум каналам: накопительному и общему каналу коррелятора. Накопитель, считает импульсы за определенный промежуток времени, Δt, длительность которого задается тактовыми кристаллическими часами. В конце этого промежутка содержимое переносится в первый регистр коррелятора. Затем коррелятор начинает считать импульсы для второго идентичного временного интервала. Этот процесс продолжается в течение всего эксперимента, так что регистры коррелятора содержат информацию о флуктуирующем сигнале за промежуток времени n Корреляционные функции поля и интенсивности
Для единичной частицы наведенный диполь p, который является источником рассеяния, определяется падающим полем Eи поляризуемостью частицы α: p= α E(31.5) Свет, излучаемый всеми индивидуально индуцируемыми диполями, собирается на детекторе, где результирующее электрическое поле зависит от относительной позиции и ориентации всех частиц в рассеивающем объеме. Типичная геометрическая картина рассеяния света представлена на рисунке 31.4. Корреляционная функция рассеивающего электрического поля, G (1)(τ), называемая корреляционной функцией первого порядка, определяется, как: G(1)(τ) = < E(t) E(t +τ) > (31.6)
Рис. 31.4.Типичнaя геометрия рассеяния света. E0 – амплитуда падающего поля; k0 и k1 – падающий и рассеивающий волновые векторы; q= k0 − k1 –волновой вектор рассеивания, определяемый углом рассеяния θ и длиной волны падающего света λ; n – показатель преломления среды
На практике, в силу квадратичной природы детектирования измеряется корреляционная функция флуктуаций интенсивности. Для интенсивности I, которая пропорциональна квадрату вектора электрического поля <E2>, нормализованная корреляционная функция, G(2)(τ), называемая корреляционной функцией второго порядка, вычисляется как: G(2)(τ) = < I(t)I(t + τ) > (31.7) Для систем, содержащих большое количество независимых источников рассеяния света, (гауссово приближение) связь между G(1) (τ)и G(2) (τ) задается соотношением: G(2)(τ) = 1 +│G (1) (τ)│2 (31.8) Корреляционные функции и частотный спектр флуктуаций
Как было упомянуто выше, частотный спектр I(ν) и корреляционная функция G(τ) полностью эквивалентны при описании динамического поведения равновесных систем, поскольку они связаны фурье-преобразованием:
где ν частота в Гц. Так, если I(ν) имеет форму Лорентца на нулевой частоте, тогда G(τ) имеет форму спадающей экспоненциальной функции с константой времени, равной обратной величине полуширины линии Лорентца. Эти простые функции верны для описания всех элементарных стохастических процессов и применимы для интерпретации поведения большинства систем, которые будут обсуждаться в дальнейшем. Простые примеры связи между корреляционной функцией и частотным спектром приведены на рисунке 31.5.
Рис. 31.5. Корреляционные функции и частотный спектр для трех простейших моделей флуктуационных процессов: (a) синусоидальная функция; (б) постоянная; (в) простейший стохастический процесс
Поиск по сайту: |
(31.1)
(31.2а)
(31.2б)
(31.3)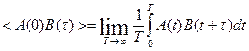
(31.4а)
(31.4б)
, где n число регистровкоррелятора, а 
называется временем выборки или временем сэмплирования, которое выбирается, как правило, в интервале времени от 2 нсек до 1сек. Время выборки должно соответствовать типичным корреляционным временам системы. Очевидно, что для быстрых процессов время выборки, берется малым, a для медленных процессов – большим.
(31.9)
