 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Співвідношення між лінійними та кутовими величинами
Лекція №1 Кінематика Елементи кінематики Рух матеріальної точки. Переміщення Швидкість. Прискорення Рух по колу Співвідношення між лінійними та кутовими величинами ü ЕЛЕМЕНТИ КІНЕМАТИКИ Завдання механіки полягає у вивченні різних рухів та встановленні їх законів, які дають можливість наперед передбачати потрібні рухи і конструювати механізми та машини. Спочатку виникла та розвивалась так звана класична механіка, основні закони якої були сформульовані Ньютоном. Вона вивчає рухи макроскопічних тіл, швидкості яких малі порівняно із швидкістю світла. Макроскопічні тіла – це звичайні тіла, що оточують нас, тобто тіла, які складаються з великої кількості молекул та атомів. Рухи тіл, швидкості яких близькі до швидкості світла, вивчаються у релятивістській механіці, основою якої є теорія відносності. Рухи мікроскопічних тіл (елементарних частинок) вивчає квантова механіка. Традиційно вивчення курсу фізики починається з класичної механіки. Це зумовлено тим, що основні її питання і методи при відповідних узагальненнях використовуються у всіх інших розділах фізики. Щодо підходу вивчення механічних рухів механіку поділяють на: § кінематику, яка вивчає змину положення тіл або їхніх частин у просторі або в часі без урахування взаємодії з іншими тілами; § динаміку – це основний розділ механіки, в якому встановлюються закони механічних рухів у зв’язку з тими механічними взаємодіями тіл, які ведуть до зміни їх механічних станів; § статику, яка вивчає умови рівноваги тіл. Її закони можна вивести із законів динаміки, тому статику розглядають як окремий випадок динаміки. Оскільки поняття простору і часу – категорії філософські, то фізика тільки встановлює властивості, притаманні саме їм. На основі дослідних даних у фізиці вважається, що властивості простору і часу не залежать від наявності матеріальних тіл, що простір - тривимірний, однорідний, неперервний та ізотропний. Однорідність простору означає, що в будь-якому його місці фізичні явища при однакових умовах відбуваються однаково. Ізотропність простору означає, що повертання системи взаємодіючих тіл на деякий кут не впливає на перебіг фізичних процесів. Класична фізика вважає, що час також однорідний, неперервний і не залежить від наявності матеріальних тіл. Об’єктами вивчення механіки є не реальні тіла в усій їх багатогранності, а ідеалізовані об’єкти – моделі- це деякий уявний образ явища, що спирається на відомі поняття і дозволяє побудувати корисну аналогію: § матеріальна точка; § абсолютно тверде тіло; § ідеальна рідина, тощо. Такі наукові абстракції дають можливість зосередити дослідження на з’ясуванні основних законів механічного руху, опускаючи другорядні деталі явищ, а також дають можливість використовувати математичний апарат при вивченні механічних рухів. За видом об’єктів дослідження механіку поділяють на: § механіку матеріальної точки; § механіку твердого тіла; § механіку суцільних середовищ (гідродинаміку, газодинаміку, теорію пружності). Матеріальна точка – найпростіший об’єкт, рух якого вивчає механіка - макроскопічне тіло, розмірами якого в даному випадку можна нехтувати, маса якого зосереджена в одній геометричній точці. Поняття про те, коли реальне тіло можна вважати матеріальною точкою, залежить не стільки від самого тіла, скільки від характеру руху, а також від змісту тих запитань, на які необхідно отримати відповіді. Абсолютні розміри тіла не відіграють ні якої ролі. Важливими є відносні розміри, тобто відношення розмірів тіла до деяких відстаней, характерних для конкретної задачі. Одне і те саме тіло в одних умовах можна вважати матеріальною точкою, в інших – ні. Так, вивчаючи рух Землі навколо Сонця, Землю можна вважати матеріальною точкою, оскільки її діаметр становить 0,0001 радіуса земної орбіти. Тіло протяжних розмірів можна замінити матеріальною точкою в тих випадках, коли важливими є не розміри і форма тіла, і його маса. Механіка однієї матеріальної точки в класичній фізиці є основою для вивчення механіки взагалі, оскільки макроскопічне тіло, або систему тіл, можна уявити як сукупність малих тіл, кожне з яких можна вважати матеріальною точкою.
ü РУХ МАТЕРІАЛЬНОЇ ТОЧКИ. ПЕРЕМІЩЕННЯ Положення точок у просторі можна характеризувати різними способами, згідно з якими можна описувати і рух точки. Координатний спосіб опису руху.При русі матеріальної точки відносно системи відліку кожному моменту часу відповідатимуть певні значення її координат. Рух матеріальної точки можна визначити, якщо відома функціональна залежність її координат від часу:
З допомогою функцій (1) можна обчислити значення координат матеріальної точки для будь-яких моментів часу. Отже, описати рух – значить задати функції (1). Лінія, яку описує матеріальна точка в просторі, називається траєкторією руху. Рівняння траєкторії Векторний спосіб опису руху.Положення матеріальної точки в просторі також можна задати за допомогою радіуса-вектора
У будь-який момент часу
Опис руху за допомогою параметрів траєкторії.Він застосовується у випадках, коли траєкторія руху є наперед відомою. Якщо траєкторія задана, то завдання зводиться до зазначення закону руху вздовж неї. Деяка точка траєкторії
Вектор переміщення.Розглянемо матеріальну точку, яка в момент часу Отже, положення точок
Відрізок, що характеризує зміну положення матеріальної точки і має напрям від початкового до наступного її положення, називатимемо вектором переміщення:
Через відповідні зміни координат рухомої точки вектор переміщення має вигляд:
Криву, яку описує кінець радіус-вектора під час руху матеріальної точки, називають годографом. Отже, траєкторія руху матеріальної точки є годографом радіус-вектора Всі тіла при певних умовах деформуються, тобто змінюють свою форму. Введемо таку модель: тіло, яке при будь-яких умовах не зазнає деформації називатимемо його абсолютно твердими. У таких тілах відстань між точками, точніше між двома його частинами, залишається сталою. Якщо під час руху форма тіла не змінюється або зазнає незначних змін, його рух можна розглядати як рух абсолютно твердого тіла. Будь-який складний рух абсолютно твердого тіла можна розкласти на два простих механічних рухи – поступальний і обертальний. Поступальним рухом тіла називатимемо такий рух, при якому пряма лінія, яка з’єднує будь-які точки тіла, з часом залишається паралельною сама собі, тобто її орієнтація у просторі не змінюється. При поступальному русі (один з найпростіших) переміщення всіх його точок однакові. Тому, знаючи рух будь-якої точки тіла, ми можемо визначити рух всіх інших його точок. Обертальним рухом називатимемо такий рух, при якому траєкторії всіх точок тіла – це концентричні кола з центром на одній прямій, яку називатимемо віссю обертання. При обертальному русі вісь обертання може знаходитись за межами тіла, що здійснює обертальний рух, а може проходити через нього. Обертання тіла навколо осі можна розкласти на поступальний рух і обертання його навколо іншої осі. Рух твердого тіла називатимемо плоским, якщо будь-яка точка тіла залишається в одній із паралельних площин.
ü ШВИДКІСТЬ. ПРИСКОРЕННЯ Основними кінематичними величинами, що характеризують рух точки, є швидкість і прискорення. Якщо матеріальна точка за певний проміжок часу
Оскільки вектор переміщення не повністю відображує характер руху, введемо поняття миттєвої швидкості - фізична величина, що визначається границею, до якої наближається середня швидкість, за умови, коли проміжок часу
Отже, миттєва швидкість – векторна величина, яка дорівнює першій похідній від вектора переміщення за часом і напрямлена по дотичній до траєкторії в бік руху. При прямолінійному русі вектор швидкості напрямлений вздовж траєкторії. Миттєва швидкість – це швидкість точки в даний момент часу або в даній точці траєкторії. Вона визначає зміну координат з часом. Вектор швидкості, як і будь-який вектор, можна виразити через його проекції на координатні осі:
Значення модуля вектора швидкості:
Якщо матеріальна точка приймає участь одразу у декількох рухах із різними миттєвими швидкостями, то повна швидкість точки дорівнюватиме векторній сумі окремих швидкостей. Це так зване правило додавання швидкостей, яке ввів ще Галілей, воно є наслідком принципу незалежності рухів:
Якщо траєкторія руху матеріальної точки і рівняння її руху відомі, то значення миттєвої швидкості визначається першою похідною від шляху
На практиці часто використовують скалярну середню величину швидкості, яка визначається відношенням пройденого шляху до часу проходження:
Рух, при якому величина і напрям вектора швидкості з часом не змінюється, називають рівномірним і прямолінійним. Швидкість в СІ вимірюють такими одиницями:
Але на практиці користуються км/год, у морській справі – вузлами (1 вузол = 1 морській милі/год = 1,853 км/год), у реактивній авіації – махами (1 М = 1200 км/год). Існують спеціальні прилади, за допомогою яких безпосередньо вимірюють швидкість руху тіл. Наприклад, швидкість руху автомобіля вимірюють спідометром. Зверніть увагу на те, що введене поняття середньої швидкості – це не середнє арифметичне, а середнє за часом. Якщо за проміжок часу
Якщо б замість При русі матеріальної точки її швидкість у загальному випадку може змінюватися як за величиною, так і за напрямом. Зміну швидкості за часом характеризують фізичною величиною, яку називають прискоренням. Повна зміна швидкості
Величину відношення зміни швидкості
Оскільки середнє прискорення не повністю відображує характер руху матеріальної точки, то вводять ще поняття миттєвого прискорення, тобто прискорення в даний момент часу або прискорення в даній точці траєкторії. Миттєве значення прискорення визначається границею, до якої прямує величина
Зробимо паралельне перенесення векторів § § За означенням миттєве прискорення:
де Тангенціальне прискорення Нормальне Модуль і напрям повного прискорення в даній точці траєкторії:
де § § § При русі в один і той же бік по прямолінійній траєкторії швидкість змінюється лише за модулем. Відповідно прискорення повинно визначатися значенням
ü РУХ ПО КОЛУ Розглянемо, як окремий випадок криволінійного руху
Поділивши обидві частини на
Звідси маємо:
Оскільки при
Обертання тіла із сталою кутовою швидкістю називатимемо рівномірним. Нерівномірне обертання тіла характеризуватиме за допомогою кутового прискорення. Якщо за малий проміжок часу
З урахуванням (26):
При обертальному русі всі точки твердого тіла мають однакові кутові швидкості і кутове прискорення. Кутову швидкість і кутове прискорення вимірюють:
ü СПІВВІДНОШЕННЯ МІЖ ЛІНІЙНИМИ ТА КУТОВИМИ ВЕЛИЧИНАМИ Встановимо співвідношення між лінійною і кутовою швидкостями та лінійним і кутовим прискоренням. Довжина дуги
Поділимо на
На основі формул (25) та (31) отримаємо, що нормальне прискорення:
Тангенціальне прискорення:
З рівнянь (32) та (33) видно, що як нормальне так і тангенціальне прискорення пропорційне відстані від осі обертання
Отже, знаючи кутову швидкість і кутове прискорення тіла, що обертається, а також відстань від осі обертання, можна визначити величину і напрям прискорення будь-якої точки тіла. Оскільки відношення тангенціального прискорення до нормального:
При обертальному русі кутова швидкість і кутове прискорення визначаються однозначно тоді, коли відоме розташування в просторі осі обертанні і вказано напрям обертання навколо неї. Оскільки лінійна швидкість і лінійне прискорення – векторні величини, а крім того між величинами
В разі, коли орієнтація осі обертання з часом не змінюється, вектор кутового прискорення
На Рис.8 показано розташування векторів Обертання характеризується також періодом обертання
Оскільки за період
Рекомендована література: 1. Савельев И.В. Курс общей физики. Т.1. Механика. Молекулярная физика. – М.: Наука, 1987. – 432 с. 2. Бушок Г.Ф., Левандовський В.В., Півень Г.Ф. Курс фізики. 1 кн. Фізичні основи механіки. Електрика і магнетизм. – К.: Либідь, 2001. – 448 с. 3. Кучерук І.М., Горбачук І.Т. Загальна фізика. 1 кн. Фізичні основи механіки. Молекулярна фізика і термодинаміка. – К.: Вища шк., 1995. – 431 с. 4. Зисман Г.А., Тодес О.М. Курс общей физики. Т.1. Механика. Молекулярная физика. – М.: Наука, 1974. 5. Гершензон Е.М., Малов Н.Н. Курс общей физики. Механика. - М.: Просвещение, 1987. – 307 С. 6. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Т.1.– М.: Мир. 7. Киттель Ч., Найт У., Рудерман М. БКФ. Механика. - М.: Наука, 1975. – 480 С. 8. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш. шк.., 1989. – 608 с. 9. Кузьмичев В.Е. Законы и формулы физики. Справочник. – Киев: Наук. думка, 1989. – 864 с. 10. Иродов И.Е. Основы классической механики. – М.: Высш. шк. 11. Голдстейн Г. Классическая механика. 12. Савельев И.В. Курс физики. В 3-х томах. Т.1. Механика. Молекулярная физика.– М.: Наука, 1989. – 352 с.
Поиск по сайту: |
 ,
,  ,
, 
 в явній формі можна дістати з системи рівнянь (1). Якщо траєкторія - пряма лінія, то рух називають прямолінійним; якщо ж це крива лінія, то, рух – криволінійний. Найпростішим прикладом криволінійного руху є рух матеріальної точки по колу. При цьому характер її траєкторії залежить від системи відліку. Так, точки обода колеса, що котиться по горизонтальній площині, матиме різні траєкторії відносно осі обертанні і відносно поверхні площини. У першому випадку це буде коло, у другому – циклоїда. Довжину траєкторії, яку проходить точка за проміжок часу, називатимемо шляхом.
в явній формі можна дістати з системи рівнянь (1). Якщо траєкторія - пряма лінія, то рух називають прямолінійним; якщо ж це крива лінія, то, рух – криволінійний. Найпростішим прикладом криволінійного руху є рух матеріальної точки по колу. При цьому характер її траєкторії залежить від системи відліку. Так, точки обода колеса, що котиться по горизонтальній площині, матиме різні траєкторії відносно осі обертанні і відносно поверхні площини. У першому випадку це буде коло, у другому – циклоїда. Довжину траєкторії, яку проходить точка за проміжок часу, називатимемо шляхом.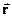 , який проводять з початку системи координат до матеріальної точки. Цей спосіб є більш раціональним. При русі матеріальної точки в загальному випадку величина і напрям
, який проводять з початку системи координат до матеріальної точки. Цей спосіб є більш раціональним. При русі матеріальної точки в загальному випадку величина і напрям 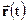
 проекції радіуса-вектора
проекції радіуса-вектора 
 +
+ 
 +
+ 

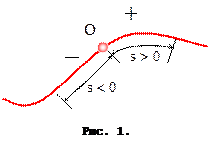 де
де  приймається за початкову, а будь-яка інша характеризується відстанню
приймається за початкову, а будь-яка інша характеризується відстанню  вздовж неї від початкової точки, встановлюється на траєкторії додатній і від’ємний напрямок відліку (як на осі координат) (Рис.1). Цей шлях не є вектором, він є скаляром, і не має певного напряму в просторі. В цьому випадку рух описується формулою:
вздовж неї від початкової точки, встановлюється на траєкторії додатній і від’ємний напрямок відліку (як на осі координат) (Рис.1). Цей шлях не є вектором, він є скаляром, і не має певного напряму в просторі. В цьому випадку рух описується формулою: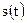
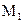 , радіус-вектор якої
, радіус-вектор якої  ) матеріальна точка буде знаходитись в точці
) матеріальна точка буде знаходитись в точці 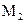 , радіус-вектор якої
, радіус-вектор якої  .
.
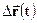 =
= 
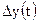

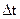 здійснила переміщення
здійснила переміщення 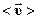 =
= 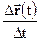
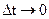 :
: =
= 
 =
=  =
= 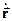



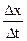 =
=  =
=  ,
,  ,
, 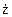
 =
= 
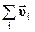 .
.
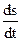
 =
= 
 =
=  .
.
 швидкість руху була
швидкість руху була  , а за інтервал
, а за інтервал  вона дорівнювала
вона дорівнювала  , то середня за часом швидкість:
, то середня за часом швидкість: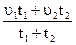 .
.
 і
і  , то дістали б швидкість, усереднену за відстанню. Таким поняттям користуються у гідродинаміці. Отже, середня швидкість – це, швидкість усереднена за часом.
, то дістали б швидкість, усереднену за відстанню. Таким поняттям користуються у гідродинаміці. Отже, середня швидкість – це, швидкість усереднена за часом. за час
за час 
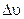 до часу
до часу  =
= 
 =
= 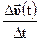 =
=  =
=  , або
, або 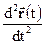 =
= 
 =
= 
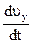




 Якщо матеріальна точка рухається із сталим прискоренням, то такий рух називають рівнозмінним. Прискорення – векторна величина. Вектор напрямлений у той бік, куди напрямлений вектор зміни швидкості
Якщо матеріальна точка рухається із сталим прискоренням, то такий рух називають рівнозмінним. Прискорення – векторна величина. Вектор напрямлений у той бік, куди напрямлений вектор зміни швидкості  =
= 
 Розглянемо випадок, коли траєкторія руху матеріальної точки – плоска крива лінія (Рис.3). Нехай у момент часу
Розглянемо випадок, коли траєкторія руху матеріальної точки – плоска крива лінія (Рис.3). Нехай у момент часу  траєкторії мала швидкість
траєкторії мала швидкість  , а в момент часу
, а в момент часу 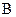 траєкторії – швидкість
траєкторії – швидкість  .
. - вздовж вектора
- вздовж вектора  - вздовж нормалі до вектора
- вздовж нормалі до вектора  =
=  +
+ 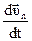 =
=  +
+ 
 =
= 
 =
= 
 - кут між вектором прискорення і дотичною до траєкторії руху матеріальної точки в даний момент часу (Мал.1.4). Тангенціальне і нормальне прискорення можуть бути ознаками різних рухів:
- кут між вектором прискорення і дотичною до траєкторії руху матеріальної точки в даний момент часу (Мал.1.4). Тангенціальне і нормальне прискорення можуть бути ознаками різних рухів: =
=  - рівнозмінний рух;
- рівнозмінний рух; ,
, 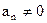 - рівномірний криволінійний рух;
- рівномірний криволінійний рух; =
=  - похідної модуля швидкості за часом. При рівномірному русі по криволінійній траєкторії
- похідної модуля швидкості за часом. При рівномірному русі по криволінійній траєкторії  рівномірний рух матеріальної точки по колу радіуса
рівномірний рух матеріальної точки по колу радіуса 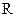 з центром
з центром  і трикутник зі сторонами
і трикутник зі сторонами  ,
, 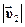 ,
,  - подібні. З їхньої подібності маємо:
- подібні. З їхньої подібності маємо: =
=  або
або 
 =
= 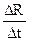 або
або  =
= 
 =
= 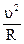 .
.
 , то
, то  і вектор
і вектор 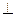
 При обертальному русі твердого тіла навколо нерухомої осі всі його точки описують кола, центри яких лежать на осі обертання (Рис.6). Проведемо через вісь обертання дві площини1 і2. Одну з них (2) жорстко зв’яжемо з тілом, а другу (1) вважатимемо нерухомою. Обертання тіла навколо осі можна задати за допомогою кута
При обертальному русі твердого тіла навколо нерухомої осі всі його точки описують кола, центри яких лежать на осі обертання (Рис.6). Проведемо через вісь обертання дві площини1 і2. Одну з них (2) жорстко зв’яжемо з тілом, а другу (1) вважатимемо нерухомою. Обертання тіла навколо осі можна задати за допомогою кута  між цими площинами. Якщо за проміжки часу
між цими площинами. Якщо за проміжки часу 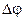 , то границю, до якої прямує відношення
, то границю, до якої прямує відношення 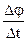 при
при  =
=  =
=  .
.
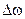 , то границя, до якої прямує відношення
, то границя, до якої прямує відношення 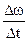 при
при 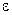 =
=  =
= 

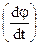 =
=  =
= 
 =
=  ;
;  =
= 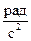
 , яку описує точка, що знаходиться на відстані
, яку описує точка, що знаходиться на відстані 

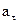 =
= 
 =
= 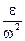
 є однаковим для всіх точок тіла, то вектор повного прискорення для всіх точок тіла утворює з радіусом, проведеним до цієї точки, один і той самий кут
є однаковим для всіх точок тіла, то вектор повного прискорення для всіх точок тіла утворює з радіусом, проведеним до цієї точки, один і той самий кут  (Рис.7).
(Рис.7). Вектор кутової швидкості зображують відрізком прямої, яка збігається з віссю обертання. Довжина цієї прямої в певному масштабі виражає величину кутової швидкості. Цей зв’язок умовились встановлювати за правилом правого гвинта: вектор кутової швидкості напрямлений вздовж осі обертання в бік поступального руху гвинта, коли його обертати за напрямом обертання (Рис.8). Такий вектор називають осьовим або аксіальним. Оскільки кутова швидкість
Вектор кутової швидкості зображують відрізком прямої, яка збігається з віссю обертання. Довжина цієї прямої в певному масштабі виражає величину кутової швидкості. Цей зв’язок умовились встановлювати за правилом правого гвинта: вектор кутової швидкості напрямлений вздовж осі обертання в бік поступального руху гвинта, коли його обертати за напрямом обертання (Рис.8). Такий вектор називають осьовим або аксіальним. Оскільки кутова швидкість  – вектор, зміна кутової швидкості
– вектор, зміна кутової швидкості  є також вектором. Отже, кутове прискорення
є також вектором. Отже, кутове прискорення  – також вектор, який збігається за напрямом з вектором
– також вектор, який збігається за напрямом з вектором 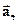 =[
=[ 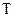 і частотою обертання
і частотою обертання  . Період обертання
. Період обертання 
 :
: =
=