 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теоретическое введение. Изучение зависимости скорости звука в воздухе от температуры
Изучение зависимости скорости звука в воздухе от температуры резонансным методом и определение отношения теплоемкостей Ср/Сv
Цель работы: определение зависимости скорости звука в воздухе от температуры и определение Ср/Сv для воздуха. Приборы и инструменты: экспериментальная установка ФПТ1–7. Теоретическое введение Распространение звуковой волны в газе происходит адиабатически. Сжатия и разрежения в газе сменяют друг друга так быстро, что теплообмен между слоями газа, имеющими разные температуры, не успевает произойти. Адиабатический процесс описывается уравнением Пуассона:
где: γ = Ср/Сv – показатель адиабаты(постоянная Пуассона). Скорость звука в газах определяется формулой: c= где: Т–температура газа, μ – молярная масса газа. Из этой формулы можно получить выражение, которое определяет коэффициент Пуассона:
Таким образом, для определения показателя адиабаты достаточно измерить температуру газа и скорость распространения звука в нем. Для этого в данной работе применяется экспериментальный метод, основанный на использовании явления звукового резонанса (стоячая волна) в трубке с закрытыми торцами. Звуковая волна, распространяющаяся вдоль трубы, испытывает многократные отражения от ее торцов. Следовательно, звуковые колебания в трубе являются наложением всех отраженных волн и очень сложны. Картина упрощается, если длина трубы L равна целому числу полуволн: L = n где: Скорость звука определяется по формуле: c = где: c = Таким образом, измеряя частоту, соответствующую резонансу, можно определить скорость звука. Это выполняется следующим образом. При постоянной длине трубы изменяется частота звуковых колебаний. Для k+1 последовательных резонансов имеем: L = Следовательно, для частоты резонансов получается:
Из последнего соотношения видно, что частота резонанса пропорциональна его номеру. Таким образом, скорость звука можно определить с помощью углового коэффициента графика зависимости частоты от номера резонанса.
Поиск по сайту: |
 = const, (1)
= const, (1) , (2)
, (2) =
=  c2. (3)
c2. (3) , (4)
, (4)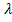 – длина волны звука в трубе, n – любое целое число. В этом случае волна, отраженная от торца трубы, совпадает по фазе с падающей. Совпадающие по фазе волны усиливают друг друга. Амплитуда звуковых колебаний при этом резко возрастает – наступает резонанс, возникает стоячая волна.
– длина волны звука в трубе, n – любое целое число. В этом случае волна, отраженная от торца трубы, совпадает по фазе с падающей. Совпадающие по фазе волны усиливают друг друга. Амплитуда звуковых колебаний при этом резко возрастает – наступает резонанс, возникает стоячая волна. , (5)
, (5) – частота звуковых колебаний. Подставляя (5) в формулу (4), получаем:
– частота звуковых колебаний. Подставляя (5) в формулу (4), получаем: , (6)
, (6) (7)
(7) (8)
(8)