 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
К л а с и ф і к а ц і я с и л, щ о д і ю т ь н а м а т е р і-Стр 1 из 3Следующая ⇒
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ „ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”
МЕТОДИЧНІ ВКАЗІВКИ до лабораторних занять з курсу “Теоретична механіка ” Для студентів спеціальностей ФТ-факультету Комп’ютерний лабораторний практикум Лабораторна робота 4 ДОСЛІДЖЕННЯ ПРЯМОЛІНІЙНИХ КОЛИВАНЬ МАТЕРІАЛЬНОЇ ТОЧКИ
Затверджено редакційно-видавничою радою університету, протокол № ____ від ____
Харків НТУ “ХПІ” 2012 Методичні вказівки до лабораторних занять з курсу “Теоретична механіка” для студентів спеціальностей ФТ-факультету. Комп’ютерний лабораторний практикум. Лабораторна робота 4 «Дослідження прямолінійних коливань матеріальної точки» // Укл. Д.В. Лавінський. – Харків: НТУ “ХПІ”, 2012. – с .
Укладач: Д.В. Лавінський
Рецензент В.М. Адашевський
Кафедра теоретичної механіки Мета, об’єкт, предмет та методи досліджень: Метою роботи є дослідження закономірностей механічних коливань матеріальної точки. Об’єктом дослідженьє матеріальна точка, яка здійснює коливальний рух.Предметомє коливальний рух матеріальної точки. Методи досліджень містять: аналітичне та комп’ютерне моделювання.
Теоретичний матеріал Серед багатьох різноманітних видів руху, які можуть здійснювати матеріальні об’єкти, особливе місце займають таки, при яких матеріальні об’єкти через однакові проміжки часу займають одні та ти ж самі положення у просторі, або рух відбувається подібним чином. Такі види руху називають механічними коливаннями. Коливання настільки поширені у природі та в техніці, що вивчення їхніх закономірностей має самостійне значення. Різні по своїй фізичній природі коливальні явища мають однаковий математичний опис. Дослідження коливань матеріальної точки є прикладом вивчення загальних закономірностей коливань. К л а с и ф і к а ц і я с и л, щ о д і ю т ь н а м а т е р і- а л ь н у т о ч к у.Серед сил, діючих на матеріальну точку, особливе місце займають поновлюючи сили, що прагнуть повернути точку в положення рівноваги. Вони залежать від величини відхилення точки від положення рівноваги і направлені убік, протилежний відхиленню. Саме ці сили надають руху точки коливальний характер. На рис. 1 наведено два приклади, в 1-му з яких поновлююча сила
а) б) Рисунок 1. Приклади виникнення поновлюючих сил: а) сила пружності; б) сила Архімеда
На рухомі тіла зазвичай діють ще й сили опору, які залежать від швидкості руху. Крім того, можуть також діяти збуджуючи сили, які будучи прикладеними до механічної системи , викликають її коливання. Прямолінійні коливання матеріальної точки мають місце, коли траєкторією руху точки є пряма. Якщо при цьому поновлюючи сили є пропорційними величині відхилення точки від положення рівноваги, а сили опору – пропорційними швидкості точки, то коливання будуть лінійними (малими). Д и ф е р е н ц і а л ь н е р і в н я н н я м а л и х п р я м о- л і н і й н и х к о л и в а н ь м а т е р і а л ь н о ї т о ч к и.Нехай на точку
Рисунок 2. Розрахункова модель прямолінійних коливань матеріальної точки Спроектуємо цю векторну рівність на вісь
Якщо розділити обидві частини цього рівняння на масу
де Власні коливання(вільні коливання у середовищі без опору) –це коливання матеріальної точки, які відбуваються під дією лише поновлюючої сили. Такі коливання описують однорідним диференціальним рівнянням, яке можна отримати з рівняння (3), якщо покласти
Характеристичне рівняння диференціального рівняння власних коливань має чисто уявні корні, тому загальний розв’язок (4) запишемо у вигляді
де
В решті одержимо закон руху точки при власних коливаннях
розв’язок якого можна перетворити до більш зручного вигляду, якщо ввести наступні позначення:
Таким чином, власні коливання матеріальної точки є гармонійними; Власні коливання будуть відбуватися у системі, зображеної на рис. 3,б. Вантаж
а) б) Рисунок 3. Власні коливання матеріальної точки: а) розрахункова модель власних коливань; б) графік залежності від часу координати точки при власних коливаннях
Диференціальне рівняння руху вантажу має вигляд
Якщо розглянути стан рівноваги, то можна встановити, що Затухаючі коливання(вільні коливання за наявності в’язкого опору)– цеокремий випадокруху матеріальної точки під дією поновлюючої сили і сили опору. Диференціальне рівняння такого руху одержуємо з виразу (3) при
Його характеристичне рівняння має корені
Рисунок 4. Графік залежності від часу координати точки при затухаючих коливаннях В и п а д о к м а л о г о о п о р у. Мають місце затухаючі коливання(
де
Рисунок 5. Графіки залежності від часу координати точки при аперіодичному русі за різних початкових умов В и п а д о к к р и т и ч н о г о о п о р у. Він має місце,коли
В и п а д о к в е л и к о г о о п о р у.Він має місце,коли
У двох останніх випадках рух точки втрачає коливальний характер і стає аперіодичним. Залежно від величини і направлення початковій швидкості графік коливань має вид однієї з трьох кривих, приведених на рис. 5. Константи Вимушені коливання– це коливання, які здійснює матеріальна точка під дією поновлюючої сили, а також сил опору і збудження. Їх описують неоднорідним диференціальним рівнянням (3), яке має загальний розв’язок у вигляді
де
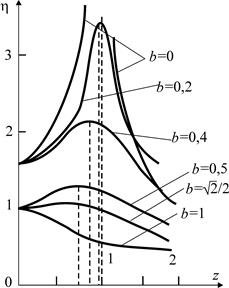
Параметрична залежність коефіцієнту динамічності від коефіцієнту розладу та безрозмірного коефіцієнту в’язкості отримала назву амплітудно-частотної характеристики(АЧХ).На рис. 6 наведено криві АЧХ для різних значень безрозмірного коефіцієнта в’язкості
Криві залежності зрушення фаз від коефіцієнта розладу
Рисунок 6. АЧХ при різних коефіцієнтах в’язкості
Диференціальне рівняння вимушених коливань у середовищі без опору одержимо з виразу (3) при
а також коефіцієнт динамічності
Резонанс – це явище значного зростання амплітуди коливань, яке виникає у разі збігу частоти збуджуючої сили та власної частоти коливань. Тоді при відсутності в’язкого опору закон резонансних коливань має вигляд
Графік таких коливань приведено на рис. 7. Таким чином, при резонансі розмахи коливань зростають з часом необмежено, причому збільшення розмахів пропорційне часу.
Рисунок 7. Графік залежності від часу координати точки при резонансі за відсутності в’язкого опору Биття – це явище періодичної зміни у часі амплітуди коливання, яке виникає при складанні двох гармонічних коливань із частотами, що відрізняються на малу величину. Биття виникають внаслідок того, що різниця фаз між двома коливаннями увесь час змінюється так, що обидва коливання опиняються у деякий момент часу у фазі, через деякий час у протифазі, потім знов у фазі і т.д. Відповідно амплітуда результуючого коливання періодично досягає то максимуму (він рівний сумі амплітуд коливань), то мінімуму (він рівний різниці цих амплітуд).
Рисунок 7. Графік залежності від часу координати точки при биттях Вимушені коливання це фактично складання власних (або вільних) коливань із частотою
Поиск по сайту: |
 – це сила пружності деформованої пружини, а у 2-му – рівнодійна сили ваги
– це сила пружності деформованої пружини, а у 2-му – рівнодійна сили ваги  і сили Архімеда
і сили Архімеда  (
(  ). В обох випадках початок відліку координати
). В обох випадках початок відліку координати  прийнято у положенні рівноваги тіла. Дані тіла рухаються поступально, тому рух кожного з них еквівалентний руху матеріальної точки.
прийнято у положенні рівноваги тіла. Дані тіла рухаються поступально, тому рух кожного з них еквівалентний руху матеріальної точки.
 масою
масою  діє поновлююча сила
діє поновлююча сила  , а початкова швидкість точки направлена уздовж прямої
, а початкова швидкість точки направлена уздовж прямої  . (1)
. (1)
 , де
, де  – коефіцієнт пропорційності,
– коефіцієнт пропорційності,  ; сила опору –
; сила опору –  , де
, де  – коефіцієнт в’язкості
– коефіцієнт в’язкості  ; збуджуюча сила –
; збуджуюча сила –  , де
, де  – амплітуда збуджуючої сили
– амплітуда збуджуючої сили  ,
,  – її частота. Тоді одержимо наступне диференціальне рівняння руху точки
– її частота. Тоді одержимо наступне диференціальне рівняння руху точки  . (2)
. (2) , (3)
, (3) – власна (кругова або циклічна) частота коливань;
– власна (кругова або циклічна) частота коливань;  – коефіцієнт затухання;
– коефіцієнт затухання; 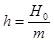 . Рівняння (3) – це диференціальне рівняння вимушених коливань точки за наявності в’язкого опору, з нього можна одержати більш прості диференціальні рівняння, які відповідатимуть окремим випадкам коливань.
. Рівняння (3) – це диференціальне рівняння вимушених коливань точки за наявності в’язкого опору, з нього можна одержати більш прості диференціальні рівняння, які відповідатимуть окремим випадкам коливань.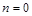 та
та 
 . (4)
. (4) , (5)
, (5) і
і  – постійні, що визначають з початкових умов
– постійні, що визначають з початкових умов . (6)
. (6) , (7)
, (7) . (8)
. (8) . (9)
. (9) – амплітуда коливань,
– амплітуда коливань,  – фаза коливань;
– фаза коливань;  – початкова фаза; власні коливання відбуваються з періодом
– початкова фаза; власні коливання відбуваються з періодом  . Частота і період гармонійних коливань залежать від маси точки і коефіцієнта пропорційності поновлюючої сили, але не залежать від початкових умов. Цю властивість вільних коливань називають ізохронністю. Амплітуда і початкова фаза залежать як від параметрів системи
. Частота і період гармонійних коливань залежать від маси точки і коефіцієнта пропорційності поновлюючої сили, але не залежать від початкових умов. Цю властивість вільних коливань називають ізохронністю. Амплітуда і початкова фаза залежать як від параметрів системи  і сила пружності
і сила пружності 

 . (10)
. (10)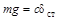 . Далі, виконуючи відповідні перетворення, одержимо диференційне рівняння подібне (4). Тобто, наявність сталої сили (в даному випадку – сили ваги) не впливає на характер коливального процесу, а призводить до зсуву центра коливань. Графік власних коливань наведено на рис. 3,а.
. Далі, виконуючи відповідні перетворення, одержимо диференційне рівняння подібне (4). Тобто, наявність сталої сили (в даному випадку – сили ваги) не впливає на характер коливального процесу, а призводить до зсуву центра коливань. Графік власних коливань наведено на рис. 3,а. . (11)
. (11) . Характер руху точки істотно залежить від співвідношення величин
. Характер руху точки істотно залежить від співвідношення величин  і
і 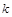 . Розглянемо три можливі випадки цього співвідношення.
. Розглянемо три можливі випадки цього співвідношення.
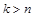 ), якіописують наступним рівнянням:
), якіописують наступним рівнянням: , (12)
, (12) – умовна амплітуда;
– умовна амплітуда;  – частота затухаючих коливань;
– частота затухаючих коливань;  – початкова фаза затухаючих коливань, графік яких наведено на рис. 4. Затухаючі коливання не є періодичними, але проміжок часу між двома послідовними максимальними відхиленнями точки від положення рівноваги в одну й ту ж сторону залишається незмінним. Цю величину називають умовним періодом затухаючих коливань
– початкова фаза затухаючих коливань, графік яких наведено на рис. 4. Затухаючі коливання не є періодичними, але проміжок часу між двома послідовними максимальними відхиленнями точки від положення рівноваги в одну й ту ж сторону залишається незмінним. Цю величину називають умовним періодом затухаючих коливань  . Швидкість загасання коливань характеризують відношенням величин двох послідовних максимальних відхилень точки від положення рівноваги в одну й ту ж сторону. Це відношення називаютьдекрементом коливань
. Швидкість загасання коливань характеризують відношенням величин двох послідовних максимальних відхилень точки від положення рівноваги в одну й ту ж сторону. Це відношення називаютьдекрементом коливань  . Натуральний логарифм цієї величини – так званий логарифмічний декремент коливань.
. Натуральний логарифм цієї величини – так званий логарифмічний декремент коливань.
 , тобто корені характеристичного рівняння є дійсними числами, рівними та від’ємними, а загальний розв’язок диференціального рівняння прямолінійного руху має вигляд
, тобто корені характеристичного рівняння є дійсними числами, рівними та від’ємними, а загальний розв’язок диференціального рівняння прямолінійного руху має вигляд . (13)
. (13) , тобто корені характеристичного рівняння дійсні, різні та від’ємні, а загальний розв’язок диференціального рівняння має вигляд
, тобто корені характеристичного рівняння дійсні, різні та від’ємні, а загальний розв’язок диференціального рівняння має вигляд . (14)
. (14)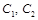 визначають, використовуючи початкові умови руху.
визначають, використовуючи початкові умови руху. (15)
(15)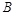 – амплітуда вимушених коливань,
– амплітуда вимушених коливань,  – зрушення фаз. Аналізуючи формули (15), можна зробити висновок, що вимушені коливання є незатухаючими, а їхні частота та період дорівнюють частоті та періоду сили збудження. Амплітуда вимушених коливань залежить від власної частоти, частоти збуджуючої сили та від коефіцієнту затухання, а значить від коефіцієнту в’язкості
– зрушення фаз. Аналізуючи формули (15), можна зробити висновок, що вимушені коливання є незатухаючими, а їхні частота та період дорівнюють частоті та періоду сили збудження. Амплітуда вимушених коливань залежить від власної частоти, частоти збуджуючої сили та від коефіцієнту затухання, а значить від коефіцієнту в’язкості 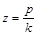 , безрозмірний коефіцієнт в’язкості –
, безрозмірний коефіцієнт в’язкості – 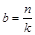 , коефіцієнт динамічності –
, коефіцієнт динамічності – 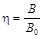 , де
, де  – статичне відхилення точки під дією сили, яка дорівнює амплітуді
– статичне відхилення точки під дією сили, яка дорівнює амплітуді  . Перейдемо у другій формулі (15) до коефіцієнту динамічності та одержимо, що
. Перейдемо у другій формулі (15) до коефіцієнту динамічності та одержимо, що . (16)
. (16) . Так само можна перетворити й третю формулу (15) та одержати залежність зрушення фаз від коефіцієнта розладу та безрозмірного коефіцієнта в’язкості
. Так само можна перетворити й третю формулу (15) та одержати залежність зрушення фаз від коефіцієнта розладу та безрозмірного коефіцієнта в’язкості . (17)
. (17) для різних значень коефіцієнта
для різних значень коефіцієнта  зрушення фаз дорівнює
зрушення фаз дорівнює  при будь-яких значеннях
при будь-яких значеннях  .
.

 , (18)
, (18) . (19)
. (19) . (20)
. (20)

 ). Тоді результуючі коливання, тобто биття, будуть здійснюватися за законом:
). Тоді результуючі коливання, тобто биття, будуть здійснюватися за законом: (21)
(21)  (22)
(22)  ,
, 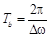 . (23)
. (23)