 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Швидкості та прискорення точок тіла, що обертається
Як було відзначено раніше, прямі, проведені в тілі паралельно осі обертання (наприклад, пряма mm' на рис. 2.2), здійснюють поступальний рух, тобто, швидкості та прискорення усіх точок кожної такої прямої будуть однакові. Отже, для вивчення кінематичних характеристик точок тіла досить визначити відповідні величини для точок перетину, проведеного перпендикулярно осі обертання. Траєкторіями усіх точок, що не лежать на осі обертання, є кола, площини яких перпендикулярні осі обертання, а центри лежать на цій осі. Розглянемо яку-небудь точку М тіла, що знаходиться на відстані h від осі обертання (рис. 2.2). Якщо за час dt відбувається елементарне обертання тіла на кут dj, то точка М при цьому здійснює по своїй траєкторії елементарне переміщення
Таким чином, алгебраїчне значення величини швидкості точки твердого тіла, що обертається навколо нерухомої осі, дорівнює добутку кутової швидкості тіла на відстань від цієї точки до осі обертання.Вектор швидкості Вектори швидкостей усіх точок перерізу, перпендикулярного осі обертання, будуть розташовуватися в його площині, утворюючи поле швидкостей, вид якого зображений на рис. 2.4. Відзначимо, що: 1) вектори швидкостей точок перпендикулярні прямим, що з'єднують точки з віссю обертання, і спрямовані у бік обертання тіла (дугової стрілки w); 2) модулі швидкостей точок тіла, що обертається, пропорційні їх відстаням від осі обертання. Швидкість Для знаходження прискорення точки М скористаємося формулами
Дотична складова прискорення Повне прискорення точки М буде
Відхилення вектора
Рис. 2.6
Зазначимо, що при обчисленні кінематичних характеристик різних точок тіла, що обертається, в формули (2.12), (2.13) для даного моменту часу будуть підставлятися тіж самі значення величин Поле прискорень точок тіла показано на рис. 2.6. Приведемо також векторні вирази швидкості та прискорення точки тіла, що обертається. Нехай тіло здійснює обертальний рух і в даний момент часу відомі характеристики його руху З побудови на рис. 2,7,а випливає, що вектор швидкості будь-якої точки тіла, що обертається, дорівнює векторному добутку вектора кутової швидкості тіла на радіус-вектор цієї точки(формула Ейлера):
Модуль цього вектора
а) б) Рис. 2.7
Вектор прискорення точки М визначимо як похідну вектора швидкості за часом:
або
Формулу (2.15) називають формулою Ривальса, з якої випливає, що вектор прискорення точки
З урахуванням формул (2.11), (2.15) робимо висновок, що
Формули (2.16) є векторними виразами дотичного, нормального і повного прискорень точок твердого тіла, що обертається навколо нерухомої осі. Розташування цих векторів показано на рис. 2.7,а – при прискореному обертанні, рис. 2.7,б – при уповільненому обертанні).
Поиск по сайту: |
 . Тоді числове (алгебраїчне) значення швидкості точки відповідно до формули (1.19) буде
. Тоді числове (алгебраїчне) значення швидкості точки відповідно до формули (1.19) буде або
або  . (2.10)
. (2.10) спрямований по дотичній до описуваного точкою кола (або перпендикулярно площині П, що проходить через вісь обертання і точку М, або перпендикулярно прямої МР, що з'єднує точку М з віссю обертання) по напряму руху, що збігається з напрямом дугової стрілки кутової швидкості (рис. 2.2).
спрямований по дотичній до описуваного точкою кола (або перпендикулярно площині П, що проходить через вісь обертання і точку М, або перпендикулярно прямої МР, що з'єднує точку М з віссю обертання) по напряму руху, що збігається з напрямом дугової стрілки кутової швидкості (рис. 2.2). . Підставляючи до них значення V з рівності (2.10) і з урахуванням того, що в нашому випадку
. Підставляючи до них значення V з рівності (2.10) і з урахуванням того, що в нашому випадку  , одержимо:
, одержимо:  або остаточно:
або остаточно: . (2.11)
. (2.11) спрямована по дотичній до траєкторії точки у бік дугової стрілки кутового прискорення
спрямована по дотичній до траєкторії точки у бік дугової стрілки кутового прискорення  , нормальна складова
, нормальна складова  спрямована по радіусу МР до осі обертання (рис. 2.5).
спрямована по радіусу МР до осі обертання (рис. 2.5). ,
, або
або  . (2.12)
. (2.12)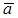 від радіуса описуваного точкою кола (від нормалі до траєкторії) визначається кутом
від радіуса описуваного точкою кола (від нормалі до траєкторії) визначається кутом  , що обчислюється за формулою (1.25)
, що обчислюється за формулою (1.25)  і, використовувавши рівняння (2.11), одержимо
і, використовувавши рівняння (2.11), одержимо . (2.13)
. (2.13) Рис. 2.4
Рис. 2.4
 Рис. 2.5
Рис. 2.5

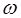 і
і  , оскільки вони є характеристиками руху всього тіла. Звідси випливає, що в даний момент часу кут
, оскільки вони є характеристиками руху всього тіла. Звідси випливає, що в даний момент часу кут  і
і  (рис. 2.7). З довільної точки Оосі обертання проведемо радіус-вектор
(рис. 2.7). З довільної точки Оосі обертання проведемо радіус-вектор  точки М (причому
точки М (причому  і
і  ).
).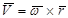 . (2.14)
. (2.14) збігається з раніше отриманим за формулою (2.10).
збігається з раніше отриманим за формулою (2.10).












 . (2.15)
. (2.15)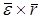 називають обертальною складовою прискорення. При обертанні тіла навколо нерухомої осі вектор
називають обертальною складовою прискорення. При обертанні тіла навколо нерухомої осі вектор  , а його модуль буде
, а його модуль буде  . Другий доданок у формулі (2.15) називають доосьовою складовою прискорення. При обертанні тіла навколо нерухомої осі вектор добутку
. Другий доданок у формулі (2.15) називають доосьовою складовою прискорення. При обертанні тіла навколо нерухомої осі вектор добутку  спрямований уздовж МР, тобто по головній нормалі до траєкторії точки М (позначимо його в цьому випадку
спрямований уздовж МР, тобто по головній нормалі до траєкторії точки М (позначимо його в цьому випадку  .
. . (2.16)
. (2.16)