 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Энергия затухающих колебаний ⇐ ПредыдущаяСтр 9 из 9
Примеры решения задач
Пример 1. Начальная фаза затухающих колебаний равна нулю. Период колебания N = 2 c, логарифмический декремент затухания χ = 0,5. Записать уравнение движения материальной точки при таких колебаниях, если через время t = 3Т смещение точки составляет 4 см.
Решение: Закон зависимости координаты точки х от времени t в общем виде 1. Т.к. логарифмический декремент затухания χ равен произведению коэффициента затухания δ на период Т
2. Циклическая частота
3. Начальная амплитуда А0 из уравнения в общем виде
Подставляя значения А0, δ, ω в закон колебания, получаем
Ответ:
Пример 2. Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась в 3 раза. Определить, во сколько раз она уменьшится за 4 мин.
Амплитуда последующих смещений маятника изменяется по экспоненте
аналогично
Из (1) найдем коэффициент затухания
Следовательно,
Ответ: за 4 мин амплитуда колебания маятника уменьшилась в 81 раз.
Пример 3. Определить добротность колебательного контура, состоящего из катушки индуктивностью L = 2 мГн, конденсатора емкостью С = 0,2 мкФ и резистора сопротивлением R = 1 Ом.
где χ – логарифмический декремент затухания.
где δ – коэффициент затухания; Т – период затухающих колебаний. Для колебательного контура
при малых затуханиях
Поэтому
Ответ: добротность контура равна Q = 100.
Список использованных источников
1. Трофимова, Т.И. Курс общей физики. – М.: Высш. шк., 2005 . – 541 с. 2. Трофимова, Т.И. Физика в таблицах и формулах. – М.: Дрофа, 2002. – 431 с. 3. Фриш, С.Э. , Тиморева, А.В. Курс общей физики. т.2 изд 9-е. – М.: Гос. изд-во ф-м. лит-ры, 1692 г. – 514 с. 4. Трофимова, Т.И. Сборник задач по физике. – М.: Высш. шк., 2001. – 590 с. 5. Чертов, А.Г., Воробьев, А.А. Задачник по физике. – М.: Высш. шк., 1988. – 527 с.
Матанцева Вера Анатольевна Ушакова Тамара Иосифовна Притыченко Лидия Митрофановна
ФИЗИКА Колебания и волны Методические указания для самостоятельной работы студентов БГИТА очной и заочной форм обучения
Лицензия НД № 14185 от 6.03.2001 г Формат 60×94 1/16. Тираж 50 экз. Печ. л. - 4,8 Брянская государственная инженерно-технологическая академия. 241037. г. Брянск, пр. Станке Димитрова, 3, редакционно-издательский отдел. Подразделение оперативной печати Подписано к печати
Поиск по сайту: |
 , имеем
, имеем
 ,
где Е0 – значение полной энергии колебательной системы в начальный момент времени.
Убыль энергии за один период колебания
,
где Е0 – значение полной энергии колебательной системы в начальный момент времени.
Убыль энергии за один период колебания
 Следовательно
Следовательно
 ,
т.е. при слабом затухании добротность Q с точностью до множителя
,
т.е. при слабом затухании добротность Q с точностью до множителя  , равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.
, равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.
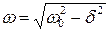 стремится к нулю, а период колебаний Т растет и при
стремится к нулю, а период колебаний Т растет и при  период
период 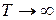 , т.е. движение перестает быть периодическим.
При
, т.е. движение перестает быть периодическим.
При  движение носит апериодический характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний
движение носит апериодический характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний

 равна собственной частоте ω0, при этом коэффициент затухания
равна собственной частоте ω0, при этом коэффициент затухания 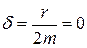 и колебания становятся незатухающими (идеальная механическая система)
и колебания становятся незатухающими (идеальная механическая система)
 и колебания в контуре становятся незатухающими (идеальный колебательный контур)
и колебания в контуре становятся незатухающими (идеальный колебательный контур)
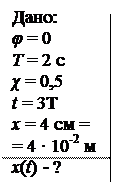
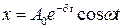 при φ = 0
при φ = 0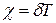 , то
, то 
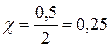 (с-1).
(с-1). ;
; 

 (м)
(м) (м)
(м) Решение:
Решение: , отсюда
, отсюда  (1)
(1) (2)
(2)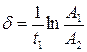 ;
;  (с-1)
(с-1)
 Добротность контура
Добротность контура ,
,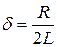 ;
; 
 .
.
