 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сложение взаимно перпендикулярных гармонических колебаний. Фигуры Лиссажу
Рассмотрим сложение взаимно перпендикулярных колебаний одинаковой частоты. Пусть начальная фаза первого колебания равна нулю φ01 = 0, а второго φ02 ≠ 0:
Найдем уравнение траектории колеблющейся материальной точки, т.е. функцию а) если разность фаз равна нулю
б) если разность фаз в) Если разность фаз Решая уравнения
получаем:
При разности фаз
Решая систему уравнений
получаем
Если амплитуды по х и y равны А = В, то точка движется по окружности. г) В общем случае произвольной разности фаз траектория также представляет собой эллипс, но с повернутыми осями и в зависимости от разности фаз наклон эллипса и направление движения точки разное (рисунок 3.4 в, г)
При сложении взаимно перпендикулярных гармонических колебаний не одинаковых частот, траектория результирующего движения имеет довольно сложный вид. Замкнутые траектории, описываемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Форма фигур Лиссажу зависит от отношения частот складываемых колебаний и разности фаз между ними (рисунок 3.5).
Примеры решения задач
Пример 1. Методом векторных диаграмм сложить два колебания одного направления:
Решение:
Представим законы смещения x1(t) и х2(t) соответственно данным задачи:
На оси ох из точки О построим вектор По правилу сложения векторов (правило параллелограмма) строим вектор Начальная фаза результирующего колебания из прямоугольного треугольника
Следовательно, результирующее колебание совершается по закону
Ответ:
Пример 2. Методом векторных диаграмм сложить два колебания одного направления:
Решение:
От точки О на оси ох отложены два вектора По формуле косинуса определяем модуль вектора результирующего колебания, построенного как векторная сумма
Начальную фазу колебания φ определяем из формулы
Так как частота результирующего колебания равна частотам слагаемых колебаний, то получаем следующий результат:
Ответ:
Решение:
Так как векторы
Начальная фаза результирующего колебания может быть найдена или по формуле
или по рисунку
Результирующее колебание совершается по закону
Ответ:
Пример 4. Точка участвует в двух взаимно перпендикулярных колебаниях, описываемых уравнениями
Решение:
Для определения направления движения зададим два условия: при t = 0 получим х = 0; y = 4; при
Поиск по сайту: |

 :
: , то
, то
 - уравнение прямой, т.е. траектория точки – отрезок прямой в I и III квадратах (рисунок 3.4 а);
- уравнение прямой, т.е. траектория точки – отрезок прямой в I и III квадратах (рисунок 3.4 а);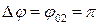 , то
, то  - аналогичная траектория, но расположенная во II и IV квадратах (рисунок 3.4 а – пунктирная прямая).
- аналогичная траектория, но расположенная во II и IV квадратах (рисунок 3.4 а – пунктирная прямая). , то
, то 

 - уравнение эллипса (рисунок 3.4 б) причем точка движется по часовой стрелке.
- уравнение эллипса (рисунок 3.4 б) причем точка движется по часовой стрелке.
 находим, что
находим, что



 и
и  . А1 = А2 = 3 см; ω1 = ω2 = π, τ = 0,5 с.
. А1 = А2 = 3 см; ω1 = ω2 = π, τ = 0,5 с.



 , равный амплитуде А1 = 3 ∙ 10-2 м при начальной фазе φ01 = 0. Из этой же точки О проведем вектор
, равный амплитуде А1 = 3 ∙ 10-2 м при начальной фазе φ01 = 0. Из этой же точки О проведем вектор  , по модулю равный амплитуде А2 под углом
, по модулю равный амплитуде А2 под углом 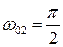 .
. . Модуль
. Модуль  (по теореме Пифагора).
(по теореме Пифагора). ;
;  ;
;


 и
и 

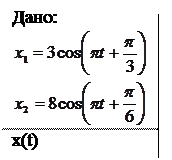
 , модули которых А = 3 м, А = 8 м под углами к оси ох, равными начальным фазам колебаний
, модули которых А = 3 м, А = 8 м под углами к оси ох, равными начальным фазам колебаний  и
и  .
.


 ;
;

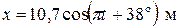 .
. Пример 3. Методом векторных диаграмм сложить два колебания одного направления:
Пример 3. Методом векторных диаграмм сложить два колебания одного направления:  и
и  .
. От точки О на оси ох отложим два вектора
От точки О на оси ох отложим два вектора  и
и  .
. , то по теореме Пифагора амплитуда результирующего колебания
, то по теореме Пифагора амплитуда результирующего колебания
 .
.
 ;
; 

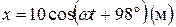 .
. .
.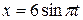 и
и  . Определить уравнение траектории и указать направление движения точки.
. Определить уравнение траектории и указать направление движения точки.
 Представим уравнения в виде:
Представим уравнения в виде:  ,
,  , возведя левые и правые части уравнений в квадрат и сложив их, получаем уравнение траектории:
, возведя левые и правые части уравнений в квадрат и сложив их, получаем уравнение траектории: - уравнение эллипса.
- уравнение эллипса. получаем х = 6; y = 0. Следовательно, движение точки по часовой стрелке.
получаем х = 6; y = 0. Следовательно, движение точки по часовой стрелке.