 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Момент инерции твердого тела относительно оси вращения
Момент инерции при вращательном движении имеет тот же смысл, что и масса при поступательном движении. Момент инерции – это мера инертности тела при вращательном движении. Момент инерции твердого тела зависит от размеров тела, его формы, от распределения плотности материала тела по его объему и от положения оси вращения. Любое твердое тело представляет собой совокупность материальных точек массой
Эта формула приближенная. Точной является формула
Пользуясь формулой (2.16), можно найти момент инерции для стержня длиной
для шара радиуса для диска радиуса
Если ось вращения
Здесь
Момент импульса материальной точки. Момент импульса твердого тела
Моментом импульса материальной точки массой m0 относительно произвольного центра вращения
где
Рис. 2.4 Так как твердое тело представляет собой совокупность материальных точек массой Dmi, то момент импульса твердого тела относительно произвольного центра вращения
где
] [
] [
Рис. 2.5
Момент импульса каждой материальной точки Dmi относительно оси Z определяется выражением
где Момент импульса твердого тела относительно оси Z равен векторной сумме моментов импульсов всех материальных точек:
Направлен вектор
Поиск по сайту: |
 , находящихся на расстоянии
, находящихся на расстоянии  от оси вращения. Момент инерции твердого тела относительно оси вращения:
от оси вращения. Момент инерции твердого тела относительно оси вращения: (2.15)
(2.15) . (2.16)
. (2.16) однородного тела правильной геометрической формы массой
однородного тела правильной геометрической формы массой  относительно оси, проходящей через центр масс тела
относительно оси, проходящей через центр масс тела  :
: (ось перпендикулярна стержню)
(ось перпендикулярна стержню) ; (2.17)
; (2.17)
 ; (2.18)
; (2.18) . (2.19)
. (2.19) не проходит через центр масс, то момент инерции относительно этой оси
не проходит через центр масс, то момент инерции относительно этой оси  определяется по теореме Штейнера:
определяется по теореме Штейнера: . (2.20)
. (2.20) - расстояние между осями.
- расстояние между осями. называется векторная величина, равная
называется векторная величина, равная , (2.21)
, (2.21)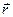 - радиус вращения, проведенный из центра
- радиус вращения, проведенный из центра  (рис. 2.4).
(рис. 2.4).


 , (2.21а)
, (2.21а) - радиус-вектор, проведенный от центра вращения
- радиус-вектор, проведенный от центра вращения  .
. В случае, когда ось вращения твердого тела закреплена и совпадает с осью Z, используется понятие – момент импульса твердого тела относительно оси вращения –
В случае, когда ось вращения твердого тела закреплена и совпадает с осью Z, используется понятие – момент импульса твердого тела относительно оси вращения –  (рис. 2.5). Z
(рис. 2.5). Z







 (2.22)
(2.22) , к началу вектора
, к началу вектора  . (2.23)
. (2.23)