 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Скорости волнового движения
Необходимо четко усвоить следующее: отдельные частицы, составляющие среду, не распространяются вместе с волнами через среду. Они гармонически колеблются в поперечном или продольном направлении относительно своих положений равновесия. Мы наблюдаем как волны их фазовые отношения, а не распространение частиц в среде. При волновом движении следует различать три скорости, которые представляют собой существенно различные величины.
Это выражение дает связь между временем Используя выражение (11) можно найти производную Продифференцируем выражение (11):
откуда
Таким образом, скорость распространения волны в среде
Такой волновой пакет или цуг волн можно представить как результат суперпозиции волн различной амплитуды и частоты. Если среда обладает дисперсией, т.е. скорость распространения является функцией частоты, такой волновой пакет будет "расплываться" в пространстве. Понятие "фазовая скорость" для пакета неприменимо. В этом случае удобно пользоваться понятием "групповая скорость". Это скорость перемещения огибающей в пространстве, или скорость переноса энергии.
Волновое уравнение.
Также, как уравнение гармонических колебании является решением дифференциального уравнения, называемого уравнением гармонического осциллятора, уравнение плоской волны является решением дифференциального уравнения второго порядка - волнового уравнения.
Но для малых колебаний можно считать, что
Перпендикулярно оси
Мы рассматриваем малые колебания, поэтому угол
Разность в квадратных скобках можно представить как произведение элемента расстояния
Таким образом, сила, действующая на элемент струны со стороны соседних элементов, выражается соотношением
Напишем второй закон Ньютона для этого элемента:
Отсюда
Отношение
Это соотношение называют волновым уравнением. Скорость распространения упругих волн на струне определяется ее линейной плотностью
Непосредственной подстановкой нетрудно убедиться, что уравнение плоской волны в форме (6) или (9), является решением волнового уравнения. Рассматривая движение малого объёма жидкости или газа при распространении в них упругих продольных волн, можно показать, что смещение выделенного элемента относительно положения равновесия также подчиняется волновому уравнению. Скорость звуковых волн в газах определяется следующим выражением
где
Стоячие волны.
В предыдущих параграфах мы рассматривали волны, распространяющиеся в безграничной среде. В ограниченном пространстве при возбуждении колебаний частиц среды возникает сложный волновой процесс за счет наложения первичной падающей волны и волн, отраженных от границ среды, а также от неоднородностей в самой среде. Рассмотрим простейший случай наложения двух плоских волн одинаковой амплитуды, распространяющихся навстречу друг другу. Возникающий в результате волновой процесс называют стоячей волной. Практически стоячие волны можно получить при отражении плоской волны от плоского препятствия. Плоская волна, распространяющаяся в положительном направлении оси
Плоская волна, распространяющаяся в отрицательном направлении уравнением
Складывая почленно оба уравнения и преобразовывая результат по формуле для суммы косинусов, получим
Используя определение волнового числа, формуле (23) можно придать следующий вид:
где Уравнение (24) является уравнением стоячей волны. Из него следует, что колебания любой частицы среды в стоячей волне совершаются с той же частотой, что и в исходных плоских волнах. Однако амплитуда колебаний различных частиц неодинакова, она зависит от координаты
амплитуда колебаний достигает максимального значения
В точках, где
амплитуда колебаний обращается в нуль. Эти точки называют узлами стоячей волны. Частицы среды, находящиеся в узловых точках, не совершают колебаний. Координаты узловых точек определяются соотношением
Из формул (26) и (28) следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно Выражение Первый график изображает распределение смещений в момент времени
Длинам волн
где
Поиск по сайту: |
 (10)
(10) (11)
(11) и местом (координатой)
и местом (координатой) 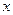 , в котором зафиксированное значение фазы реализуется в данный момент.
, в котором зафиксированное значение фазы реализуется в данный момент. , представляющую собой скорость, с которой перемещается в среде фиксированное значение фазы.
, представляющую собой скорость, с которой перемещается в среде фиксированное значение фазы.
 (12)
(12)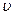 , которую мы ввели в соотношениях (4) и (5), есть серость перемещения фиксированного значения фазы, т.е. фазовая скорость.
, которую мы ввели в соотношениях (4) и (5), есть серость перемещения фиксированного значения фазы, т.е. фазовая скорость. Групповая скорость. Понятие "групповая скорость" является несколько более сложным, чем фазовая скорость. Оно будет подробнее рассматриваться в последующих курсах общей физики. Представление о групповой скорости возникает при изучении распространения волнового пакета или цуга волн в среде (рис. 3).
Групповая скорость. Понятие "групповая скорость" является несколько более сложным, чем фазовая скорость. Оно будет подробнее рассматриваться в последующих курсах общей физики. Представление о групповой скорости возникает при изучении распространения волнового пакета или цуга волн в среде (рис. 3).  Выведем волновое уравнение для частного случая распространения поперечных волн на бесконечной тонкой струне. Пусть ось
Выведем волновое уравнение для частного случая распространения поперечных волн на бесконечной тонкой струне. Пусть ось  обозначим смещение частиц струны при распространении по ней поперечной волны. Полагаем, что вдоль струны существует постоянное натяжение
обозначим смещение частиц струны при распространении по ней поперечной волны. Полагаем, что вдоль струны существует постоянное натяжение  . Масса однородной струны, приходящаяся на единицу длины, называется её линейной плотностью
. Масса однородной струны, приходящаяся на единицу длины, называется её линейной плотностью  . На искривленный элемент струны
. На искривленный элемент струны  (рис. 4) с одного конца действует натяжение
(рис. 4) с одного конца действует натяжение 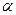 к оси
к оси  . Длинна искривленного участка
. Длинна искривленного участка 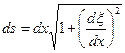 (13)
(13) мала и её квадратом можно пренебречь, и тогда
мала и её квадратом можно пренебречь, и тогда  . Следовательно, масса элемента струны равна
. Следовательно, масса элемента струны равна (14)
(14)
 . Тогда сила равна
. Тогда сила равна (15)
(15) на производную функции
на производную функции  (16)
(16) (17)
(17) (18)
(18) (19)
(19) имеет размерность квадрата скорости. Поэтому уравнение (19) можно переписать так:
имеет размерность квадрата скорости. Поэтому уравнение (19) можно переписать так: (20)
(20) (21)
(21) (22)
(22) и
и  отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
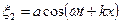
 (23)
(23) (24)
(24) - амплитуда колебаний, зависящая от координаты
- амплитуда колебаний, зависящая от координаты  в формуле (24). В точках, где
в формуле (24). В точках, где ,
,  (25)
(25) . Эти точки называют пучностями стоячей волны. Из соотношения (24) можно получить координаты пучностей:
. Эти точки называют пучностями стоячей волны. Из соотношения (24) можно получить координаты пучностей: ,
,  ,
,  ,
,  .
. в формуле (24) при переходе через нулевое значение меняет знак. Это означает, что фаза колебаний частиц среды разделённых узловой плоскостью, отличается на
в формуле (24) при переходе через нулевое значение меняет знак. Это означает, что фаза колебаний частиц среды разделённых узловой плоскостью, отличается на  . Все частицы среды, находящиеся между соседними узловыми совершают колебания в одинаковою фазе, но с различными амплитудами. Рисунок 5 поясняет эти выводы.
. Все частицы среды, находящиеся между соседними узловыми совершают колебания в одинаковою фазе, но с различными амплитудами. Рисунок 5 поясняет эти выводы. 
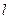 укладывается целое число полуволн:
укладывается целое число полуволн: или
или  ,
,  (29)
(29) соответствуют частоты
соответствуют частоты ,
,  называют собственными частотами колебаний струны. Аналогичная ситуация возникает при возбуждении стоячих звуковых волн в отрезке трубы, закрытом с торцов жёсткими крышками.
называют собственными частотами колебаний струны. Аналогичная ситуация возникает при возбуждении стоячих звуковых волн в отрезке трубы, закрытом с торцов жёсткими крышками.