 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рух частинки у центральному полі
Тема: Задача двох тіл та рух частинки у центрально-симетричному полі План:
Література: 1. Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика: Учеб. Пособие. –В 10-ти т. Т.1. Механика. – М.: Наука, 1988, §§11–15. 2. И.В. Савельев. Основы теоретической физики, т. 1. – М.: Наука, 1975, §§11–12. 3. А.М. Федорченко. Класична механіка і електродинаміка. – К.: Вища школа, 1992, §§11–12. 4. В.В. Мултановский. Курс теоретической физики: Классическая механика. Основы специальной теории относительности. Релятивистская механика: учебное пособие для студентов физ.-мат. фак. пед. ин-тов. – М.: Просвещение, 1988, §27 5. Н.И. Жирнов Классическая механика: Учеб. Пособие для студентов физ.-мат. фак. пед. ин-тов. – М.: Просвещение, 1980, §§13,14,17–19
Задача двох тіл Задача про рух двох частинок, що взаємодіють між собою, зводиться до задачі одного тіла і розв’язується повністю. Вона може бути зведена до двох задач (одночастинних): задачі про рух центру мас; рух точки зведеної маси відносно центру мас. Нехай, ми маємо систему з двох частинок масами
Між ними діють сили взаємодії, а зовнішні сили відсутні. Тоді, рівняння, що описують рух цих частинок окремо матимуть вигляд:
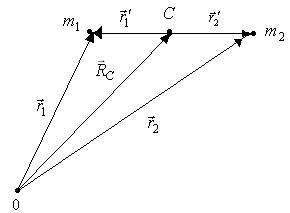
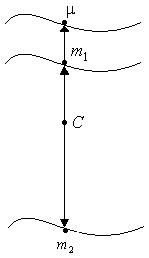
Оберемо нову систему відліку – систему із початком у центрі мас цих двох частинок.
Ця система рухається із постійною швидкістю. Коли центр (початок координат) нової системи співпадає із точкою
Значить, якщо знайти Введемо ще одну величину – відносну координату: тоді, помножуючи праву і ліву частину цього рівняння на
Враховуючи рівняння (3) матимемо:
і підставимо в (4):
тоді матимемо, що:
Тоді для швидкостей:
А рівняння руху (1) набудуть вигляду:
Позначимо за Тоді Аналогічно:
Отже, рух двох точок розглядається як рух однієї із зведеною масою Із координатою
Таким чином, траєкторії руху заданих точок Отже таким чином задача розв’язана.
Рух частинки у центральному полі Як відомо, центрально-симетричне поле – це поле, в якому потенціальна енергія є функцією лише від віддалі від нерухомого центра до рухомої матеріальної точки, т. т.
Коли ми маємо дві матеріальні точки, то як ми вже бачили у попередньому питанні, їх рух може бути описаний в Ц-системі (системі пов’язаної із центром мас системи) як рух точки зведеної маси, т.т. зводиться до руху однієї точки.. Як відомо, момент імпульсу матеріальної точки
Тоді у цій системі відліку момент імпульсу матеріальної точки має вигляд:
Отже, Повна енергія такої матеріальної точки:
А тепер намітимо шлях розв’язання основної задачі механіки. Використовуючи отримані нами інтеграли руху (1) і (2) можна відшукати рівняння траєкторії матеріальної точки, а саме:
Оскільки
де Таким чином, можна ввести поняття ефективної потенціальної енергії:
Ефективний потенціал (4) складається з двох доданків, кожний з яких є функціями лише координати
Обчислити інтеграл (а це можна зробити врахувавши відповідні граничні умови) можна відшукати і Після цього:
Можна одержати рівняння руху і в загальному вигляді:
Це і є рівняння траєкторії Відзначимо особливості одержаних результатів. p З формули (6) випливає, що p
Ці точки називають точками повороту, в них змінюється Область допустимих значень
Коли ця умова виконується тоді Закони Кеплера. Одна з найцікавіших і найважливіших задач – є задача про рух в полі сил тяжіння. Задачу про рух двох частинок, які взаємодіють за законом:
Оскільки це поле є центрально-симетричним, тоді для нього годяться всі висновки, які ми отримали вище. Але ми для розв’язання задачі Кеплера скористаємось дещо іншим прийомом для відшукання траєкторії руху частинки в так-званому кулонівському полі. Відшукаємо лагранжіан точки зведеної маси:
Кінетична енергія точки:
Потенціальна енергія точки:
Для центрально-симетричного поля:
Враховуючи також формулу (1), матимемо:
Нехай
Як відомо Значить:
А тому, використовуючи перше рівняння Лагранжа, матимемо:
Окрім того:
Тоді із урахуванням рівняння (5) – (6) матиме зміст подвійної секторної швидкості:
Тепер складемо друге рівняння Лагранжа:
Враховуючи (3), матимемо:
Далі:
отже:
Тоді:
Ця величина Скористаємось інтегралом площини (7), тоді одержимо, що інтеграл площини
і рівняння (8) матиме вигляд:
Для інтегрування цього рівняння виконаємо заміну Для цього використаємо інтеграл площини (10), тобто:
Тоді рівняння (11) матиме вигляд:
Щоб спростити це диференціальне рівняння виконаємо заміну, нехай:
Тоді
отже:
значить,
Враховуючи (13):
Це диференціальне рівняння другого порядку з постійними коефіцієнтами і розв’язується згідно загальних правил:
1) 2) Його характеристичне рівняння матиме вигляд:
Тобто загальний розв’язок цього однорідного рівняння:
або
де
Таким чином, загальний інтеграл (15) дає рівняння кривої другого порядку у полярних координатах:
Ми бачимо, що рух тіла маси
Як відомо, характер кривої другого порядку визначається величинами Як ми вже бачили, інтеграл енергії має в цьому випадку вигляд:
А кінетична енергія радіального руху:
Побудуємо графік залежності ефективного потенціалу від відстані до силового центру
Умова 1. 2. 3. 4. Таким чином, розв’язуючи задачу Кеплера ми можемо також дуже легко встановити закони Кеплера: Перший закон Кеплера: Всі планети рухаються навколо Сонця по еліпсах, в одному з фокусів якого знаходиться Сонце. Цей закон ми одержали, розв’язуючи Кеплерову задачу. Уточнімо: в одному з фокусів еліпса знаходиться не Сонце, а центр має системи „Сонце-планета”. Другий закон Кеплера:.радіус-вектор планети за рівні проміжки часу описують рівні площі. Цей закон ми одержали у вигляді інтеграла площини: Інакше: секторна швидкість руху планети є величиною сталою. Третій закон Кеплера: Ми бачили, що:
Крім того:
Тому, що
Значить:
Але
тут Коли врахувати рух зведеної маси
Частинка з більшою масою описуватиме менший еліпс, меншої – більший, зведена маса
Таким чином: Тому:
де Значить, Квадрати періодів планет відносяться до кубів півосей для всіх планет майже однаково (адже Розглянуту тут теорію можна було б застосувати і до атома водню. Однак у цьому разі теорія не узгоджується з експериментом, бо класична механіка тут не застосовна, і атом водню треба описувати за допомогою квантової механіки. Безумовно, всі три закони Кеплера справедливі для руху як природних так і штучних супутників планет. Варто, одна пам’ятати, що ці закони виконуються лише в тих умовах, в яких вони одержані. Зокрема ми припустили, що на кожну планету діє гравітаційна сила тільки з боку Сонця і що взаємодія між планетами незначна. Завдяки великій масі Сонця, рух планет визначається в основному Сонцем, проте взаємодією між планетами не завжди можна знехтувати. Повчальною є історія відкриття планети Нептун. Було помічено, що траєкторія планети Уран (на той час остання з відомих планет Сонячної системи) в певний момент часу помітно відхилялася від еліпса. У. Лавер’є припустив, що це відхилення пожна пояснити дією на планету Уран іншої, ще невідомої планети. Виходячи з цього припущення, Лавер’є підрахував, якою мають бути її маса і траєкторія, щоб відхилення орбіти від точного еліпса збіглося з цими спостереженнями. Знаючи траєкторію, Лавер’є зміг також визначити координати цієї планети в будь-який момент часу. Справді, 23 вересня 1846 р. Й. Галле знайшов у визначеному місці цю планету, яку потім назвав Нептуном. Так, „на кінчику пера” було відкрито нову планету. Це була перемога людського розуму, який спирався на знання законів природи. Космічні швидкості. Висновки з попередніх питань повністю можна поширити і на рух штучних супутників Землі та космічних кораблів. При цьому нехтуватимемо опором повітря і, якщо тіла рухаються біля поверхні Землі, не враховуватимемо сил гравітаційного тяжіння Сонця, Місяця та планет. Повна енергія супутника або космічного корабля у полі земного тяжіння:
де Як вже зазначалося рух буде обмеженим, тобто відбуватиметься по еліптичні траєкторії, якщо
Звідси дістанемо, що
Взявши, що Швидкість, яку повинен мати супутник, щоб рухатися по коловій орбіті навколо Землі, називають першою космічною швидкістю. Рух супутника відбуватиметься по параболі, тобто буде необмеженим, за умови, що
Швидкість Відшукаємо мінімальне і максимальне значення третьої космічної швидкості корабля. Точне визначення третьої космічної швидкості має ряд значних утруднень, оскільки слід враховувати гравітаційні взаємодії трьох тіл: Сонця, Землі і космічного корабля. Однак таке обчислення значно спрощується, якщо нехтувати дією поля сонячного тяжіння на рух космічного корабля протягом всього часу, який потрібний для виходу його поза зону дії земного тяжіння. Це пояснюється тим, що дія поля сонячного тяжіння повністю компенсується силами інерції, які виникають внаслідок руху Землі навколо Сонця. Позначимо швидкості корабля відносно Землі
де
Враховуючи, те, що
Нехтуючи дією поля сонячного тяжіння, закон збереження імпульсу цих станів можна записати у такій формі:
Звідси маємо
Підставивши вираз
Підставляючи числові значення у (6), дістанемо Якщо космічний корабель посилають у протилежному напрямі до напряму руху Землі, тоді третя космічна швидкість максимальна. Виконуючи аналогічні розрахунки, враховуючи зміну напрямку можна одержати, що
Н.В. Подопригора
Поиск по сайту: |
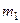 і
і 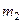 .
.
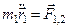
 (1)
(1) (2)
(2) , то
, то  , тоді
, тоді  і
і 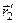 – радіус-вектори
– радіус-вектори 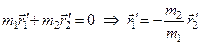 . (3)
. (3)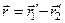 ,
, (4)
(4)
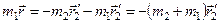 ,
,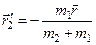 ;
; .
.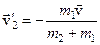 ;
;  (5)
(5)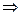
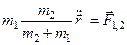
 й назвемо цю величину зведеною масою
й назвемо цю величину зведеною масою .
.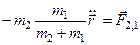 , або
, або  , тобто
, тобто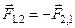 .
. Коли вигляд силового поля
Коли вигляд силового поля  відомий, то можна відшукати й
відомий, то можна відшукати й 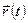 , а потім:
, а потім: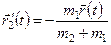 ,
,  . а також
. а також ,
, 
 є подібні криві, відносно центру мас системи, причому
є подібні криві, відносно центру мас системи, причому  . Відповідно можна відшукати й швидкості точок з рівнянь (5).
. Відповідно можна відшукати й швидкості точок з рівнянь (5).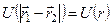
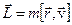 у центрально-симетричному полі є інтегралом руху, тобто зберігається за модулем і за напрямком, а якщо так
у центрально-симетричному полі є інтегралом руху, тобто зберігається за модулем і за напрямком, а якщо так  і
і  – лежать в одній площині перпендикулярній до
– лежать в одній площині перпендикулярній до  , що не змінює свого положення в просторі або іншими словами: рух – плоский. Траєкторія такого руху – плоска крива, а ому така тачка має лише дві ступені вільності.
, що не змінює свого положення в просторі або іншими словами: рух – плоский. Траєкторія такого руху – плоска крива, а ому така тачка має лише дві ступені вільності. Тому для опису руху точки у центрально-симетричному полі зручно використати полярну систему координат: полюс (сумістити із центром мас системи –
Тому для опису руху точки у центрально-симетричному полі зручно використати полярну систему координат: полюс (сумістити із центром мас системи – 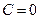 ), радіус вектор (його довжина (
), радіус вектор (його довжина (  ), азимут –
), азимут – 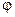 . Тобто площина
. Тобто площина  співпадає з полярною системою координат
співпадає з полярною системою координат 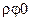 ;
;  .
.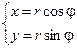



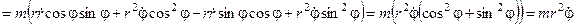
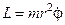 (1)
(1)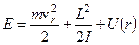 , або
, або  ;
; (2)
(2) і
і 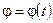
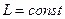 , тому
, тому  ;
; 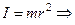
 , значить
, значить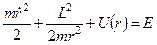 , (3)
, (3) – відцентрова потенціальна енергія.
– відцентрова потенціальна енергія. (4)
(4)
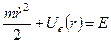 допускає розділення змінних:
допускає розділення змінних: ;
;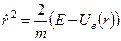
 ;
;
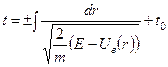 (5)
(5) .
.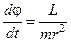 ;
;  ;
;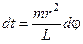 ;
;
 (6)
(6) .
.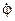 не змінюється, а тому
не змінюється, а тому  – змінюється монотонно.
– змінюється монотонно.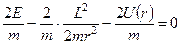
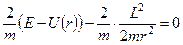 ;
;
 , а
, а 
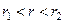 , причому
, причому 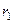 і
і 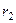 відмінні від
відмінні від  і
і  й рух частинки вважається фінітний, коли
й рух частинки вважається фінітний, коли 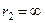 , то рух – інфінітний.
, то рух – інфінітний. (1)
(1) ; (2)
; (2) ;
; ;
; ;
; 
 :
: ; (3)
; (3) ;
;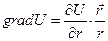 ;
;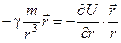 ;
;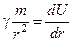 ;
;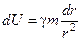 ;
;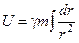 ;
; . (4)
. (4)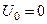 і із урахуванням (3) і (4) рівняння (2) матиме вигляд:
і із урахуванням (3) і (4) рівняння (2) матиме вигляд: (5)
(5)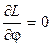 і
і  (6)
(6) .
.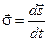 – секторна швидкість матеріальної точки, де:
– секторна швидкість матеріальної точки, де: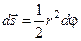 ,
, 
 . (7)
. (7)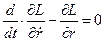 ;
; ;
; 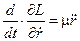 .
. ,
, ;
;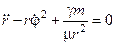 . (8),
. (8), . (9)
. (9) за звичай близька до одиниці, бо
за звичай близька до одиниці, бо  .
. (10)
(10) ;
; . (11)
. (11)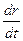 через
через 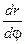 .
.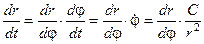 ;
; .
. .
. (12)
(12) ,
,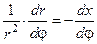 (13)
(13) , тоді:
, тоді:
 ;
;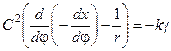 ;
; ;
; (14)
(14)
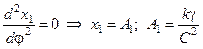 .
.
 ;
; , тобто матимуть уявні значення, тому:
, тобто матимуть уявні значення, тому: ,
,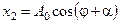 ,
,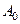 і
і  – довільні сталі. Отже остаточно:
– довільні сталі. Отже остаточно: або
або  ;
; (15)
(15)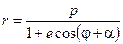 , де
, де  ,
, – параметр кривої,
– параметр кривої, 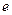 – ексцентриситет кривої.
– ексцентриситет кривої. в полі сили тяжіння тіла маси
в полі сили тяжіння тіла маси 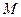 приводить до траєкторії кривої другого порядку, де:
приводить до траєкторії кривої другого порядку, де: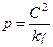 – параметр цієї кривої, а
– параметр цієї кривої, а – ексцентриситет цієї кривої, причому
– ексцентриситет цієї кривої, причому , де
, де  – гравітаційна стала;
– гравітаційна стала; ;
; , де
, де  – ефективний потенціал;
– ефективний потенціал; .
.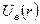 і проведемо прямі
і проведемо прямі  для різних значень повної енергії.
для різних значень повної енергії.
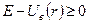 виконується для наступних рухів:
виконується для наступних рухів: , тоді
, тоді  . Такий рух буде інфінітний і відповідає гіперболічній траєкторії.
. Такий рух буде інфінітний і відповідає гіперболічній траєкторії. , тоді
, тоді  . Рух також інфінітний і відбувається за параболічною траєкторією.
. Рух також інфінітний і відбувається за параболічною траєкторією. , тоді
, тоді  . Рух фінітний і за еліптичною траєкторією.
. Рух фінітний і за еліптичною траєкторією. , тоді
, тоді 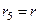 . Рух фінітний і по колу.
. Рух фінітний і по колу.
 ;
; ;
; ;
; 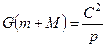 .
. , де
, де 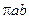 – площа еліпса,
– площа еліпса, 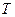 – період обертання планети,
– період обертання планети,  – велика,
– велика, 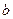 – і мала півосі еліпса.
– і мала півосі еліпса. .
. , тому
, тому ,
,
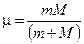 – має ще меншу масу, порівняймо:
– має ще меншу масу, порівняймо: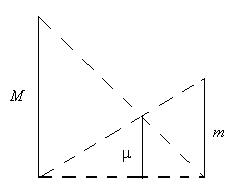
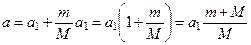 .
.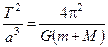 , (16)
, (16) За умови, що
За умови, що 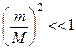 і
і  .
.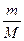 – величина мала).
– величина мала). , (1)
, (1) . Окремим випадком такого руху буде рух по коловій траєкторії. При цьому сила тяжіння відіграє роль доцентрової сили, тобто:
. Окремим випадком такого руху буде рух по коловій траєкторії. При цьому сила тяжіння відіграє роль доцентрової сили, тобто: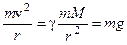

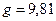 м/с2,
м/с2,  м, дістанемо, що
м, дістанемо, що  м/с
м/с  км/с.
км/с. . Тоді швидкість руху з урахуванням (1):
. Тоді швидкість руху з урахуванням (1): ;
;  км/с
км/с називають другою космічною швидкістю. Це та найменша швидкість, яку потрібно надати тілу, щоб воно ніколи не повернулося на Землю. Можна надати тілу і таку швидкість, щоб воно залишило Сонячну систему. Цю швидкість називають третьою космічною швидкістю.
називають другою космічною швидкістю. Це та найменша швидкість, яку потрібно надати тілу, щоб воно ніколи не повернулося на Землю. Можна надати тілу і таку швидкість, щоб воно залишило Сонячну систему. Цю швидкість називають третьою космічною швидкістю.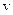 ,
,  ,
,  ,
,  ,
,  . Якщо корабель виходить із зони дії земного тяжіння з параболічною швидкістю відносно Сонця, то відносно Землі ця швидкість буде третьою космічною швидкістю, яку позначимо через
. Якщо корабель виходить із зони дії земного тяжіння з параболічною швидкістю відносно Сонця, то відносно Землі ця швидкість буде третьою космічною швидкістю, яку позначимо через 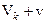 , а після виходу із зони земного тяжіння ця швидкість стане параболічною, тобто
, а після виходу із зони земного тяжіння ця швидкість стане параболічною, тобто  (2)
(2) , то рівняння (2) запишемо так:
, то рівняння (2) запишемо так: . (3)
. (3) і
і  , рівняння (3) можна записати як
, рівняння (3) можна записати як

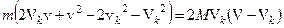 (4)
(4)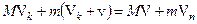 (5)
(5)
 у рівняння (4), знаходимо мінімальне значення третьої космічної швидкості:
у рівняння (4), знаходимо мінімальне значення третьої космічної швидкості: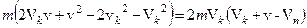



 , оскільки
, оскільки 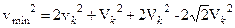

 (6)
(6) км/с.
км/с.