 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кинетический момент точки и системы относительно центра и оси
Билет 14 Вопрос 1 Под физическим маятником можно понимать любое тело, совершающее малые колебания относительно неподвижной горизонтальной оси под действием силы тяжести.
Как опытным путем определить положение центра тяжести тела сложной формы относительно оси (расстояние ОС ), рассматривалось в разделе “Статика”. По измеренному периоду колебаний этого тела можно определить его момент инерции относительно оси Oz, проходящей через точку О, и относительно горизонтальной оси, проходящей через центр масс тела. Интересно знать ещё и следующее. У колеблющихся физических тел на продолжении линии, проходящей через ось вращения и центр тяжести тела, существует точка, которую называют центром качаний. Если тело заставить колебаться относительно оси, проходящей через центр качаний, то период колебаний этого тела будет точно таким же, как и при колебаниях относительно оси, проходящей через точку О. Находится центр качаний (т. D на рисунке) на продолжении линии ОС ниже центра тяжести тела на расстоянии, которое принято называть приведенной длиной физического маятника. Дадим этому понятию следующее определение. Под приведенной длиной физического маятника понимается длина математического Маятника, период колебаний которого равен периоду колебаний физического маятника. Приведенную длину маятника легко определить, приравняв выражения, из которых определяются циклическая частота колебаний в каждом из случаев.
Вопрос 2 Кинетический момент точки и системы относительно центра и оси Рассмотрим систему материальных точек с массами m1m2....mn, имеющих в данный момент скорости v1v2.....vnотносительно инерциальной системы отсчета. Выберем произвольный центр О (Рис.1). Кинетическим моментом точки mjотносительно центра О называется вектор момента ее количества движения относительно этого центра.
Koj=mo(qj)=rjmjvj (j=1,2...n) (1) Известно, что векторное умножение можно записать через присоединенную матрицу первого сомножителя- радиуса вектора r. Опуская индекс j, запишем матричное выражение в осях xyz c началом в О: Ko=mRv (2) где R- кососимметричная присоединенная матрица столбца r
Проекция кинетического момента на ось называются кинетическим моментом точки относительно оси. Он вычисляется либо аналитически по формулам (3), либо как момент силы относительно оси. Момент дает только касательная составляющая вектора q (Рис.2). KZ= +qth (4) Момент обращается в ноль, если вектор количества движения (скорость точки) лежит в одной плоскости с осью (параллелен или пересекает ось) Кинетическим моментом системыотносительно центра О называется главный момент количеств движений точек системы относительно этого центра. Ko=SKoj=Smjrjvj (5) Аналогично с формулой (3) проекции вектора (4) образуют столбец кинетических моментов относительно осей координат Кинетическим моментом механической системы относительно полюса (оси) называют векторную (алгебраическую) сумму моментов количеств движения всех точек системы относительно этого же полюса О (той же оси)
Кинетический момент механической системы часто называют главным моментом количества движения системы соответственно относительно полюса или оси. Если спроектировать кинетический момент
Если система материальных точек движется поступательно, то Мы воспользовались свойством сочетательности векторного произведения относительно скалярного множителя и формулой для определения радиуса - вектора центра масс (2.4). Таким образом, кинетический момент системы относительно полюса при поступательном движении равен моменту количества движения системы относительно этого полюса, при условии, что количество движения системы приложено в центре масс. ^ Кинетический момент твердого тела относительно оси вращения
Пусть твердое тело вращается вокруг неподвижной оси
причём количество движения точки
Для всего тела то есть Кинетический момент вращающегося тела относительно оси вращения равен произведению угловой скорости тела на его момент инерции относительно оси вращения. Билет 15 Вопрос 1 Согласно принципу возможных перемещений (основному уравнению статики), для того, чтобы механическая система, на которую наложены идеальные, стационарные, удерживающие и голономные связи, находилась в равновесии, необходимо и достаточно, чтобы в этой системе были равны нулю все обобщенные силы:
где Qj - обобщенная сила, соответствующая j - ой обобщенной координате; s - число обобщенных координат в механической системе. Если для исследуемой системы были составлены дифференциальные уравнения движения в форме уравнений Лагранжа II - го рода, то для определения возможных положений равновесия достаточно приравнять обобщенные силы нулю и решить полученные уравнения относительно обобщенных координат. Если механическая система находится в равновесии в потенциальном силовом поле, то из уравнений (1) получаем следующие условия равновесия:
Следовательно, в положении равновесия потенциальная энергия имеет экстремальное значение. Не всякое равновесие, определяемое вышеприведенными формулами, может быть реализовано практически. В зависимости от поведения системы при отклонении от положения равновесия говорят об устойчивости или неустойчивости данного положения. Равновесие механической системы, состояние механической системы, находящейся под действием сил, при котором все её точки покоятся по отношению к рассматриваемой системе отсчёта. Если система отсчёта является инерциальной (см. Инерциальная система отсчёта),равновесие называется абсолютным, в противном случае — относительным. Изучение условий Р. м. с. — одна из основных задач статики. Условия Р. м. с. имеют вид равенств, связывающих действующие силы и параметры, определяющие положение системы; число этих условий равно числу степеней свободы системы. Условия относительности Р. м. с. составляются так же, как и условия абсолютного равновесия, если к действующим на точки силам прибавить соответствующие переносные силы инерции. Условия равновесия свободного твёрдого тела состоят в равенстве нулю сумм проекций на три координатные оси Oxyz и сумм моментов относительно этих осей всех приложенных к телу сил, т. е. При выполнении условий (1) тело будет по отношению к данной системе отсчёта находиться в покое, если скорости всех его точек относительно этой системы в момент начала действия сил были равны нулю. В противном случае тело при выполнении условий (1) будет совершать т. н. движение по инерции, например двигаться поступательно, равномерно и прямолинейно. Если твёрдое тело не является свободным (см. Связи механические), то условия его равновесия дают те из равенств (1) (или их следствий), которые не содержат реакций наложенных связей; остальные равенства дают уравнения для определения неизвестных реакций. Например, для тела, имеющего неподвижную ось вращения Oz, условием равновесия будет åmz(Fk) = 0; остальные равенства (1) служат для определения реакций подшипников, закрепляющих ось. Если тело закреплено наложенными связями жестко, то все равенства (1) дают уравнения для определённой реакции связей. Такого рода задачи часто решаются в технике. На основании отвердевания принципа равенства (1), не содержащие реакций внешних связей, дают одновременно необходимые (но недостаточные) условия равновесия любой механической системы и, в частности, деформируемого тела. Необходимые и достаточные условия равновесия любой механической системы могут быть найдены с помощью возможных перемещений принципа. Для системы, имеющей s степеней свободы, эти условия состоят в равенстве нулю соответствующих обобщённых сил: Q1= 0, Q2= 0, ×××, Qs= 0. (2) Из состояний равновесия, определяемых условиями (1) и (2), практически реализуются лишь те, которые являются устойчивыми (см. Устойчивость равновесия). Равновесия жидкостей и газов рассматриваются в гидростатике и аэростатике. Вопрос 2
Билет 18 Вопрос 1 для уравновешенной системы сил уже в соответствии с принципом возможных перемещений сумма виртуальных работ сил на любом возможном перемещении системы должна быть равна нулю.
Сформулировать записанное можно следующим образом. В любой момент движения механической системы с идеальными связями сумма виртуальных работ активных сил и сил инерции на любом возможном перемещении системы равна нулю. Это равенство принято называть общим уравнением динамики или принципом Лагранжа-Даламбера. Вопрос 2
“принцип возможных перемещений”.
Этот принцип считается наиболее общим условием равновесия или равномерного движения любой механической системы. Из него можно получить все аналитические условия равновесия тела под действием системы сил, рассматриваемые в разделе “Статика”.
Формулируется принцип следующим образом: Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ активных сил на любом возможном перемещении системы была равна нулю.
Для доказательства необходимости этого условия равновесия любой находящейся в покое механической системы, разделим силы, действующие на любую точку системы, на заданные и силы реакции связей.
Билет 19 Вопрос 1 Приближенная теория гироскопа Гироскопом называют тело, имеющее неподвижную точку и вращающееся вокруг оси материальной симметрии. Предположим, что гироскоп вращается с угловой скоростью вокруг собственной оси симметрии. В этом случае кинетический момент
Это одна из важнейших характеристик при движении гироскопа.
В приближенной теории гироскопа принимают, что 1 << и кинетический момент гироскопа равен
Гироскоп с тремя степенями свободы Гироскоп с тремя степенями свободы способен сопротивляться попытке изменения оси вращения гироскопа. Рассмотрим гироскоп, у которого неподвижная точка совпадает с центром масс. Рассмотрим сначала покоящийся гироскоп ( = 0, L = 0). Если к гироскопу приложить силу Рассмотрим вращающийся (быстро) гироскоп. Прикладываем силу По теореме об изменении кинетического момента
Момент перпендикулярен к плоскости чертежа, тогда
Если к оси гироскопа прикладывается сила, то ось гироскопа смещается перпендикулярно действующей силе по направлению вращающего момента. Если действие силы прекращается, то ось вращения гироскопа останавливается. ^ Говорят, что гироскоп способен противодействовать действию внешних сил. Рассмотрим случай регулярной прецессии. Имеется гироскоп, у которого центр масс не совпадает с неподвижной точкой. На тело действует сила Допустим OC = h, тогда
Отметим: Под действием силы тяжести ось гироскопа будет вращаться вокруг вертикальной оси z. Такое явление называется регулярной прецессией. Введем угловую скорость 1 – это угловая скорость, с которой ось гироскопа вращается вокруг оси z, ее еще называют “угловая скорость прецессии”.
Движение юлы – очень хороший пример движения гироскопа. Гироскоп с тремя степенями свободы находит широкое применение в современных системах ориентирования (гирокомпас, гирогоризонт …). Вопрос 2 ОБОБЩЁННЫЕ КООРДИНАТЫ независимые параметры qi (i=1, 2, ..., s) любой размерности, число к-рых равно числу s степеней свободы механич. системы и к-рые однозначно определяют положение системы. Закон движения системы в О. к. даётся s ур-ниями вида qi=qi(t), где t — время. О. к. пользуются при решении мн. задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число ур-ний, описывающих движение системы, по сравнению, напр., с ур-ниями в декартовых координатах (см. ЛАГРАНЖА УРАВНЕНИЯ В МЕХАНИКЕ). В системах с бесконечно большим числом степеней свободы (сплошные среды, физ. поля) О. к. являются особые функции пространственных координат и времени, наз. потенциалами, волн. функциями и т. п. В механике, степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая положение системы или тела (а вместе с их производными по времени — соответствующими скоростями - полностью определяющая состояние механической системы или тела - то есть их положение и движение). Число степеней свободы- это количество независимых перемещений, при котором состояние системы меняется!
Таким образом, обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная коэффициенту при вариации данной обобщенной координаты в выражении возможной работы сил, действующих на механическую систему. В общем случае обобщенная сила является функцией обобщенных координат, скоростей точек системы и времени. Из определения следует, что обобщенная сила — скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы. Так, для диска радиусом r и массой m, который катится без скольжения по наклонной плоскости (рис. 18.8), за обобщенные координаты можно принять либо s — координата центра масс диска, либо "фи" — угол поворота диска. .4.1. Обобщенная сила системы с одной степенью свободы
Для системы с одной степенью свободы обобщенной силой, соответствующей обобщенной координате q, называют величину, определяемую формулой
где q – малое приращение обобщенной координаты; Билет 21 Вопрос 1 Уравнения двухстепенного гироскопа. Уравнения двухстепенного гироскопа получаются автоматически из полученных ранее уравнений трехстепенного гироскопа.
Если
Гироскопический момент:
θ - угол нутации ω1 - угловая скорость собственного вращения ω2 - скорость прецессии Jz - момент инерции
Нутация — слабое нерегулярное движение вращающегося твёрдого тела, совершающего прецессию. Прецессия — явление, при котором ось вращающегося объекта поворачивается, например, под действием внешних моментов. Наблюдать прецессию достаточно просто. Достаточно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Правило Жуковского: Если гироскопу сообщают вынужденное прецессионное движение, то возникает гироскопическая пара сил, стремящаяся сделать ось гироскопа параллельной оси симметрии, причем так, чтобы направления вращения стали одинаковыми после их совпадения. Вопрос 2 Если голономная механическая система описывается лагранжианом
где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы. Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид
где По сравнению с ур-ниями в декартовых координатах (см., напр., ур-ния Лагранжа 1-го рода) ур-ния (3) обладают тем важным преимуществом, что число их равно числу степеней свободы системы и не зависит от кол-ва входящих в систему материальных частиц или тел; кроме того, при идеальных связях из ур-ний (3) автоматически исключаются все наперёд неизвестные реакции связей. Л. у. 2-го рода, дающими весьма общий и притом достаточно простой метод решения задач, широко пользуются для изучения движения разл. механич. систем, в частности в динамике механизмов и машин, в теории гироскопа ,в теории колебаний и др. Билет 22 Вопрос 1
Поиск по сайту: |



 =m
=m 
 =m
=m  (3)
(3)
 (6)
(6) (
(  ) . (3.22)
) . (3.22) из (3.22) на прямоугольные декартовы оси координат, то получим проекции кинетического момента на эти оси или кинетические моменты относительно осей координат
из (3.22) на прямоугольные декартовы оси координат, то получим проекции кинетического момента на эти оси или кинетические моменты относительно осей координат и, следовательно,
и, следовательно,  .
.
 с угловой скоростью
с угловой скоростью  (рис. 18). Выберем произвольную точку
(рис. 18). Выберем произвольную точку  в твердом теле и вычислим кинетический момент этого тела относительно оси вращения. По определению кинетического момента системы относительно оси имеем
в твердом теле и вычислим кинетический момент этого тела относительно оси вращения. По определению кинетического момента системы относительно оси имеем .
. ,
, -
-  перпендикулярно отрезку
перпендикулярно отрезку  и находится в плоскости, перпендикулярной оси вращения
и находится в плоскости, перпендикулярной оси вращения  . Следовательно, момент количества движения относительно оси
. Следовательно, момент количества движения относительно оси  для точки
для точки 
 .
. ,
, . (3.24)
. (3.24) (1)
(1) (2)
(2)








 , то очевидно, что гироскоп получит вращательное движение и упадет (т.е. ось гироскопа будет поворачиваться в плоскости чертежа).
, то очевидно, что гироскоп получит вращательное движение и упадет (т.е. ось гироскопа будет поворачиваться в плоскости чертежа).





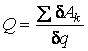 , (1.3)
, (1.3) – сумма элементарных работ сил системы на ее возможном перемещении.
– сумма элементарных работ сил системы на ее возможном перемещении.

 определяет движение двухстепенного гироскопа. Второе уравнение описывает движение корпуса, на котором установлен двухстепенной гироскоп.
определяет движение двухстепенного гироскопа. Второе уравнение описывает движение корпуса, на котором установлен двухстепенной гироскоп.
 (момент инерции) тела велик, а гироскопический момент
(момент инерции) тела велик, а гироскопический момент  мал, то уравнение (2) может вообще не учитываться и пользоваться только (1).
мал, то уравнение (2) может вообще не учитываться и пользоваться только (1).




 (
(  — обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид
— обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид

 — кинетическая энергия системы,
— кинетическая энергия системы,  — обобщённая сила.
— обобщённая сила.