 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рассмотрение данного вопроса начнём с простых примеров
Пример 2.11. Вычислить интеграл Решение. т.е. значение данного интеграла равно 1. Исходя из геометрического смысла определённого интеграла, мы вычислили площадь фигуры, изображённой на рисунке 2.19
Рис. 2.19
Отсюда следует, что
Примеры 2.12. Вычислить и рассмотреть с геометрической точки зрения следующие интегралы:
Решение.
Как и в предыдущем примере, вычисляя данные интегралы, фактически мы решили три геометрические задачи: вычислили площади фигур, изображённых на рисунках 2.20 – 2.22

Рис. 2.20

Рис. 2.21

Рис.2.22 Таким образом, если функция
Пример 2.13.Найти площадь фигуры, ограниченной линиями
Рис. 2.23 Решение.Из чертежа (рис. 2.23) видно, что искомая площадь
каждая из которых находится по геометрическому смыслу определенного интеграла. Решая систему
Окончательно Отметим, что данная задача может быть также решена другим способом. Сделаем сначала некоторые замечания общего характера. По определению определенного интеграла
Это равенство можно понимать так, что при построении интегральной суммы разбиению подвергается отрезок
Рис 2.24
Теперь возвращаясь к задаче нашего примера, можем записать:
Пусть функция
Рис.2.25
Отражая кривую
Рис. 2.26
Таким образом, если функция Пример 2.14.Найти площадь фигуры, ограниченной линиями
Рис. 2.27
Решение.Из рис. 2.27 видно, что искомая площадь
Окончательно Пусть на отрезке
Рис. 2.28
Площадь
Сделанные замечания позволяют дать еще одну геометрическую интерпретацию теоремы о среднем. Равенство (2.15) можно переписать в виде
т.е. теорема о среднем утверждает, что найдется такая точка
Приведем формулу, применение которой часто упрощает решение задач на вычисление площадей плоских фигур. Теорема 2.9.Пусть на отрезке
Проиллюстрируем теорему графически. Возможны несколько случаев расположения кривых на отрезке Случай 1.
откуда следует формула (2.27). Случай 2.
откуда следует (2.27). Случай 3.
Рис. 2.32
откуда следует (2.27). Случай 4.Общий случай (рис. 2.33) сводится к частным случаям, рассмотренным выше, если разбить отрезок
Рис. 2.33 Пример 2.15.Найти площадь фигуры, ограниченной линиями
Рис. 2.34
Решение. Найдем координаты точек пересечения параболы Воспользуемся формулой (2.27), полагая Абсциссы точек
Поиск по сайту: |




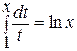 . Напомним, что в п.2.18 отмечалось, что возможен геометрический поход к определению логарифмической функции. Таким образом,
. Напомним, что в п.2.18 отмечалось, что возможен геометрический поход к определению логарифмической функции. Таким образом,




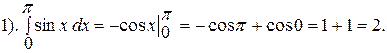
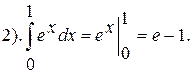
 =
= 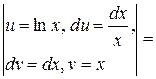





 неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке  , то в силу геометрического смысла определённого интеграла площадь
, то в силу геометрического смысла определённого интеграла площадь  под кривой
под кривой 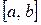 численно равна определённому интегралу
численно равна определённому интегралу  :
: (2.25)
(2.25)
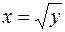 ,
,  ,
,  .
.
 равна разности двух площадей:
равна разности двух площадей: ,
, получаем, что точка
получаем, что точка  пересечения прямой
пересечения прямой 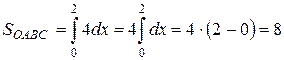 ,
, .
. .
. .
. оси ординат. Соответственно точки
оси ординат. Соответственно точки  - это оснащение , соответствующее данному разбиению. Поэтому, если
- это оснащение , соответствующее данному разбиению. Поэтому, если  на
на  численно равен площади
численно равен площади  и прямыми
и прямыми  ,
,  (рис. 2.24). (Другими словами, в данном случае площадь вычисляется посредством проецирования криволинейной трапеции на ось
(рис. 2.24). (Другими словами, в данном случае площадь вычисляется посредством проецирования криволинейной трапеции на ось 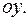 )
)

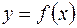 неположительна и непрерывна на
неположительна и непрерывна на  (рис. 2.25) . Выясним, какая связь в этом случае существует между площадью
(рис. 2.25) . Выясним, какая связь в этом случае существует между площадью  и интегралом
и интегралом 

 . Функция
. Функция  уже неотрицательна на
уже неотрицательна на 
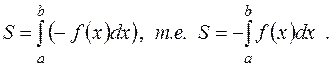
 .
. ,
, 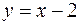 ,
,  .
.
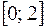 . Однако указанная ломаная не задается одним уравнением. Поэтому для нахождения
. Однако указанная ломаная не задается одним уравнением. Поэтому для нахождения  разобьем криволинейный треугольник
разобьем криволинейный треугольник  излома на ось абсцисс. Тогда
излома на ось абсцисс. Тогда  (рис. 2.27). Абсциссы точек
(рис. 2.27). Абсциссы точек  ,
,  ,
,  ,
,  соответственно предлагается провести самостоятельно).
соответственно предлагается провести самостоятельно). ,
,
 .
.
 фигуры, ограниченной графиком функции и осью
фигуры, ограниченной графиком функции и осью  складывается из трёх площадей:
складывается из трёх площадей:  , т.е. равна алгебраической сумме соответствующих определенных интегралов:
, т.е. равна алгебраической сумме соответствующих определенных интегралов: .
. ,
, , что после сдвига исходной кривой
, что после сдвига исходной кривой  для полученной кривой
для полученной кривой  площади частей криволинейной трапеции, расположенных выше и ниже оси
площади частей криволинейной трапеции, расположенных выше и ниже оси  , равны (например, на рис. 2.29
, равны (например, на рис. 2.29  ).
). Рис.2.29
Рис.2.29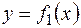 и
и  такие, что
такие, что  . Тогда площадь
. Тогда площадь  .
.
 (рис. 2.30).
(рис. 2.30). Рис. 2.30
Рис. 2.30 ,
, (рис. 2.31).
(рис. 2.31). Рис. 2.31
Рис. 2.31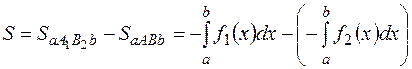 ,
, ,
,  (рис.2.32).
(рис.2.32).
 ,
,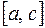 ,
,  ,
,  .
.
 ,
,  (рис.2.34).
(рис.2.34).
 . На отрезке
. На отрезке 
 .
. ,
,  .
.