 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема существования определённого интеграла
Приведённые примеры помогают осознать понятие определённого интеграла как предела интегральных сумм и оценить следующую важную теорему. Теорема 2.1. (Существование определённого интеграла).Если функция Приведём пример нахождения определённого интеграла на основании определения 2.1. Пример 2.3.Вычислить Пусть
Известно, что сумма квадратов первых
Поэтому
Отметим, что функция Приведённый пример показывает, что вычисление определённого интеграла как предела интегральных сумм оказалось возможным благодаря тому, что интегральную сумму удалось привести к виду, удобному для нахождения предела. Такая возможность существует далеко не всегда. Задача интегрирования конкретных функций с помощью определения 2.1 чрезвычайно сложна. Существует эффективный метод вычисления определённых интегралов с помощью так называемой формулы Ньютона-Лейбница, которая будет рассмотрена в п.2. 19.
2.10. Свойство аддитивности1) интеграла
Если функция
т.е. определённый интеграл по всему отрезку равен сумме интегралов по его частям. Пусть функция __________________________________________ (2.5) утверждает наличие следующего очевидного соотношения между этими площадями:
Рис. 2.9 ________________________________ 1)Аддитивность (от латинского additives – прибавляемый) – свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части. Например, аддитивность площади (объёма) означает, что площадь целой фигуры (целого тела) равна сумме площадей (объёмов) составляющих частей/ Отметим, что соотношение (2.9) справедливо при любом расположении точек
Рис. 2.10
Отсюда следует формула (2.5), утверждающая следующее очевидное соотношение между площадями:
Поиск по сайту: |
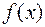 непрерывна отрезке
непрерывна отрезке 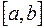 , то она интегрируема на этом отрезке, т.е. существует определённый интеграл
, то она интегрируема на этом отрезке, т.е. существует определённый интеграл 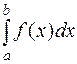 .
. .
. – дробление отрезка
– дробление отрезка  с помощью равноотстоящих точек:
с помощью равноотстоящих точек: 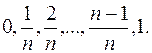 Выберем оснащение
Выберем оснащение 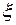 :
:  – совокупность правых концов частичных отрезков. Составим интегральную сумму
– совокупность правых концов частичных отрезков. Составим интегральную сумму .
. чисел натурального ряда вычисляется по формуле
чисел натурального ряда вычисляется по формуле .
.
 .
.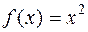 интегрируема в силу своей непрерывности (теорема 2.1.). Поэтому выбор дробления и оснащения не влияет на предел интегральной суммы.
интегрируема в силу своей непрерывности (теорема 2.1.). Поэтому выбор дробления и оснащения не влияет на предел интегральной суммы. , то имеет место формула
, то имеет место формула ,
,
 . Согласно геометрическому свойству определённого интеграла
. Согласно геометрическому свойству определённого интеграла  ,
,  ,
,  , где
, где  - площади под кривой
- площади под кривой 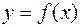 на отрезках
на отрезках  соответственно. Поэтому равенство
соответственно. Поэтому равенство .
.
 . Пусть
. Пусть 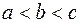 и функция
и функция  (рис. 2.10). Тогда
(рис. 2.10). Тогда .
.
 , где
, где 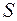 - площадь под кривой
- площадь под кривой