|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кристаллографические индексы. Период идентичности. Угол между кристаллографическими направлениями
Для определения положения узлов, направлений и плоскостей в кристалле используется система индексов. Поместим начало системы координат в один из узлов (произвольный) решетки, а направления координатных осей выберем вдоль основных трансляций (рис.1.1). Тогда положение любого узла однозначно определяется тройкой чисел m, n и p, если за единицы измерения выбрать параметры решетки а, b, c. Для указания индексов узла используются двойные квадратные скобки [[m n p]]. В кристаллах интересуют направления, проходящие через узлы. Для этого выбирается прямая, которая проходит через начало координат. Ее направление однозначно определяется индексами ближайшего к началу координат узла, который прямая пересекает. Индексы направления записывают в одинарные квадратные скобки [m n p]. Узлы пространственной решетки располагаются на группе равноудаленных плоскостей. Для определения таких групп используют индексы Миллера[6]. Процедура их введения заключается в следующем: определяются три отрезка А, B, C, которые отсекаются на осях каждой из плоскостей группы, в единицах кратных (или дробных) параметру решетки для каждой оси (рис.1.11); затем берут обратные величины
В гексагональной сингонии принято пользоваться системой координат из трех горизонтальных осей. Поэтому из четырех индексов (hkіl), используемых для обозначения плоскостей в гексагональной сингонии, третий не является независимым и определяется первыми двумя: Примеры обозначений некоторых направлений и плоскостей приведены на рис. 1.12 и рис. 1.13.
Определение межплоскостных расстояний является одной из важных задач кристаллографии. Расстояния определяются индексами плоскостей (hkl) и периодами кристаллической решетки. Формулы для межплоскостного расстояния имеют следующий вид:
для кубической сингонии;
для тетрагональной сингонии;
для гексагональной сингонии.
Совокупность физически (или кристаллографически) эквивалентных плоскостей обозначается фигурными скобками {hkl}, физически эквивалентных направлений – <mnp>. Так в кубической сингонии совокупность плоскостей куба {100} содержит шесть кристаллографически идентичных плоскостей: (100), ( Важнейшим признаком кристаллографически идентичных плоскостей есть то, что они имеют одинаковое межплоскостное расстояние. Периодом идентичности называют расстояние между ближайшими узлами вдоль определенной узловой прямой. В общем случае величина периода идентичности определяется как
Из этого выражения можно определить период идентичности для любого типа кристалла. Угол между двумя направлениями
Расписав скалярное произведение через проекции, получим:
В кубической сингонии это выражение для двух направлений
Объем элементарной ячейки, построенной на векторах
Получим выражения для объема элементарной ячейки любой сингонии. Для этого возведем в квадрат уравнение (1.10):
откуда
Воспользовавшись (1.7), получим из последнего равенства
Обратная решетка
В физике твердого тела при анализе многих явлений (дифракция рентгеновских лучей или электронов, рассеяние фотонов и т.д.) часто используют понятие обратной решетки. Для идеального монокристалла, который является трехмерным повторением некоторой структурной единицы, обратная решетка представляет собой бесконечное трехмерное распределение точек, расстояния между которыми обратно пропорциональны расстояниям между плоскостями прямой решетки. Поэтому условие брегговской дифракции может быть выражено через расстояния обратной решетки. Поскольку векторы в реальном пространстве имеют размерность длины, размерность векторов в обратном пространстве есть обратная длина. Векторы обратного пространства с точностью до масштабного множителя 2p можно сопоставить с волновыми векторами возбуждений, с помощью которых в физике твердого тела описывается движение электронов (или любых квазичастиц) в кристаллической решетке. Умножение координат обратного пространства на постоянную
где Отметим некоторые свойства обратной решетки. Каждый узел обратной решетки соответствует семейству параллельных плоскостей прямой решетки. Вектор обратной решетки Модуль вектора обратной решетки
Если в кристаллической решетке все углы прямые, то векторы элементарных трансляций Представление об обратной решетке оказывается очень эффективным в решении задач физики кристаллов и рентгеноструктурного анализа. Например, рентгенограмма есть взятая в некотором масштабе проекция обратной решетки кристалла.
1.8. Ячейки Вигнера-Зейтца[7] и зоны Бриллюэна[8]
Рассмотренные выше элементарные ячейки построены в базисе Браве. Однако иногда пользуются так называемой ячейкой Вигнера-Зейтца, параллельным переносом которой можно заполнить все пространство без промежутков. Для ее построения необходимо выбрать определенный узел в начале координат. Потом соединить этот узел отрезками с ближайшими узлами и через середины отрезков провести перпендикулярные к ним плоскости, которые ограничат определенную область пространства. Этот объем и представляет собой ячейку Вигнера-Зейтца (рис. 1.14). Эта ячейка содержит только один выбранный узел, а все точки внутри нее лежат ближе к центру ячейки, чем ко второму трансляционно эквивалентному узлу. Ячейка Вигнера-Зейтца для примитивной кубической решетки представляет собой куб, для ОЦК решетки – кубооктаэдр, для ГЦК – додекаэдр.
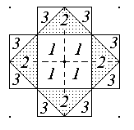
Если аналогичное построение выполнить в обратном пространстве, то образованные фигуры называют зонами Бриллюэна. Имеют место первая, вторая, третья и т.д. зоны Бриллюэна, образуемые в результате пересечения плоскостями отрезков, которые соединяют центральный узел с атомами первой, второй, третьей и т.д. координационных сфер. На рис. 1.15 показаны зоны Бриллюэна для двумерной решетки. Для примитивной кубической (ПК) решетки первая зона Бриллюэна является также примитивной кубической, для ОЦК решетки первой зоной Бриллюэна является додекаэдр, для ГЦК решетки – кубооктаэдр. Соотношение между формами прямой решетки, обратной решетки, ячейки Вигнера-Зейтца и зон Бриллюэна для трех кубических решеток приведено в табл.1.3.
Таблица 1.3. Форма прямой решетки, обратной решетки, ячейки Вигнера-Зейтца и зон Бриллюэна для кубических решеток
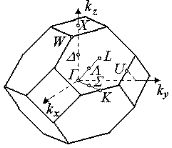
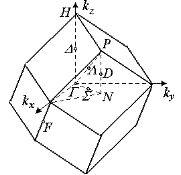
Одной из основных задач физики твердого тела является вычисление зависимости энергии носителей заряда от волнового вектора Не существует металлов и полупроводников с простой кубической решеткой, но она лежит в основе некоторых сплавов и соединений. Например, для b- латуни и хлористого цезия. Зона Бриллюэна для электронных состояний в таких кристаллах представляет собой простой куб (рис. 1.16, а). Для характерных точек зоны используют такие обозначения:
Для характерных точек зоны Бриллюена ГЦК структур используют следующие обозначения (рис.1.16, б):
Обозначение точек в зоне Бриллюэна ОЦК структур приведено на рис. 1.16, в.
Поиск по сайту: |
 и приводят их к общему знаменателю D. Целые числа
и приводят их к общему знаменателю D. Целые числа 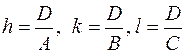 и будут представлять индексы Миллера для группы равноудаленных плоскостей, они заключаются в круглые скобки (hkl). Если плоскость пересекает какую-нибудь ось в области отрицательных значений (например, ось а), то индексы Миллера такой плоскости записываются в виде
и будут представлять индексы Миллера для группы равноудаленных плоскостей, они заключаются в круглые скобки (hkl). Если плоскость пересекает какую-нибудь ось в области отрицательных значений (например, ось а), то индексы Миллера такой плоскости записываются в виде 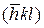 .
.
 . Часто им пренебрегают и вместо него ставят точку (h к. l).
. Часто им пренебрегают и вместо него ставят точку (h к. l).
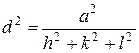 (1.3)
(1.3) (1.4)
(1.4)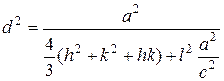 (1.5)
(1.5)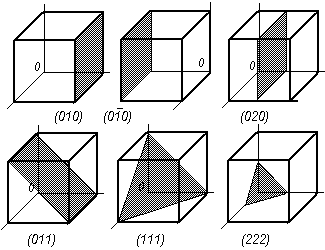
 00), (010), (0
00), (010), (0 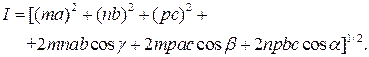 (1.6)
(1.6)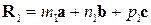 и
и 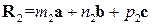 в общем случае определяется за формулой
в общем случае определяется за формулой . (1.7)
. (1.7) .(1.8)
.(1.8)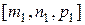 и
и  приобретает вид:
приобретает вид: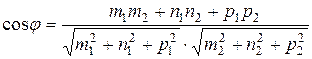 . (1.9)
. (1.9)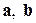 и
и  определяется смешанным произведением:
определяется смешанным произведением: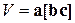 . (1.10)
. (1.10) ,
,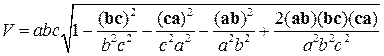 .
.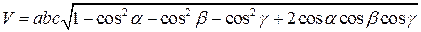 . (1.11)
. (1.11) переводит его в пространство импульсов. Для построения обратной решетки вводят вектора трансляции
переводит его в пространство импульсов. Для построения обратной решетки вводят вектора трансляции  , связанные с векторами трансляции прямой решетки соотношениями
, связанные с векторами трансляции прямой решетки соотношениями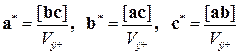 , (1.12)
, (1.12)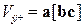 – объем элементарной ячейки.
– объем элементарной ячейки.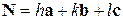 является перпендикулярным к плоскости с индексами
является перпендикулярным к плоскости с индексами 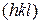 атомной решетки.
атомной решетки.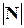 равняется обратному расстоянию между ближайшими плоскостями семейства
равняется обратному расстоянию между ближайшими плоскостями семейства 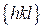 :
: . (1.13)
. (1.13)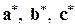 обратной решетки параллельны векторам
обратной решетки параллельны векторам 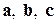 прямой решетки и обратны им по величине.
прямой решетки и обратны им по величине.
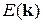 , однако это практически невозможно выполнить для всей зоны Бриллюэна. Поэтому вычисление проводят вдоль определенных направлений, которые имеют общепринятые обозначения (рис. 1.16). Центр зоны Бриллюэна всегда отмечают буквой
, однако это практически невозможно выполнить для всей зоны Бриллюэна. Поэтому вычисление проводят вдоль определенных направлений, которые имеют общепринятые обозначения (рис. 1.16). Центр зоны Бриллюэна всегда отмечают буквой  .
.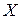 – центр квадратной грани;
– центр квадратной грани; – вершина куба;
– вершина куба;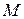 – середина ребра;
– середина ребра;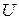 – середина ребра между шестиугольной и квадратной гранями;
– середина ребра между шестиугольной и квадратной гранями;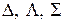 – середины расстояний
– середины расстояний  и
и 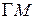 соответственно;
соответственно;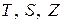 – середины расстояний
– середины расстояний 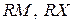 и
и 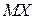 соответственно.
соответственно.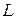 – центр шестиугольной грани;
– центр шестиугольной грани;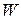 – вершина срезанного октаэдра;
– вершина срезанного октаэдра; – середина ребра между двумя шестиугольными гранями;
– середина ребра между двумя шестиугольными гранями; и
и 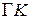 соответственно.
соответственно.