 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основні властивості подвійних інтегралів
1
2
3
Властивість 3
Рис 3.
Обчислення подвійних інтегралів в прямокутних координатах Обчислення подвійного інтеграла в прямокутних координатах по заданій області зводиться до обчислення так званих повторних інтегралів шляхом проектування області Область
Рис. 4. Перехід до повторного інтеграла пояснимо на задачі обчислення маси неоднорідної області. Нехай область Зафіксуємо точку
Далі, розглянемо паралельну осі
Щоб знайти масу всієї області
Порядок інтегрування можна змінити, якщо область
Рис. 5. Аналогічно попереднього випадку,
- маса елемента площею
Інтегруючи останній вираз по
Перехід від повторного інтеграла, що в правій частині (1), до повторного інтеграла в (2) називається зміною порядка інтегрування. На практиці з двох порядків (двох формул (1) чи (2)) вибирають такий, який вимагає менших обчислень.
Приклади. Знайти інтеграли 1.
Розв’язання.
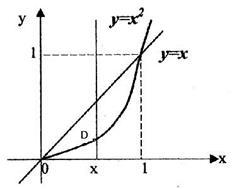
2. Розв’язання. Побудуємо область D (Рис.6). З рисунка видно, що Тому отримуємо:
Рис. 6.
Змінимо порядок інтегрування, спроектувавши область D на вісь Тоді
3. Розв’язанняПобудуємо границю області
Рис. 7. 1) Спроектуємо область Тоді
Отже, тут прийдеться обчислити два повторні інтеграли. 2) Спроектуємо область
За другим способом ми обчислювали тільки один повторний інтеграл. З а д а ч і. Обчислити повторні інтеграли.
Відповіді: 1. Обчислити подвійні інтеграли по областях які обмежені заданими лініями. 6. 7. 8. 9. 10. 11. Відповіді: 6.
4.4. Подвійні інтеграли в полярних координатах У деяких випадках, коли підінтегральна функція
Тоді має місце рівність:
рис. 8. Нехай промені
Якщо ж полюс міститься внутрі області
рис. 9. Приклад. Обчислити подвійний інтеграл.
де область Розв’язання. Перейдемо до полярних координат: В півкрузі
рис. 10.
Задача. Обчислити інтеграли 1. 2. 3. 4. 5. 6. Відповіді. 1.
Поиск по сайту: |
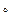 . Подвійнійний інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі подвійних інтегралів від кожної з цих функцій:
. Подвійнійний інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі подвійних інтегралів від кожної з цих функцій: .
.
 можна розбити на дві частини
можна розбити на дві частини 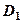 і
і  так, що вони не мають спільних внутрішніх точок
так, що вони не мають спільних внутрішніх точок 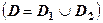 , то
, то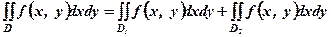
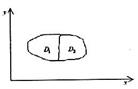
 або
або  .
. називається простою відносно осі
називається простою відносно осі  осі
осі 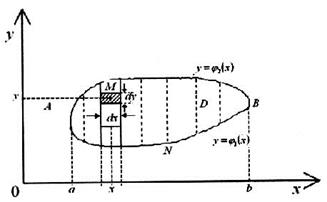
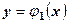 і
і  , які перетинаються в точках
, які перетинаються в точках 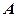 і
і 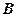 . Відрізок
. Відрізок  . У кожній точці
. У кожній точці  області
області 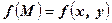 - густина розподілу маси. Знайти масу області
- густина розподілу маси. Знайти масу області 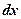 і
і 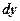 , що значення густини
, що значення густини  в точці
в точці 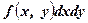 .
.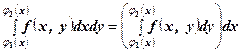 .
.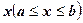 , тоді
, тоді . (1)
. (1) правидьна відносно осі
правидьна відносно осі 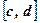 буде проекцією області
буде проекцією області 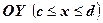 , область
, область 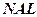 і
і 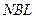 , які задаються відповідно рівняннями
, які задаються відповідно рівняннями  і
і 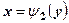 .
.
 . Масу смужки паралельної осі
. Масу смужки паралельної осі  :
: .
.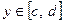 , отримаємо масу всієї області
, отримаємо масу всієї області 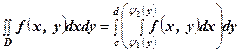 . (2)
. (2)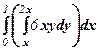 .
.
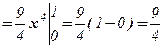 .
.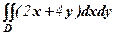 , де область D обмежена лініями
, де область D обмежена лініями 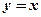 ,
, 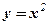 . Обчислення здійснити в одному і другому порядках.
. Обчислення здійснити в одному і другому порядках.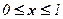 , а
, а  .
.

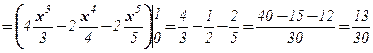 .
.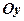 :
: 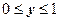 ,
, 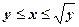 .
.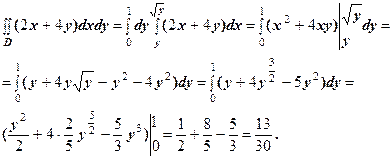
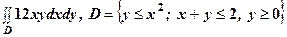 . З двох порядків інтегрування вибрати зручніший і обчислити.
. З двох порядків інтегрування вибрати зручніший і обчислити.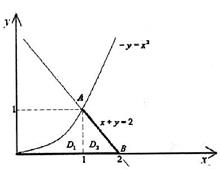
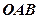 складається з двох ланок: дуги
складається з двох ланок: дуги  і відрізка
і відрізка 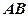 , які перетинаються в точці
, які перетинаються в точці 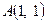 , то область
, то область  і
і  .
.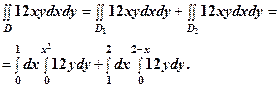 .
.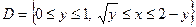 . Тоді
. Тоді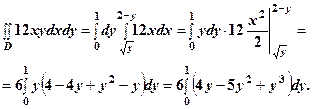
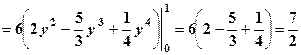 .
.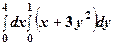 .
.
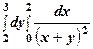 .
.
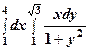 .
.
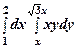 .
.
 .
.
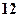 . 2.
. 2. 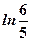 . 3.
. 3. 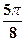 . 4.
. 4. 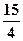 . 5.
. 5. 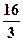 .
. .
.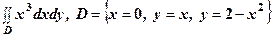 .
.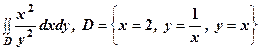 .
. .
. .
.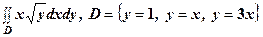 .
. . 7.
. 7.  . 8.
. 8. 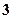 . 10.
. 10.  . 11.
. 11. 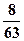 .
.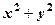 чи
чи 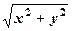 , або область інтегрування є круг чи частина круга, подвійний інтеграл легше обчислювати, якщо від прямокутних координат
, або область інтегрування є круг чи частина круга, подвійний інтеграл легше обчислювати, якщо від прямокутних координат 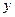 перейти до полярних
перейти до полярних 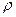 і
і  за формулами
за формулами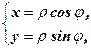
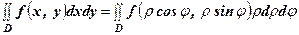 (1)
(1)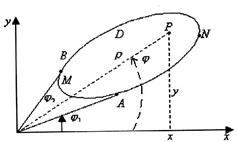
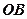 , які дотикаються границі області
, які дотикаються границі області 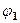 і
і 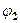
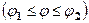 . Область
. Область  і
і 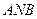 , рівняння яких в полярних координатах відповідно
, рівняння яких в полярних координатах відповідно  і
і 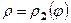
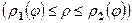 , тоді рівність (1) запишеться:
, тоді рівність (1) запишеться: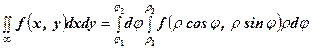 . (2)
. (2)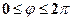 , а
, а 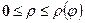 , де
, де  - рівняння границі області
- рівняння границі області 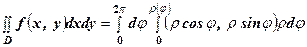 . (3)
. (3)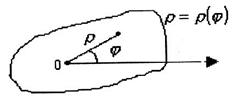
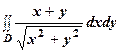 ,
,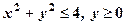 .
.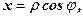
 . Запишемо рівняння півкола
. Запишемо рівняння півкола 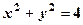 ,
, 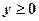 в полярних координатах:
в полярних координатах:  .
.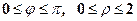 (див. рис. 10), тоді
(див. рис. 10), тоді

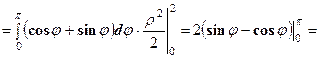
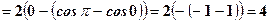 .
.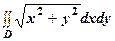 ; -
; - 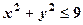 .
. ;
; 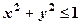 ,
, 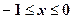 ,
, 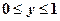 .
.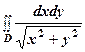 ;
; 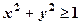 ,
, 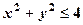 .
. ;
; 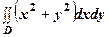 ;
;  .
. ;
; 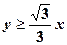 ,
, 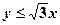 ,
, 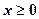 .
. . 2.
. 2. 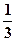 . 3.
. 3. 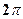 . 4.
. 4. 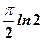 . 5.
. 5. 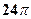 . 6.
. 6. 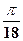 .
.