 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основні властивості невизначеного інтегралаСтр 1 из 4Следующая ⇒
II. Інтегральне числення Невизначений інтеграл Означення невизначенного інтеграла
Означення 1.Функція F(x) називається первісною функцією для функції f(x) на інтервалі (a, b), якщо F(x) – диференційовна на (a, b) i F¢(x)=f(x). Так, наприклад, для функцій Теорема 1. Якщо F(x) – первісна для функції f(x) на інтервалі (a, b), то F(x)+C – теж первісна, де С – довільна стала. Теорема 2. Якщо F1(x) i F2(x) – дві первісні для f(x) на інтервалі (a, b), то F1(x)–F2(x)=С на (a, b), де С– деяка стала. Означення 2.Довільна первісна для функції f(x) на інтервалі (a, b), називається невизначеним інтегралом і позначається символом
Якщо F(x) – одна із первісних функції f(x), то згідно означення
де символ Процес знаходження первісної називається інтегруванням. Згідно з (1) зв’язок між наведеними вище функціями
Зауваження. Інтеграли (1) – (4) входять до так званих основних табличних інтегралів. Теорема 3. Якщо f(x) – неперервна на інтервалі (a, b), то для неї існує первісна, а, отже, і невизначений інтеграл.
Основні властивості невизначеного інтеграла
5°. 6°. 7°. Якщо а) б)
Дамо формулювання наведених властивостей. 1 2 З точністю до сталого доданка виконуються подальші властивості. 3 4 Отже, із властивостей 1 5 6 Властивості 1 Нехай
Зупинимось ще на властивості 5
Отже, вирази Решта властивостей перевіряються аналогічно. Приклади. Знайти інтеграли.
=[власт 5
інт. (1), (4) і власт. 7 а) і б)]=
Таблиця основних невизначених інтегралів Таблиця 1
Таблиця 2 Це перетворення таблиці 1 за допомогою властивостей 7 а),б). (зберігаєтся нумерація таблиці 1) 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Таблица 3 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16.
Поиск по сайту: |
 ,
,  ,
,  ,
,  первісними відповідно є функції
первісними відповідно є функції  ,
,  ,
, 
 ,
,  , оскільки
, оскільки  ,
, 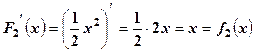 ,
,  ,
, 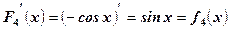 .
.
 (1)
(1) - знак інтеграла,
- знак інтеграла,  , - підінтегральна функція,
, - підінтегральна функція,  - підінтегральний вираз,
- підінтегральний вираз,  - довільна стала величина.
- довільна стала величина. ,
,  ,
,  ,
,  і відповідними їм первісними можна записати у вигляді інтегралів:
і відповідними їм первісними можна записати у вигляді інтегралів: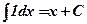 ; (1)
; (1) 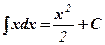 ; (2)
; (2)
 ; (3)
; (3)  . (4)
. (4) .
.
 .
.
 .
.
 .
.
 .
.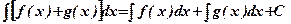 .
. 
 , то
, то ;
; .
. . Похідна від невизначеного інтеграла дорівнює підінтегральній функції.
. Похідна від невизначеного інтеграла дорівнює підінтегральній функції. плюс
плюс  на деякому інтервалі, тоді згідно з (1) маємо
на деякому інтервалі, тоді згідно з (1) маємо .
.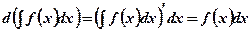 .
. ;
; .
. і
і  є первісними для однієї і тієї ж функції
є первісними для однієї і тієї ж функції  , вони можуть відрізнятись на сталий доданок
, вони можуть відрізнятись на сталий доданок  =[власт.6
=[власт.6 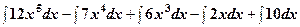 =
= -
-  =[за табл.. інтегр. (1)- (3)]=
=[за табл.. інтегр. (1)- (3)]= 
 +
+ 
 =
=  .
. =
= 

 =
=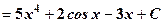 .
. =
=
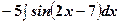 =[за табл..
=[за табл..
 .
.
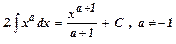 .
a – дійсне число
.
a – дійсне число

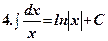



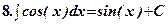
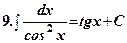 .
.
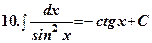 .
.





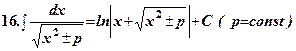
 .
. .
. .
. .
. .
. .
. .
.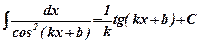 .
.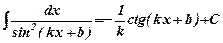 .
. .
.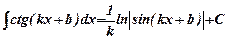 .
. .
.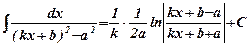 .
.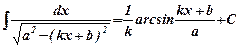 . 16.
. 16.  .
. .
. .
.
 .
. .
. .
.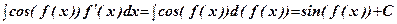 .
. .
. .
. .
.
 .
. .
.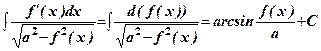 .
.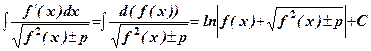 .
.