 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ⇐ ПредыдущаяСтр 4 из 4
Обчислення площі плоских фігур Якщо на відрізку
+ +
0 a - b x
Відомо, що визначений інтеграл на відрізку представляє собою площу криволінійної трапеції, обмеженої графіком функції f(x). Якщо графік розміщений нижче осі Ох, тобто f(x) < 0, тоді площа має знак “-“, якщо графік розміщений вище осі Ох, тобто f(x) > 0, тоді площа має знак “+”. Для знаходження сумарної площі використовується формула
Якщо функція Площу фігури, обмеженої кривими Коли криволінійна трапеція обмежена кривою, заданою параметрично прямими де Площа криволінійного сектора, обмеженого кривою, заданою в полярній системі координат неперервною функцією
r = f(j)
b О a обчислюється за формулою Приклад 1 Знайти площу фігури, обмеженої лініями y = x, y = x2, x = 2.
Шукана площа (заштрихована на малюнку) може бути знайдена по формулі:
Приклад 2 Обчислити площу фігури, обмеженої лініями:
Приклад 3 Знайти площу фігури, обмеженої параболами
Приклад 4 Обчислитиплощу фігури, обмеженої однією аркою циклоїди
і віссю абсцис. Приклад 5 Знайти площу фігури, обмеженої колом Користуючись вищенаведеним, обчислити площі фігур. 1. Обчислити площу фігур, обмежену лініями, рівняння яких 2. Обчислити площу фігури обмежену параболами 3. Обчислити площу фігури обмежену параболами 4. Найти площу фігур, на які парабола 5. Окружність 6. Обчислити площу фігури, що знаходиться всередині між лінією 7. Знайти площу фігури обмежену віссю координат і лінією 8. Знайти площу петлі лінії 9. Знайти площу фігури, обмежену замкнутою лінією 10. Знайти площу кінцевої частини фігури, обмеженої лініями 11. Обчислити площу фігури, обмеженої лініями 12. Обчислити площу криволінійного трикутника, обмеженого віссю ординат і лініями 13. Обчислити площу фігури, обмеженою астроїдою 14. Знайти площу петлі лінії 1) 2) 15. Знайти площу фігури обмеженої лінією 16. Знайти площу частини фігури, обмеженої лінією
В наступних задачах зручно перейти попередньо до полярних координат. 17. Знайти площу фігури, обмеженою лемніскатою Бернуллі 18. Знайти площу фігури, обмеженої лінією 19. Знайти площу фігури, яка знаходиться між лінією 20. Для лінії
Об’єм тіла виражається за допомогою інтеграла де Об’єм
x виражається інтегралом Якщо криволінійна трапеція обмежена графіком неперервної функції Об’єм тіла Якщо крива задана параметрично або в полярних координатах, тоді необхідно зробити відповідну заміну змінних у вказаних формулах. Приклад 1 Знайти обєм кулі радіуса R.
R у
-R 0 x R x
В поперечному перерізі кулі отримуємо кола змінного радіусу у. В залежності від поточної координати х цей радіус виражається по формулі Тоді функція площі перетинів має вид: Q(x) = Отримаємо обєм кулі:
Приклад 2
Знайти обєм довільної піраміди з висотою Н і площею основи S.
Q S
x H x
При перетині піраміди площинами, перпендикулярними висоті, в перетині отримаємо фігури, подібні основі. Коефіцієнт подібності цих фігур рівний відношенню x/H, де х – відстань від площини перетину до вершини піраміди. З геометрії відомо, що відношення площ подібних фігур дорівнює коефіцієнту подібності в квадраті, тобто
Звідси отримаємо функцію площ перетинів:
Знайдемо об’єм піраміди:
Приклад 3 Знайти об’єм тіла, утвореного обертанням навколо осі
Приклад 4 Обчислити об’єм тіла, утвореного обертанням фігури, обмеженої пів кубічною параболою
Приклад 5 Знайти об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої лініями Обчислити об’єми фігур, користуючись даними формулами. 1. Фігура, обмежена гіперболою 2. Знайти об’єм тіла, отриманого обертанням навколо осі абсцис трапеції, що лежить на осі 3.Знайти об’єм тіла, отриманого обертанням фігури, обмеженої параболою 4. Знайти об’єм тіла, отриманого обертанням навколо осі абсцис фігури, обмеженої лінією: 1) 5. Знайти об’єм тіла, отриманого при обертанні астроїди 6. Лінія 7. Знайти об’єм тіла, обмеженого поверхнею, яка виходить при обертанні тактриси 8. Обчислити об’єм тіл, обмежених параболоїдом 9. Знайти об’єм тіла, обмеженого параболоїдом
Якщо плоска крива задана рівнянням де Якщо крива задана рівняннями в параметричній формі де Якщо гладка крива задана рівнянням де Довжину дуги гладкої просторової кривої, заданої рівняннями обчислюється за формулою Приклад 1 Знайти довжину кола, заданого рівнянням x2 + y2 = r2.
Спосіб Виразимо з рівняння змінну у: Знайдемо похідну Тоді Отже, S = 2pr. Отримали загальновідому формулу довжини кола.
Спосіб Якщо представити задане рівняння в полярній системі координат, тоді отримаємо: r2cos2j + r2sin2j = r2, тобто функція r = f(j) = r,
Приклад 2 Знайти довжину кривої
від
Приклад 3 Знайти довжину дуги спіралі Архімеда
Приклад 4 Знайти довжину дуги кривої
Користуючись приведеними формулами, обчислити довжини наступних ліній. 1. Обчислити довжину дуги ланцюгової лінії 2. Обчислити довжину дуги лінії 3.Обчислити довжину дуги пів кубічної параболи 4.Обчислити довжину петлі лінії 5.Обчислити довжину лінії 6. Обчислити довжину лінії 7. Обчислити довжину дуги лінії (від ). 8. Обчислити довжину петлі лінії 9. Обчислити довжину кардіоїди 10. Знайти довжину лінії заданої рівнянням 11. Обчислити довжину дуги лінії
Площа поверхні, утвореної обертанням навколо осі
А
xi х
виражається інтегралом який зручно записувати у формі Якщо дуга задана параметричними рівняннями то площа поверхні обертання обчислюється за формулою Приклад 1 Знайти площу поверхні тора, утвореного обертанням кола
Приклад 2 Обчислити площу поверхні, утвореної обертанням кардіоїди
навколо осі абсцис.
Для самостійного опрацювання матеріалу розв’язати наступні задачі. 1. Обчислити площу поверхні, утвореної обертанням астроїди 2.Обчислити площу поверхні, утвореної обертанням навколо осі 3. Обчислити площу поверхні, утвореної обертанням частини кривої 4. Обчислити площу поверхні еліпсоїда, утвореного обертанням еліпса 5. Обчислити площу поверхні, утвореної обертанням еліпса 6.Знайти площу поверхні, утвореної обертанням навколо осі 7. Обчислити площу поверхні, утвореної обертанням навколо осі 8. Обчислити площу поверхні, утвореної обертанням лемніскати Відповіді на приклади
Розділ 1 1. 3. 4. 6. 8. 1. 4. 7. 16. 17. 20. 1. 4. 6. 7. 9. 11. 14. 1. 3. 4. 5. 1. 1. 3. 7. 10. 11. 12. 14. 18. 19. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 1. 2.
4. +C 5. 5. 7. 10. 1. 3. 4. 1. 2. 3. 4. 5. 6. 7. 8. 9. 11. 12. 13. 14. 15. 16. 17. 20. 1. 4. 7. 9. 1. 3. 4. 5. 6. 8. 1. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 1. 3. 5. 6. 8. 9. 10. 11. 12. 13. 14. 17. 20. 21. 22. 23. 24. 25. 26. 27. 28. 30. 31. 32. 33. 34. 35. 36. 37. 38. Розділ 2 1. 2. 3. 4. 1. 5. 13. 1. 7+2 ln 2 2. 7. 11. 1. 8. 10. 1. 0.6938 2. 1.2038 3. а) 0.601 б) 0.7462 4. 0.96 1. 12. При 13. 1) При 14. 22. 27. 31. Розбігається. 32. Сходиться. 33. Розбігається. 34. Сходиться. 35.Розбігається. 36. Сходиться. 37. 38. 8/3. 39. 1. 40. 2. 41. 44. 47. Сходиться. 48. Розходиться. Розділ 3 1. 5. 6.
Поиск по сайту: |
 функція
функція  неперервна і
неперервна і  , то площу криволінійної трапеції, обмеженої кривою
, то площу криволінійної трапеції, обмеженої кривою  ,
,  ,
,  , знаходять за формулою
, знаходять за формулою 
 .
. .
. .
. і
і  і прямими
і прямими  , знаходять за формулою
, знаходять за формулою .
. ,
,  ,
, , то її площа обчислюється за формулою
, то її площа обчислюється за формулою  ,
, ,
,  і
і  на відрізку
на відрізку  .
. і променями
і променями  та
та  ,
, 
 .
.



 (од2)
(од2) ,
,  .
. ,
, 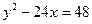 .
. ,
, і кардіоїдою
і кардіоїдою  (ззовні кардіоїди).
(ззовні кардіоїди). і
і  .
.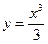 .
. ділить окружність
ділить окружність 
 розбивається гіперболою
розбивається гіперболою  на три частини. Знайти площу цих частин.
на три частини. Знайти площу цих частин. і параболою
і параболою  .
. .
.

 i
i 
 і
і 
 ,
,  .
. ,
,  .
. ,
,  ;
;  ,
, 

 , яка лежить за межами лінії
, яка лежить за межами лінії  .
.

 і її асимптотою.
і її асимптотою. знайти площу петлі і площу фігури, яка знаходиться між лінією і її асимптотою.
знайти площу петлі і площу фігури, яка знаходиться між лінією і її асимптотою. ,
, - площа перетину тіла площиною, перпендикулярної до осі
- площа перетину тіла площиною, перпендикулярної до осі  ,
,  і
і  - ліва і права границі зміни
- ліва і права границі зміни  тіла, утвореного обертанням навколо осі
тіла, утвореного обертанням навколо осі  , віссю абсцис і прямими
, віссю абсцис і прямими 
 y = f(x)
y = f(x) .
.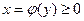 і прямими
і прямими  ,
,  ,
,  , то об’єм тіла, утвореного обертанням даної трапеції навколо осі
, то об’єм тіла, утвореного обертанням даної трапеції навколо осі  , знаходять за формулою
, знаходять за формулою  .
. і
і 
 і прямими
і прямими  .
. y
y .
. .
.
 .
.




 .
. , віссю абсцис і прямою
, віссю абсцис і прямою  , навколо осі
, навколо осі  ,
,  ,
,  і прямою
і прямою  ,
,  , обертається навколо осі абсциси. Найти об’єм тіла обертання.
, обертається навколо осі абсциси. Найти об’єм тіла обертання. .
. 
 і віссю абсцис, навколо осі ординат.
і віссю абсцис, навколо осі ординат. ; 2)
; 2)  .
. навколо своєї осі симетрії.
навколо своєї осі симетрії. обертається навколо своєї асимптоти. Знайти об’єм тіла, обмеженого поверхнею, яка виходить в результаті цього обертання.
обертається навколо своєї асимптоти. Знайти об’єм тіла, обмеженого поверхнею, яка виходить в результаті цього обертання. ,
,  навколо її асимптоти.
навколо її асимптоти. і еліпсоїдом
і еліпсоїдом 
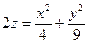 і конусом
і конусом  .
. і похідна
і похідна  неперервна, тоді довжина дуги цієї кривої виражається через інтеграл:
неперервна, тоді довжина дуги цієї кривої виражається через інтеграл: ,
, ,
,  і похідні
і похідні  ,
,  неперервні на відрізку
неперервні на відрізку  , тоді довжина дуги кривої обчислюється за допомогою інтегралу
, тоді довжина дуги кривої обчислюється за допомогою інтегралу ,
, і
і  - значення параметра
- значення параметра  , що відповідають кінцям дуги (
, що відповідають кінцям дуги (  .
. кривої виражається через наступний інтеграл:
кривої виражається через наступний інтеграл: ,
,  і
і  - значення полярного кута
- значення полярного кута  на кінцях дуги (
на кінцях дуги (  .
. ,
,  .
.


 тоді
тоді .
.
 до
до  .
. , яка лежить усередині кола
, яка лежить усередині кола  .
. ,
,  ,
,  від
від  .
. (від
(від  до
до  ).
). до
до  ).
). , що знаходиться всередині параболи
, що знаходиться всередині параболи  .
. .
.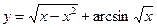 .
. ,
,  .
. ,
,  , від
, від  до
до  .
. ,
,  .
. .
. .
. ,
,  від початку координат до найближчої точки с вертикальною дотичною.
від початку координат до найближчої точки с вертикальною дотичною. кривої
кривої  Мi B
Мi B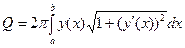 ,
, , де
, де  - диференціал довжини дуги.
- диференціал довжини дуги. ,
, 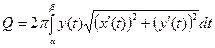 .
. навколо осі абсцис.
навколо осі абсцис.
 , утвореного кривими
, утвореного кривими  .
. , навколо осі
, навколо осі  навколо осі
навколо осі 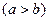 .
. навколо осі
навколо осі 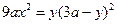 .
. .
. навколо полярної осі.
навколо полярної осі. . 2.
. 2. 

 5.
5. 
 7.
7. 
 9.
9. 
 2.
2.  3.
3. 
 5.
5.  6.
6. 
 8.
8.  9.
9.  10.
10.  11.
11.  12.
12.  13.
13.  14.
14.  15.
15. 

 18.
18.  19.
19. 

 при
при  2.
2.  3.
3. 
 5.
5. 

 8.
8. 
 10.
10. 
 12.
12.  13.
13. 

 2.
2. 



 2.
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8. 
 2.
2. 
 4.
4.  5.
5.  6.
6. 
 8.
8.  9.
9. 


 13.
13. 
 15.
15.  16.
16.  17.
17. 

 20.
20. 











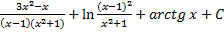





 3.
3. 
 , де u=
, де u= 
 6.
6. 
 8.
8.  9.
9. 

 2.
2. 
 +C
+C 5.
5.  де
де 





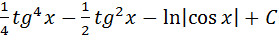


 10.
10. 



 , для значень x які задовільняють нерівність
, для значень x які задовільняють нерівність  , і
, і 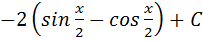 , для значень x які задовільняють нерівність
, для значень x які задовільняють нерівність 


 . 18.
. 18.  . 19.
. 19. 
 21.
21.  .
.  2.
2.  3.
3. 
 5.
5.  6.
6. 
 8.
8. 
 10.
10. 
 2.
2. 
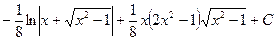


 7.
7. 

 2.
2. 



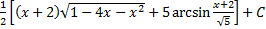





 13.
13. 
 2.
2. 
 4.
4. 

 7.
7. 






 15.
15.  16.
16. 
 18.
18.  19.
19. 

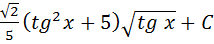

 .
.


 .
. . 29.
. 29. 
 , де
, де  , якщо
, якщо 
 , де
, де 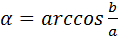 якщо
якщо 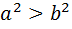



 .
. +
+ 







 2.
2.  3.
3.  4.
4. 
 6.
6.  7. 2 8.
7. 2 8.  9.
9.  10.
10.  11.
11.  12. 2
12. 2 14. -0.083… 15.
14. -0.083… 15. 
 3.
3.  . Покласти
. Покласти  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  .
. . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  .
. - найбільше значення,
- найбільше значення,  найменше значення. 12. 13.
найменше значення. 12. 13. 2.
2.  3. 1 4.
3. 1 4.  5.
5.  6.
6.  7. a)
7. a) 
 9.
9. 
 11.
11.  12.
12.  13.
13.  14.
14.  16.
16.  17.
17.  18.
18.  19.
19.  20.
20.  21.
21. 
 2. Розходиться 3.
2. Розходиться 3.  4.
4.  5.
5.  6.
6.  7. Розходиться 8. 2 9.
7. Розходиться 8. 2 9.  11.
11. 
 1 сходиться, при
1 сходиться, при 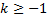 розходиться.
розходиться. сходиться, при
сходиться, при  розходиться. 2)
розходиться. 2)  , якщо
, якщо  15.
15.  16.
16.  17.
17.  18.
18.  19. 0 20.
19. 0 20.  21.
21.  Інтегрувати по чястинам
Інтегрувати по чястинам 24.
24.  26.
26. 
 28.
28.  29.
29.  .
. . 42.
. 42.  . 43. 10/7
. 43. 10/7 45. Розходиться. 46. Сходиться.
45. Розходиться. 46. Сходиться. 2.
2.  4.
4. 

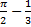 7.
7.  8.
8.  9.
9.  10.
10.  11.
11.  12.
12.  13.
13.  14.
14.  15.
15.  17.
17.  18.
18.