 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Властивості визначеного інтеграла. 1. Якщо всюди на відрізку маємо , то
1. Якщо всюди на відрізку 2. Якщо всюди на відрізку (монотонність визначеного інтеграла). 3. Якщо функція 4. Якщо (оцінка інтеграла по області). 5. Якщо функція (теорема про середнє значення функції). Число називається середнім значенням функції 6. Якщо функція є первісною для функції 7. Якщо функції Виходячи з означення визначеного інтеграла і розбиваючи проміжок інтегрування на
Приклад 1
Розіб’ємо проміжок
де
По формулі суми арифметичної прогресії
Приклад 2
Розіб’ємо проміжок
Враховуючи, що
Приклад 3 Розбиваючи проміжок інтегрування на
Користуючись викладеним вище обчислити наступні інтеграли. 1.Обчислити, виходячи з визначення, інтеграл
2.Користуючись визначенням, обчислити інтеграл
3.Обчислити, виходячи з визначення, інтеграл
4.З допомогою граничного переходу від інтегральних сум обчислити інтеграл
розбиваючи відрізок а) на рівні частини; б) точками, що утворюють геометричну прогресію, причому в кожному з розбиттів в якості 1) ліві кінці відрізків, 2) праві кінці відрізків, 3) середини відрізків
Якщо Користуючись формулою Ньютона-Лейбніца та правилами інтегрування, викладеними в розділі 1, обчислити наступні інтеграли.
Приклад 1
Згідно правил інтегрування, викладених в п.1, 2, отримаємо
Приклад 2
Провівши деякі перетворення та використовуючи інваріантність диференціала отримаємо
При зміні місцями меж інтегрування, перед інтегралом з’явиться знак «-», тобто
Приклад 3
Внісши
Приклад 4
Аналогічно попередньому, вносячи
Приклад 5
Розкладемо підінтегральний вираз на прості дроби:
і далі, наш інтеграл набуде вигляду
Обчислити наступні інтеграли. 1. 3. 4. 6. 7. 9. 10. 12. 13. 15.
Заміна змінної Якщо функція Приклад 1 При заміні змінної у визначеному інтегралі варто пам’ятати про те, що функція, яка вводиться, (в даному випадку це функція sin) повинна бути неперервною на відрізку інтегрування. В іншому випадку, формальне застосування формули приводить до абсурду. Приклад 2 Якщо обчислити наступний інтеграл, отримаємо
З іншого боку, якщо застосувати тригонометричну підстановку,
Тобто, два способи обчислення інтеграла дають різні результати. Це відбувається тому, що не був врахований той факт, що введена змінна tgx має на відрізку інтегрування розрив (в точці х = p/2). Тому в даному випадку таку підстановку застосовувати неможливо. При заміні змінної у визначеному інтегралі потрібно уважно слідкувати за виконанням перерахованих вище умов.
Приклад 3 Провівши заміну, обчислити інтеграл
Введемо наступну заміну
Проведемо перерахунок меж інтегрування
Отримаємо наступний інтеграл:
Як видно, підінтегральний вираз на всьому проміжку інтегрування немає розривів, тобто заміна має місце.
Приклад 4 Обчислити наступний інтеграл
Введемо наступну заміну:
Проведемо перерахунок меж інтегрування:
Провівши деякі перетворення, отримаємо
Приклад 5 Провівши відповідну заміну, обчислити інтеграл
Перед проведенням заміни, зробимо деякі перетворення підінтегральної функції:
Проведемо наступну заміну:
Також зробимо перерахунок меж інтегрування
Отримаємо
Заміна змінної у визначеному інтегралі 1. 3. 4. 6. 7.
9.Розв’язати рівняння 10. Розв’язати рівняння 11. Знайти найбільше і найменше значення функції В даних задачах не обчислюючи інтегралів довести справедливість рівнянь 12. 13.
Якщо функції
Користуючись вищенаведеною формулою та методами інтегрування, наведеними в розд.1 обчислити наступні інтеграли.
Приклад 1
Згідно правила інтегрування частинами проведемо заміни
і застосуємо формулу інтегрування частинами
Підставивши межі, остаточно отримаємо
Приклад 2
Проведемо відповідні заміни
Застосувавши формулу інтегрування частинами, отримаємо
І, підставляючи межі, остаточно отримаємо
Приклад 3
Згідно правила інтегрування частинами проведемо заміни
По формулі інтегрування частинами матимемо:
Приклад 4
Проведемо відповідні заміни
Застосувавши формулу інтегрування частинами, отримаємо
І остаточно, підставивши межі, отримаємо
Приклад 5
Як ми знаємо з розд.1, щоб обчислити даний інтеграл, необхідно, проінтегрувавши його два рази по частинах, розв’язати рівняння відносно інтеграла. Проведемо першу заміну:
За формулою інтегрування частинами, отримаємо
Проінтегруємо частинами вдруге:
Перенесемо інтеграл вліво і розв’яжемо рівняння відносно інтеграла.
І остаточно
Застосовуючи формулу інтегрування частинами та використовуючи зразки прикладів, розв’язаних вище, розв’язати наступні задачі: 1. 3. 4. 6. 7. Скласти рекурентні формули для обчислення інтегралів a) b) c) 8. Скласти рекурентну формулу та вирахувати інтеграл 9. Доказати рекурентну формулу
(n-ціле додатне число) і вирахувати за її допомогою інтеграл
10. Доказати, що якщо
Різні задачі 11. Вирахувати середнє значення функції 12. Вирахувати середнє значення функції 13. Вирахувати середнє значення функції і 14. Знайти середнє значення функції Обчислити інтеграли: 15. 17. 18. 20. 21. 22.
Формула прямокутників
M
m
0 a xi b х Якщо відомі значення функції f(x) в деяких точках x0, x1, … , xm, тоді за функцію, «близьку» до f(x), можна взяти многочлен Р(х) степені не вище m, значення якого у вибраних точках дорівнюють значенням функції f(x) в цих точках. Якщо розбити відрізок інтегрування на n рівних частин y0 = f(x0), y1 = f(x1), …. , yn = f(xn). Утворимо суми: y0Dx + y1Dx + … + yn-1Dx y1Dx + y2Dx + … + ynDx Це, відповідно, нижня і верхня інтегральні суми. Перша відповідає вписаній ломаній, друга – описаній. Тоді або Будь-яка з цих формул може використовуватись для наближеного обчислення визначеного інтеграла і називається формулою прямокутників. В загальному випадку, можна записати наступне де Формула трапецій Ця формула є більш точною в порівнянні з формулою прямокутників. Підінтегральну функцію в цьому випадку заміняємо на вписану ломану.
y1 у2 уn a x1 x2 b x Геометрично площа криволінійної трапеції заміняється сумою площ вписаних трапецій. Очевидно, що чим більше взяти точок розбиття інтервалу, з тим більшою точністю буде обчислений інтеграл. Площі вписаних трапецій обчислюються по формулах: Після приведення схожих доданків, отримаємо формулу трапецій: де Формула Сімпсона Розділимо відрізок інтегрування [a, b] на парну кількість відрізків (2m). Площа криволінійної трапеції, обмеженої графіком функції f(x) замінимо на площу криволінійної трапеції, обмеженої параболою другої степені з віссю симетрії, паралельної осі Оу, що проходить через точки кривої із значеннями f(x0), f(x1), f(x2). Для кожної пари відрізків побудуємо таку параболу:
0 х0 х1 х2 х3 х4 х Рівняння цих парабол мають вид Ax2 + Bx + C, де коефіцієнти А, В, С можна легко знайти по трьох точках перетину параболи з вихідною кривою. Позначимо Якщо прийняти х0 = -h, x1 = 0, x2 = h, тоді Тоді рівняння значень функції мають вигляд: Із врахуванням цього: Тоді обчислення Тоді Додавши ці вирази, отримаємо формулу Сімпсона: Чим більше взяти число І в скороченому виді де Формула Тейлора. Крім вище перерахованих способів, можна обчислити значення визначеного інтеграла за допомогою розкладу підінтегральної функції в степеневий ряд. Принцип цього методу полягає в тому, щоб замінити підінтегральну функцію по формулі Тейлора і почленно проінтегрувати отриману суму. Приклад 1 З точністю до 0,001 обчислити інтеграл
Так як інтегрування проводиться в околі точки х=0, тоді можливо скористатись для розкладу підінтегральної функції формулою Маклорена. Розклад функції cosx має вид:
Знаючи розклад функції cosх легко знайти функцію 1 – cosx:
В цій формулі сумування проводиться по п від 1 до нескінченності, а в попередній – від 0 до нескінченності. Це – не помилка, так виходить в результаті перетворення.
Тепер представимо у вигляді ряду підінтегральний вираз.
Тепер представимо наш інтеграл у вигляді:
Отже,
І остаточно отримаємо
Як бачимо, абсолютна величина членів ряду дуже швидко зменшується, і необхідна точність досягається вже в третьому члені розкладу.
Для довідки: Точне (або – більш точне) значення цього інтегралу: 0,2482725418… Приклад 2 Обчислити наближене значення визначеного інтегралу
за допомогою формули Сімпсона, разбивши відрізок інтегруровання на 10 частин.
По формулі Сімпсона отримаємо:
Точне значення цього інтеграла – 91.173.
Як бачимо, навіть при достатньо великому кроці розбиття точність отриманого результату цілком задовільна. Для порівняння, застосуємо до цієї ж задачі формулу трапецій:
Формула трапецій дала менш точний результат в порівнянні з формулою Сімпсона.
1.Обчислити наближено інтеграл 2.Обчислити по формулі Сімпсона інтеграл 3.Обчислити інтеграли: а) б) 4. По формулі Сімпсона обчислити наближене значення інтеграла
якщо підінтегральна функція задана наступною таблицею:
Поиск по сайту: |
 маємо
маємо 
 , то
, то  .
.

 інтегрована на відрізку
інтегрована на відрізку  .
. і
і  - відповідно найбільше і найменше значення функції
- відповідно найбільше і найменше значення функції 
 , що
, що 


 .
. і
і  диференційовані в точці
диференційовані в точці  і
і  неперервна при
неперервна при 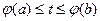 , то
, то .
. рівних частин, обчислити наступні інтеграли.
рівних частин, обчислити наступні інтеграли.
 на
на  , і замінимо інтеграл, згідно означення, інтегральною сумою
, і замінимо інтеграл, згідно означення, інтегральною сумою
 , тобто отримаємо
, тобто отримаємо
 ,
,
 .
.
 на
на  , і замінимо інтеграл, згідно означення, інтегральною сумою
, і замінимо інтеграл, згідно означення, інтегральною сумою
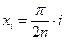 , отримаємо
, отримаємо
 .
. .
. .
.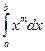 .
. .
. ,
,
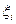 вибирати
вибирати .
. є якою-небудь первісною від неперервної функції
є якою-небудь первісною від неперервної функції  ,
,  , то справедлива формула Ньютона-Лейбніца
, то справедлива формула Ньютона-Лейбніца .
.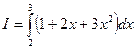

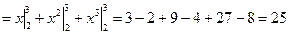 .
.


 .
.
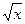 із знаменника під диференціал та застосовуючи інваріантність диференціала, отримаємо
із знаменника під диференціал та застосовуючи інваріантність диференціала, отримаємо
 .
.
 під диференціал та використовуючи правила інтегрування, отримаємо
під диференціал та використовуючи правила інтегрування, отримаємо
 .
.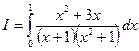
 ,
,

 .
. 2.
2. 

 5.
5. 

 8.
8. 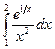

 11.
11. 
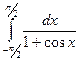
 14.
14. 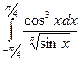
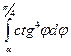
 і її похідна
і її похідна 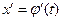 неперервні на відрізку
неперервні на відрізку  , причому
, причому  ,
,  , то справджується рівність
, то справджується рівність .
.
 .
.

 . Тоді
. Тоді ,
,  ,
,  .
.

 ;
;
 .
.
 .
.
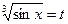 ,
,  ,
,  ,
,  .
.
 ;
;
 .
.

 .
.

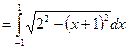 .
. ,
, 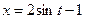 ,
, 
 .
.
 ;
;
 .
.

 .
. 2.
2. 

 5.
5. 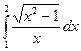
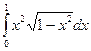
 8.
8. 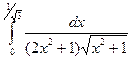


 на відрізку [-1, 1].
на відрізку [-1, 1].

 ,
,  та їхні похідні
та їхні похідні  і
і  неперервні на відрізку
неперервні на відрізку  .
.


 .
.



 .
.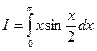

 .
.





 .
.
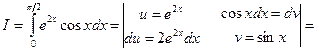




 .
.
 .
. 2.
2. 

 5.
5. 

 і
і  (n-ціле додатне число або нуль) та обчислити інтеграли:
(n-ціле додатне число або нуль) та обчислити інтеграли: ;
; ;
; .
. (n-ціле додатне число).
(n-ціле додатне число). ,
, .
. , то
, то  (m-ціле достатнє число).
(m-ціле достатнє число). на відрізку [1;4].
на відрізку [1;4]. на відрізку [1;1,5].
на відрізку [1;1,5]. і
і  на відрізку
на відрізку 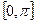 .
. на відрізку [0;2].
на відрізку [0;2].

 19.
19. 
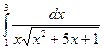
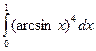
 23.
23. 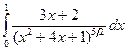
 y
y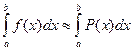
 , тоді отримаємо:
, тоді отримаємо: ,
,  -
-  ,
, ,
,  .
. у
у 

 ,
, .
. у
у
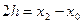 .
.
 .
. 
 .
. будемо проводити за формулою
будемо проводити за формулою 


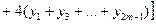
 ,
, .
.











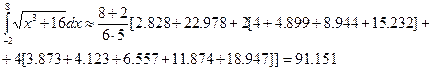

 по формулі трапецій при
по формулі трапецій при 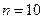 .
. з точністю до
з точністю до 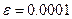 .
. з точністю до
з точністю до  по формулі Сімпсона;
по формулі Сімпсона; з точністю до
з точністю до  ,
,