 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Властивості визначеного інтеграла
Підсумовування нескінченно малих Нехай задано неперерву функцію на відрізку [a; b] і F(x) —будь-яка її первісна. Розіб’ємо відрізок [a; b] на n частин і утворимо різницю F(b) – F(a) (1) значень первісної на його кінцях. Різниця (1) дорівнює сумі таких самих різниць, складених для відрізків, на які розбито даний:
Рис. 2.1
За теоремою Лагранжа про скінченний приріст маємо: F(хі) – F(хі – 1) = (хі – хі – 1)F¢(xi – 1), де xi Î [хі; хі–1] (рис. 2.1). Позначивши хі – хі–1 = D хі–1 і врахувавши, що F¢(xi–1) = f(xi–1), рівність (2) подамо так: F(b) – F(a) = f(x0)Dх0 + f(x1)Dх1 + … + f(xn–1)Dхn – 1. (3) Залежність (3) справджується лише для значень x0, x1, … xn, які задовольняють теорему Лагранжа. Але коли необмежено збільшувати кількість n частин відрізка [a; b] так, щоб довжина відрізка Dхі – 1 прямувала до нуля, то рівність (3) виконуватиметься і різниця F(b) – F(a) буде сумою нескінченної кількості спадних доданків:
Рівність (3) справджується не лише за певного, а й за будь-якого вибору точок x0, x1, … xn–1, тому (4) є формулою суми нескінченно малих,яку вивели Лейбніц і Ньютон. 55. Поняття визначеного інтеграла. Означення. Сума
називається інтегральною сумою, або сумою Рімана. Означення. Скінченна границя І суми s при
де а, b — відповідно нижня та верхня межі інтегрування, ò — знак інтеграла, введений Лейбніцем. (Лейбніц увів знак інтеграла ò як витягнуту букву S, що позначає підсумовування.) У разі існування границі І функція f(x) називається інтегровною на про-
Вводячи поняття про визначений інтеграл як границю інтегральної суми й застосовуючи його позначення та формулу (5), рівність (4) можна переписати у вигляді:
Це відома формула Ньютона—Лейбніца, яка поєднує диференціальне числення з інтегральним. В інтегралі
Зауважимо, що означення визначеного інтеграла можна застосувати лише до обмеженої функції. Теорема 2.7. (Необхідна умова інтегрування.) Інтегровна на проміжку [a; b] функція обмежена. Властивості визначеного інтеграла Властивість 1.Визначений інтеграл є міра площі. Властивість 2. При переставленні меж інтегрування визначений інтеграл змінює знак, не змінюючи абсолютної величини. Наслідок. Властивість 3. (Поділ відрізка інтегрування.) Нехай точка c Î [а; b]. Тоді
Властивість 4. (Знак визначеного інтеграла.) 1. Якщо f(x) > 0 для х Î (а; b), a < b, то 2. Якщо f(x) < 0 для х Î (а, b), a < b, то Властивість 5.Якщо j(х) > y(х) для х Î (a; b), a < b, то справджується рівність: Властивість 6. Визначений інтеграл суми функцій подається як алгебраїчна сума інтегралів:
Властивість 7.Сталий множник можна виносити за знак визначеного інтеграла:
Властивість 8.Якщо функція f(x) інтегровна на [a; b] і а < b, то
Поиск по сайту: |
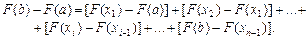 (2)
(2)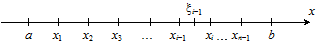
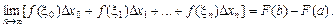 (4)
(4)
 називається визначеним інтеграломвід функції f(x) на відрізку
називається визначеним інтеграломвід функції f(x) на відрізку  (5)
(5)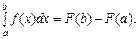 (6)
(6) символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо:
символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо: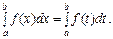
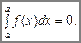
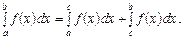 (10)
(10)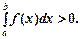

 (11)
(11)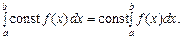 (12)
(12)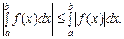 (13)
(13)