 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Частковий та повний прирости ф-ії двох змінних ⇐ ПредыдущаяСтр 4 из 4
Різницею Аналогічно визначаються прирости ф-ії більш ніж двох змінних.
Диференційовність ф-ії двох змінних Ф-ія
Головна лінійна структура приросту ф-ії, тобто АDх+ВDу називається повним диференціалом ф-ії (першим диференціалом) f(x;y) в точці x0, y0 і позначається dz:
Теорема: Якщо ф-ія z=f(x;y) диференційовна в точці (x0,y0), тоді існують границі:
Означення: Нехай ф-ія z=f(x;y) визначена в точці (х0;у0) і в її деякому околу. Якщо існує
Достатня умова диференційовності ф-ії двох змінних у точці Існування частинних похідних – необхідна, ала не достатня умова диференційовності ф-ії двох змінних в точці. Теорема: Якщо ф-ія z=f(x;y) в деякому околу точки (х0;у0) має неперервні частинні похідні, то вона диференційовна в точці (х0;у0).
Диференціювання складної ф-ії Теорема: Нехай на множині D визначена складна ф-ія z=f(u;v), де u=u(x;y), v=v(x;y) і нехай ф-ії u(x;y), v(x;y) мають у деякому околу точки (х0;у0)ÎD неперервні частинні похідні, а ф-ія z=f(u;v) має неперервні частинні похідні в деякому околу точки (u0;v0), де u0=u(x0;y0), v0=v(x0;y0). Тоді складна ф-ія z=f(u(x,y);v(x,y)) диференційовна в точці (х0;у0), причому
Похідна за напрямом. Градієнт Означення: Нехай ф-ія z=f(x;y) визначесна в деякому околі точки P0=(x0;y0); l деякий промінь з початком в точці P0=(x0;y0); P=(x;y) – точка на цьому промені, яка належить околу, що розглядається, – околу точки P0=(x0;y0); Dl – довжина відрізка P0Р. Границя В частинному випадку, Похідна за напрямом
Теорема: Якщо ф-ія z=f(x;y) має в точці P0=(x0;y0) неперервні частинні похідні, тоді в цій точці існує неперервна похідна
Означення: Вектор з координатами
Поиск по сайту: |
 називають повним приростом ф-ії
називають повним приростом ф-ії  при переході від точки (х0;у0) до точки
при переході від точки (х0;у0) до точки  і позначають Dz. Різницю
і позначають Dz. Різницю  називають Частковим приростом по х, а різницю
називають Частковим приростом по х, а різницю  - частковим приростом по у.
- частковим приростом по у. називається диференційовною у точці (х0;у0), якщо її повний приріст Dz можливо подати у вигляді:
називається диференційовною у точці (х0;у0), якщо її повний приріст Dz можливо подати у вигляді:  , де А, В – числа, a, b – нескінченно малі при Dxà0, Dyà0.
, де А, В – числа, a, b – нескінченно малі при Dxà0, Dyà0.

 , то вона називається частинною похідною по х (по у) функції в точці (х0;у0) і позначається
, то вона називається частинною похідною по х (по у) функції в точці (х0;у0) і позначається  або
або  .
.
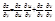
 , якщо вона існує, називається похідною ф-ії z=f(x;y) за напрямом
, якщо вона існує, називається похідною ф-ії z=f(x;y) за напрямом  в точці Р0 і позначається
в точці Р0 і позначається 
 – за напрямом осі Оу.
– за напрямом осі Оу. характеризує швидкість зміни ф-ії z=f(x;y) в точці P0=(x0;y0) за напрямом
характеризує швидкість зміни ф-ії z=f(x;y) в точці P0=(x0;y0) за напрямом  причому
причому 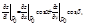 де
де  – значення частинний похідних в точці P0=(x0;y0).
– значення частинний похідних в точці P0=(x0;y0). , який характеризує напрям максимального зростання ф-ії z=f(x;y) в точці P0=(x0;y0)
, який характеризує напрям максимального зростання ф-ії z=f(x;y) в точці P0=(x0;y0)