 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МЕТОД ЗОНДОВЫХ ХАРАКТЕРИСТИК
Суть метода заключается в измерении тока заряженных частиц на помещённый в плазму металлический электрод малых размеров, на который накладывается задерживающий потенциал по отношению к аноду. Зависимость этого тока от потенциала электрода называется ЗОНДОВОЙ ХАРАКТЕРИСТИКОЙ. Из зондовой характеристики при определённых условиях можно вычислить концентрацию и температуру электронов плазмы, потенциал плазмы в том месте, где размещён зонд, функцию распределения электронов по энергиям. 1.3.1. ПОТЕНЦИАЛ ИЗОЛИРОВАННОГО ЗОНДА. Пусть мы имеем плоский, цилиндрический или сферический электрод (зонд), помещённый в плазму. Электроны и ионы, попадающие на поверхность изолированного зонда, заряжают его до определённого потенциала. Электроны вследствие малой массы имеют большую скорость, поэтому, если на зонд не подано напряжение, он заряжается отрицательно. Образующее поле будет отталкивать электроны и притягивать ионы, и, наконец, установится равновесие, при котором ток ионов Ii становится равным току электронов Ie. Такой, автоматически устанавливаемый потенциал изолированного зонда называется ПЛАВАЮЩИМ ПОТЕНЦИАЛОМ Uo. Таким образом, потенциал изолированного зонда Uo можно определить из условия: Ie = Ii Если же потенциал зонда изменить с помощью внешней цепи, то равновесие нарушается и на зонд потечёт ток: I = Ie – Ii 1.3.2. ЗОНДОВАЯ ХАРАКТЕРИСТИКА. Типичный ход зондовой характеристики представлен на рис.4. Ординаты кривой, направленные вниз, соответствуют току положительных ионов на зонд, ординаты, направленные вверх – току электронов из газа на зонд. Масштаб оси ординат для ветви кривой, лежащей ниже оси абсцисс, принят на рис.4 во много раз больший, чем для верхней ветви кривой. При сильно отрицательном зонде число падающих на него быстрых электронов исчезающе мало по сравнению с числом попадающих на зонд положительных ионов. Большому отрицательному потенциалу зонда соответствует левая часть характеристики, представляющая почти прямую линию АВ с небольшим наклоном. По мере уменьшения отрицательного потенциала зонда, на зонд начинают попадать в заметном количестве электроны. Электронный ток направлен противоположно ионному току и уменьшает общий ток на зонд. В точке К (рис.4) ток на зонд меняет своё направление при всё ещё отрицательном потенциале зонда по отношению к потенциалу плазмы.
1.3.3. СЛОЙ ПРОСТРАНСТВЕННОГО ЗАРЯДА. При отрицательном потенциале зонда по отношению к окружающему газу зонд окружён слоем положительного пространственного заряда, образованного положительными ионами, двигающимися к зонду. Этот слой экранирует потенциал зонда и способствует уменьшению ионного тока на него. В этом случае концентрацией электронов в слое можно пренебречь, вследствие чего при отсутствии столкновений его можно приближенно рассматривать как вакуумный диод, в котором эмиттером является поверхность квазинейтральной плазмы, а коллектором – поверхность зонда. Как известно, в вакуумном диоде с термокатодом при определённых условиях в промежутке между электродами может образоваться отрицательный объёмный заряд электронов. Из-за наличия этого заряда ток электронов, поступающих на анод, не зависит от эмиссионной способности катода и определяется только (при фиксированном межэлектродном расстоянии) разностью потенциалов U между электродами в степени "3/2". Для случая плоских электродов величина этого тока равна:
где S – площадь анода; е, mе - заряд и масса электрона; Uа – потенциал анода; d – межэлектродное расстояние. Распределение потенциала между электродами диода для этого случая изображено на рис.5,а. Штрихпунктирная линия представляет распределение потенциала в отсутствие объёмного заряда. Этот случай реализуется при достаточно больших потенциалах анода, когда плотность тока по формуле (1.10) превышает величину тока эмиссии катода (режим тока насыщения).
где S – площадь зонда; qi, mi – заряд и масса ионов; U – потенциал зонда относительно плазмы (здесь плазма – своего рода "эмиттер" электронов и ионов); d – толщина слоя пространственного заряда. Из (1.11) получаем:
Аналогичным образом для цилиндрического зонда радиусом rз можем написать:
где Для ионов значение F = 5,46×10–8×Mi-1/2, где Мi – атомный вес иона. Для цилиндрического зонда по найденным в эксперименте значениям b2 (где единицы измерения величин следующие: [rc] = [rз] =см, [U] =B, [L] = см, [Ii] = A) по таблице 1 можно определить величину эффективного радиуса слоя rс. Таблица 1
1.3.4. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАЗМЫ ПО ЭЛЕКТРОННОЙ ВЕТВИ ЗОНДОВОЙ ХАРАКТЕРИСТИКИ. Электроны плазмы проникают более или менее глубоко внутрь слоя у отрицательно заряженного зонда в зависимости от кинетической энергии каждого из них. При равновесном (максвелловском) распределении скоростей электронов концентрация nе электронов в любой точке тормозящего электроны поля по теореме Больцмана равна:
где noe – концентрация электронов в невозмущённой плазме; U(r) – потенциал (по абсолютной величине) этой точки по отношению к невозмущённой плазме; Te – температура электронов. Поток электронов n на зонд равен:
Учитывая (1.13) и (1.14) ток электронов на зонд будет равен:
где U = Uз –Un – разность потенциалов между зондом Uз и невозмущённой плазмой Un. Логарифмируя последнее выражение, получаем:
Следует заметить, что на участке CDEF зондовой характеристики (см. рис.4) вклад ионов невелик и почти весь ток электронный (ln½I½ » ln½Ie½). При более точных вычислениях необходимо экстраполировать ионный ток из области "насыщения" АВ зондовой характеристики в область более низких потенциалов зонда (см. рис.4) и в каждой точке участка CDEF вычислить величину чисто электронного тока Ie, a затем строить график зависимости ln½Iе½ = f(Uз). К сожалению, точный закон экстраполяции неизвестен, а линейная экстраполяция ионного тока не всегда даёт хорошие результаты. Поэтому можно и не учитывать ток ионов в первом приближении, либо пользоваться линейной экстраполяцией. Как видно из (1.16) тангенс угла наклона отрезка CD равен:
В точке G потенциал зонда Uз = Un и из (1.16) имеем:
Учитывая соотношение (1.13), можно определить величину noe:
Таким образом, этот метод даёт возможность: 1. Проверить по начальному ходу кривой lnIз = f(Uз) (где Iз – ток зонда), существует ли при данных условиях в плазме максвелловское распределение скоростей, и если это имеет место, т.е. если характеристика действительно имеет прямолинейный ход, то, далее 2. Найти значение потенциала в той точке пространства, в которой помещён зонд; 3. Найти температуру электронного тока в плазме Тe; 4. Найти плотность беспорядочного тока электронов в данной точке плазмы Ie; 5. Найти концентрацию электронов в плазме noе. Следует заметить, что существенным недостатком определения параметров плазмы по электронной ветви зондовой характеристики является возможность сильного перегрева зонда током насыщения и при определённых условиях даже переброса всего разряда с анода на зонд. По этим причинам определение параметров плазмы часто производят по ионной ветви зондовой характеристики.
1.3.5. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПЛАЗМЫ ПО ИОННОЙ ВЕТВИ. На участке АВС зондовой характеристики (см. рис.4) электронный ток сравним с ионным и здесь для определения Тe из электронной характеристики необходимо исключить ток ионов из полного тока на зонд. Однако, как уже упоминалось, сделать это очень сложно по причине значительных ошибок в определении этого тока методом экстраполяции. Поэтому для уменьшения влияния ионного тока на этом участке целесообразно воспользоваться методом первой производной зондового тока по потенциалу. Сущность метода состоит в том, что в области ВС электронный ток изменяется гораздо быстрее, чем ионный, т.е.
Следовательно, для определения температуры электронов имеет смысл строить график зависимости от потенциала зонда логарифма первой производной тока, а не самого тока. Можно показать, что в случае отрицательного отталкивающего потенциала зонда ток электронов на зонд равен:
Здесь noe – концентрация электронов в плазме; U – потенциал зонда относительно плазмы. Тогда, предполагая, что
из выражения (1.19) получаем:
Таким образом, наклон характеристики производной тока по напряжению в полулогарифмическом масштабе позволяет определить температуру электронов. Однако поскольку получение этой зависимости без применения специальных схем (типа устройств электрического дифференцирования) весьма затруднительно, то этот метод необходимо ещё более упростить. Воспользуемся тем, что при потенциале изолированного зонда Uз = Uo (т.е. в точке К рис.4) Ie = Ii. Тогда из выражения (1.19) с учётом условия (1.20) имеем:
Отсюда где dI/dU – тангенс угла наклона зондовой характеристики при потенциале изолированного зонда (Uз =Uo), Ii – ионный ток насыщения, экстраполированный по прямой линии к точке зондовой характеристики, где Uз = Uo. Поскольку
Итак, температуру электронов можно определить с помощью формулы (1.22) по ионной ветви зондовой характеристики. Концентрацию электронов также можно определить по участку АВ (рис.4). Для этого воспользуемся тем, что при достаточно большом отрицательном потенциале зонда электронным током на него можно пренебречь. Тогда на участке зондовой характеристики в районе точки А ток зонда I » Ii. Измерив ионный ток насыщения, теперь можно определить концентрацию ионов в невозмущённой плазме. Но для этого вначале необходимо определить радиус слоя объёмного заряда, иначе говоря, эффективную собирающую поверхность зонда Sэф. С этой целью в формулу (1.12) подставляют измеренную в опыте величину тока зонда I при большом отрицательном потенциале (при Uз = –60 В) и в качестве потенциала U – значение Uз – Uп, где Uз – потенциал зонда относительно анода, Uп – потенциал плазмы. Величину Uп обычно определяют по перегибу на электронной ветви зондовой характеристики (по точке К на рис.4). При отсутствии на характеристике электронной ветви по предложению Бома [1] можно принять, что
Таким образом,
где Uз = – 60В. Итак, из соотношения (1.12) путём вычислений по измеренным значениям тока зонда I (при потенциале Uз = –60В) и значению потенциала U по (1.2.3) находят величину
где l – длина зонда, rc – эффективный радиус зонда. Концентрацию ионов в плазме определяют по формуле Бома [1]:
где nio – концентрация ионов в невозмущённой плазме, Мi – молекулярный вес ионов. Поскольку в плазме nio = neo, то из формулы (1.25) можно получить расчётную формулу для определения концентрации электронов по ионной ветви:
где Ii – ионный ток при большом отрицательном потенциале зонда (Uз = -60В), Sэф – эффективная собирающая поверхность зонда. В формуле (1.26) единицы измерения [neo] = см–3, [Ii] = A, [Sэф] = см2, [Te] = °K, [Mi] = а.е.м. Следует заметить, что рассмотренная выше методика обработки зондовой характеристики применима только в условиях плазмы низкого давления, когда длины свободного пробега ионов и электронов больше, чем радиус эффективной поверхности зонда, т.е. движение частиц в слое пространственного заряда происходит без столкновений. При невыполнении этого условия обработка зондовой характеристики значительно усложняется.
Поиск по сайту: |
 Это происходит потому, что в газоразрядной плазме средняя кинетическая энергия электронов kTе во много раз больше средней кинетической энергии положительных ионов и электронный ток на отрицательно заряженный по отношению к газу зонд имеет заметную величину, перекрывающую ток положительных ионов. На участке ВКСД электронный ток увеличивается всё более и более. Участок ЕF соответствует насыщенному току электронов на зонд при потенциале зонда более высоком, чем потенциал окружающего зонд газа. Ток положительных ионов на зонд при этом режиме исчезающе мал. При дальнейшем увеличении потенциала зонда (точка F) возникает самостоятельный ток на зонд; из режима зонда он переходит в режим анода.
Это происходит потому, что в газоразрядной плазме средняя кинетическая энергия электронов kTе во много раз больше средней кинетической энергии положительных ионов и электронный ток на отрицательно заряженный по отношению к газу зонд имеет заметную величину, перекрывающую ток положительных ионов. На участке ВКСД электронный ток увеличивается всё более и более. Участок ЕF соответствует насыщенному току электронов на зонд при потенциале зонда более высоком, чем потенциал окружающего зонд газа. Ток положительных ионов на зонд при этом режиме исчезающе мал. При дальнейшем увеличении потенциала зонда (точка F) возникает самостоятельный ток на зонд; из режима зонда он переходит в режим анода. (1.10)
(1.10) Распределение потенциала в плазме вблизи зонда при наличии слоя пространственного заряда ионов изображено на рис.5,б. Как видно, на зонд могут попасть только ионы, энергия которых достаточна для преодоления положительного задерживающего потенциала Um. Плотность тока ионов на зонд можно определить по формуле, аналогичной (1.10) (далее все формулы в системе СГСЕ):
Распределение потенциала в плазме вблизи зонда при наличии слоя пространственного заряда ионов изображено на рис.5,б. Как видно, на зонд могут попасть только ионы, энергия которых достаточна для преодоления положительного задерживающего потенциала Um. Плотность тока ионов на зонд можно определить по формуле, аналогичной (1.10) (далее все формулы в системе СГСЕ): , (1.11)
, (1.11) , где
, где 
 , (1.12)
, (1.12) – табулированная функция отношения эффективного радиуса слоя rc к геометрическому радиусу зонда rз; L – длина зонда.
– табулированная функция отношения эффективного радиуса слоя rc к геометрическому радиусу зонда rз; L – длина зонда.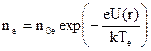 , (1.13)
, (1.13) (1.14)
(1.14) – средняя тепловая скорость электронов максвелловского распределения.
– средняя тепловая скорость электронов максвелловского распределения. , (1.15)
, (1.15) (1.16)
(1.16) Отсюда приходим к заключению, что логарифмическая характеристика электронного тока на зонд должна иметь вид, показанный на рис.6. Пока потенциал зонда Uз ниже, чем потенциал окружающей плазмы Un, эта характеристика представляет собой прямую линию CD (в соответствии с выражением (1.15)). Когда Uз делается равным потенциалу плазмы Un, в ходе характеристики lnIe = f(Uз) происходит изгиб и кривая быстро переходит в кривую насыщенного тока ЕF. Таким образом, по абсциссе точки изгиба кривой lnIе = f(Uз) можно определить потенциал невозмущённой плазмы Un.
Отсюда приходим к заключению, что логарифмическая характеристика электронного тока на зонд должна иметь вид, показанный на рис.6. Пока потенциал зонда Uз ниже, чем потенциал окружающей плазмы Un, эта характеристика представляет собой прямую линию CD (в соответствии с выражением (1.15)). Когда Uз делается равным потенциалу плазмы Un, в ходе характеристики lnIe = f(Uз) происходит изгиб и кривая быстро переходит в кривую насыщенного тока ЕF. Таким образом, по абсциссе точки изгиба кривой lnIе = f(Uз) можно определить потенциал невозмущённой плазмы Un. ; отсюда
; отсюда (1.17)
(1.17)
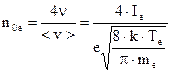 (1.18)
(1.18)
 (1.19)
(1.19)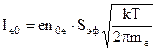 – величина тока электронов на зонд в отсутствие электрического поля (U = 0); Sэф – эффективная собирающая поверхность зонда;
– величина тока электронов на зонд в отсутствие электрического поля (U = 0); Sэф – эффективная собирающая поверхность зонда; (1.20)
(1.20)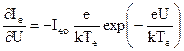 или
или  .
. (1.21)
(1.21) ,
,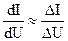 при
при  ® 0, то формулу (1.21) можно переписать в виде:
® 0, то формулу (1.21) можно переписать в виде: (1.22)
(1.22) ,
, , (1.2.3)
, (1.2.3) . Далее с помощью таблицы 1 определяют отношение rc/rз и вычисляют величину эффективной поверхности зонда:
. Далее с помощью таблицы 1 определяют отношение rc/rз и вычисляют величину эффективной поверхности зонда: , (1.24)
, (1.24) , (1.25)
, (1.25)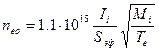 , (1.26)
, (1.26)