 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
РЕПРЕЗЕНТАТИВНОСТЬ ТЕСТОВЫХ НОРМСтр 1 из 2Следующая ⇒
Основные статистические принципы построения тестов достаточно полно освещены в появившейся в начале 80-х годов на русском языке литературе по дифференциальной психометрике (Аванесов В. С., 1982; Анастази А., 1982; Гайда В. К., Захаров В. П., 1982). Тем не менее в указанных руководствах центральная проблема психометрики тестов - вопрос о тестовых нормах - еще не получила последовательного освещения. Прежде всего это относится к руководству известной представительницы американской тестологии А. Анастази. В руководстве Анастази не получают достаточного критического обсуждения две основополагающие предпосылки традиционной западной тестологии: вопрос о применении статистических норм (квантилей распределения баллов) в качестве диагностических норм и вопрос о сведении всех эмпирических распределений к нормальной модели. Ниже эти предпосылки будут проанализированы в контексте краткой реконструкции системы основных понятий дифференциальной психометрики. Статистическая природа тестовых шкал. Типичный измерительный тест в психодиагностике - это последовательность кратких заданий, или пунктов, дающая в результате ее выполнения испытуемым последовательность исходов, которая затем подвергается однозначной количественной интерпретации. Примеры интерпретации в интеллектуальных тестах, состоящих из отдельных задач: «правильное решение», «ошибочное решение», «отсутствие ответа» (пропуск задачи из-за нехватки времени). Примеры интерпретации в случае личностных опросников, состоящих из высказываний, предлагаемых для подтверждения испытуемым: «подтверждение» (ответ «верно»), «отвержение» (ответы «не согласен», «неверно»). Суммарный балл по тесту подсчитывается с помощью ключа: ключ устанавливает числовое значение исхода по каждому пункту. Например, за правильное решение задания дается «+1», за неправильное решение или пропуск - «О». Тогда балл буквально выражает количество правильных ответов. Исход по отдельному заданию подвержен воздействию не только со стороны измеряемого фактора - способности или черты личности испытуемого, но и побочных шумовых факторов, которые являются иррелевантными по отношению к задаче измерения. Примеры случайных факторов: колебания внимания, вызванные неожиданными отвлекающими событиями (шум на улице, стук в дверь и т. п.), трудности в понимании смысла задания (вопроса), вызванные особенностями опыта данного конкретного испытуемого, и т. п. Последовательность исходов оказывается последовательностью событий, содержащей постоянный и случайный компоненты. Как известно, основным приемом, позволяющим устранить искажающее влияние случайных факторов на результат (суммарный балл), Является балансировка этого влияния с помощью повторения. При этом фактически предполагается, что повторение обеспечивает рандомизацию (случайное варьирование) неконтролируемого фактора, в результате чего при суммировании исходов Положительные и негативные эффекты случайных факторов взаимопоглощаются (о механизме рандомизации см.: Готтсданкер Р., 1982). В оптимальном тесте набор и последовательность заданий организуются таким образом, чтобы повысить долю постоянного компонента и сократить долю случайного в величине суммарного балла. Тем не менее, несмотря на различные статистические ухищрения, суммарный балл в психологических измерениях содержит несравненно большую долю случайного компонента, чем в обычных физических измерениях. В силу этого суммарный балл оказывается определенным лишь в известных пределах, заданных ошибкой измерения. Для того чтобы оценить эффективность, дифференциальную ценность всей процедуры измерения, необходимо соотнести размеры ошибки измерения с размерами разброса суммарных баллов, вызванных индивидуальными различиями в измеряемой характеристике между испытуемыми. В терминах Статистики речь идет о сравнении так называемой истинной дисперсии распределения суммарных баллов с дисперсией ошибки. Именно этим обусловлен необходимый интерес психометристов к распределению суммарных баллов. Поэтому анализ распределения необходим не только при использовании статистических норм, но и в случае абсолютных и критериальных норм. Как известно, частотное распределение суммарных баллов имеет удобную графическую интерпретацию в виде кривых распределений: гистограммы и кумуляты (см., в частности, удачное популярное введение в описание распределений в книге: Кимбл Г., 1982, с. 55-70). В случае гистограммы по оси абсцисс откладываются «сырые очки» -первичные показатели суммарных баллов, возможных для данного теста, по оси ординат - относительные частоты (или проценты) встречаемости баллов в выборке стандартизации (Анастази А., 1982, с. 66). Как известно, для «колоколообразной» кривой нормального распределения дисперсия визуализируется как параметр, ответственный за «распластанность» графика плотности вероятности (теоретического аналога эмпирической кумуляты) вдоль оси X. Чтобы визуализировать дисперсию ошибки измерения, нужно было бы многократно провести тест с одним испытуемым и построить графическое распределение частот его индивидуальных баллов (рис. 1). Очевидно, что дифференцирующая способность теста сводится к нулю, если кривые, иллюстрирующие «истинную» и «ошибочную» дисперсии» совпадают. Как видим, анализ распределения тестовых баллов необходим уже для анализа надежности теста (см. раздел 3.2). Проблема меры в психометрике и свойства пунктов теста. В физических измерениях калибровка шкалы производится на основе контроля за равномерным варьированием измеряемого свойства в эталонных объектах. Носителем меры является эталон- физический объект, стабильно сохраняющий заданную величину измеряемого свойства. В дифференциальной психометрике такие физические эталоны отсутствуют: мы не располагаем индивидами, которые были бы постоянными носителями заданной величины измеряемого свойства.
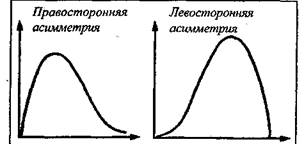
Рис. 1.Соотношение индивидуальной и общей вариации тестовых баллов Роль косвенных эталонов в психометрике выполняют сами тесты: в том смысле, в каком трудность задач можно рассматривать как величину, прямо пропорционально сопряженную со способностью (чем труднее задача, тем выше должен быть уровень способности, требуемый для ее решения). Аналогом понятия «трудность» для «ли-вопросов»[1] опросника является «сила»: более «сильные» высказывания (в логическом смысле) вызывают подтверждение (согласие) у меньшего числа испытуемых. Ни трудность, ни силу пунктов теста нельзя выявить иначе, чем с помощью проведения теста. Операциональным определением трудности оказывается «процентильная мера»: процент испытуемых, справившихся с заданием теста (или ответивших «верно» на «ли-вопрос»). Чем меньше процент, тем выше трудность. Кривая распределения тестовых баллов отражает свойства пунктов, из которых составлен тест. Если кривая имеет правостороннюю асимметрию, то в тесте преобладают трудные задания; если кривая имеет левостороннюю асимметрию, значит, большинство пунктов в тесте - легкие (слабые) (рис. 2).
Рис. 2.Асимметрии распределения тестовых баллов Тесты первого типа плохо дифференцируют испытуемых с низким уровнем способностей: все эти испытуемые получают примерно одинаковый низкий балл. Тесты второго типа, наоборот, хуже дифференцируют испытуемых с высоким уровнем способностей. Если пункты обладают оптимальным уровнем трудности (силы), то кривая распределения зависит от того, насколько пункты однородны. Если пункты разнородны (исход по одному пункту не предопределяет исход по другому), то мы получаем тест в виде последовательности независимых испытаний Бернулли. Как известно из математической статистики, при достаточно большом количестве независимых испытаний с двумя разновероятными исходами кривая биномиального распределения (кривая суммарного балла) по закону больших чисел автоматически приближается к кривой нормального распределения (центральная предельная теорема Муавра - Лапласа). Если тест содержит разнородные задания примерно равного уровня трудности (именно такие задания и подбираются для измерения интегральных свойств личности), то нормальность распределения суммарных баллов возникает автоматически - как артефакт самой процедуры подсчета суммарных баллов. При этом, конечно, форма кривой распределения баллов не позволяет говорить о реальной форме распределения измеряемого свойства, каким оно является само по себе - в широкой популяции испытуемых. Нормальность распределения есть артефакт, прямое следствие направленного отбора пунктов с заданными свойствами. Если подбираются пункты, тесно положительно коррелирующие между собой (испытания не являются статистически независимыми), то в распределении баллов возникает отрицательный эксцесс (рис. 3,а), Максимальных значений отрицательный эксцесс достигает по мере возрастания вогнутости вершины распределения - до образования двух вершин -двух мод (с «провалом» между ними -рис. 3,6). Бимодальная конфигурация распределения баллов указывает на то, что выборка испытуемых разделилась на две категории (с плавными переходами между ними): одни справились с большинством заданий (согласились с большинством «ли-вопросов»), другие - не справились.
Рис. 3. Отрицательные (а, б) положительный (в) эксцессы распределения тестовых баллов
Такая конфигурация распределения свидетельствует о том, что в основе пунктов лежит какой-то один общий им всем признак, соответствующий определенному свойству испытуемых: если у испытуемых есть это свойство (способность, умение, знание), то они справляются с большинством пунктов, если этого свойства нет - то не справляются. В некоторых редких ситуациях пункты могут отрицательно коррелировать друг с другом. В этом случае на кривой возникает положительный эксцесс (рис. 3, в): вся масса эмпирических точек собирается вблизи среднего значения. Такое возможно в двух случаях: 1) когда ключ составлен неверно -объединены при подсчете отрицательно связанные признаки, которые обусловливают взаимоуничтожение баллов; 2) когда испытуемые применяют, разгадав направленность опросника, специальную тактику «медианного балла» - искусственно балансируют ответы «за» и «против» одного из полюсов измеряемого качества. Итак, когда в качестве единственного эталона измерения психодиагностами рассматривается сам тест, то в качестве меры измеряемого свойства выступает положение балла на кривой распределения. Применяется процентильная шкала. В качестве универсальной меры, пригодной для разных (по своей качественной направленности и количеству пунктов) тестов, используется «процентильная мера». Процентилъ — процент испытуемых из выборки стандартизации, которые получили равный или более низкий балл, чем балл данного испытуемого. Таким образом, в качестве источника данной меры выступает нормативная выборка (выборка стандартизации), на которой построено нормативное распределение тестовых баллов. Процентильные шкалы лежат в основе всех традиционных шкал, применяемых в тестологии (Т-очки MMPI, баллы IQ, стены 16 PF и др.). Подчеркнем, что с точки зрения теории измерений, процентильные шкалы относятся к порядковым шкалам: они дают информацию о том, у кого из испытуемых сильнее выражено измеряемое свойство, но не позволяют говорить о том, во сколько раз сильнее. Для того чтобы строить на базе таких шкал количественный прогноз, нужно повысить уровень измерения (популярное изложение представлений о теории измерений см. в книге: Клигер С. А. и др., 1978). Переход к шкалам интервалов производят либо на базе эмпирического распределения, либо на базе произвольной модели теоретического распределения. В абсолютном большинстве случаев в роли такой теоретической модели оказывается модель нормального распределения (хотя в принципе может быть использована любая модель). В целом кроме статистических, процентильных шкал следует отличать нередко используемые в дифференциальной психометрике еще 2 вида шкал (и соответственно 2 вида тестовых норм). Это, во-первых, то, что можно условно назвать «абсолютными тестовыми нормами» — в роли шкалы для вынесения диагноза выступает сама шкала «сырых» очков, во-вторых, «критериальные» тестовые нормы. Применение таких норм можно считать оправданным в двух случаях: 1) когда сама тестовая «сырая» шкала имеет практический смысл (например, студент, изучающий иностранный язык, должен знать как можно больше слов этого языка, и сырой показатель лексического теста имеет практический смысл); 2) когда сырой балл по тесту в результате эмпирических исследований связывается с заданной вероятностью успешности какой-либо практической деятельности (вероятность успеха «критериальной» деятельности, каковой для упомянутого выше примера может быть синхронный перевод монолога в течение 30 минут). Процентильная нормализация шкалы. Выше Показано, что нормальность распределения достигается искусственным подбором пунктов теста с заданными статистическими свойствами: Опишем еще ряд процедур, которые также широко используются для искусственной нормализации. 1. Нормализация пунктов. Ключ для данного пункта корректируется на базе нормальной модели. Если среди нормативной выборки с данным заданием справились только 16 % испытуемых, то данному пункту на интервальной шкале «трудности» (при условии априорного принятия нормальной модели с параметрами М = 0 и а = 1) соответствует значение +1 (см. график в книге: Анастазй А., 1982, с. 181). Если справились 75 % испытуемых, то балл пункта на сигма-шкале равен-0,67. В результате суммирования по пунктам баллов, скорректированных нормализацией, суммарные баллы лучше приближаются к нормальному распределению. 2. Нормализация распределения суммарных баллов (или интервальная нормализация). В этом случае по таблице нормального распределения (нормального интеграла) производится переход от процентильной шкалы к сигма-шкале: используется функция, обратная интегральной, - от ординаты производится переход к абсциссе нормального распределения.
Рис. 4. Преобразование процентильной шкалы (по оси X) в нормализованную сигма-шкалу (по оси Y)
На рис. 4 дана условная графическая иллюстрация этого перехода (кривая, обратная традиционной S-образной интегральной кривой нормального распределения). Приведем пример интервальной нормализации (табл. 3). Пусть строка X содержит сырые баллы (не нормализованные) по тесту, полученные простым подсчетом правильных ответов. В строке Р - частоты встречаемости сырых баллов в выборке из 62 испытуемых. В строке F - кумулятивные частоты: Таблица 3
Трудность, с которой сталкиваются начинающие при использовании интервальной нормализации, состоит в том, что обычные статистические таблицы не приспособлены для психометрики: нужно отыскивать значение процентильного ранга внутри таблицы, а соответствующую сигма-оценку – с краю. Для облегчения ориентации приведем фрагмент таблицы соответствий PR, а и стенов (табл. 4): Таблица 4
В обычных таблицах из соображений симметрии даны лишь значения для PR > 50. Для PR < 50 соответствующие значения находятся из тех же таблиц σ = ψ -1(1- PR/100). Например, для PR =35 мы находим 1 - PR/100 = 1 - 0,35 = 0,65, затем - по табл. ψ -1 = 0,39 и берем это значение с отрицательным знаком -0,39. Для нормализации удобно пользоваться графическим методом (нормальной бумагой, стандартной 5-образной кривой и т. п.). В результате нормализации интервалы между исходными сырыми баллами переоцениваются в соответствии с нормальной моделью. В отличие от процентильной шкалы, нормальная шкала придает больший вес (в дифференциации испытуемых) краям распределения: различия между испытуемыми, набравшими 95 и 90 процентилей, оцениваются как более высокие, чем различия между испытуемыми, набравшими 65 и 60 процентилей. В применении к шкалам оценок (рейтинговым шкалам) метод нормализации интервалов называется «методом последовательных интервалов» (Клигер С. А. и др., 1978, с. 75-81). В результате применения процедуры нормализации исследователь-психометрист получает для нормативной выборки таблицу перевода сырых баллов в нормализованные баллы. На основе этих таблиц часто строят графики: деления сырых баллов наносят на числовую ось с неравными интервалами, так что эмпирическое распределение частот максимально близко приближается к нормальной форме. Пример такой графической нормализации - профильные листы MMPI (Анастази А., 1982, с. 129). Так как нормальное распределение описывается всего двумя параметрами: средним М (мерой положения) и средним квадратическим (или стандартным) отклонением а (мерой рассеяния), то диагностические нормы в случае нормализованных шкал описываются в единицах отклонений от среднего по выборке; например, заключают, что испытуемый А показал результат, превышающий средний балл на две сигмы, испытуемый В -результат, оказавшийся ниже среднего балла на одну сигму, и т. п. На процентильной шкале этому соответствуют процентильные ранги 95 и 16 соответственно. Переход к нормальному распределению создает очень удобные условия для количественных операций с диагностической шкалой: как со шкалой интервалов с ней можно производить операции линейного преобразования (умножение и сложение), можно описывать диагностические нормы в компактной форме (в единицах отклонений), можно применять линейный коэффициент корреляции Пирсона, критерии для проверки статистических гипотез, построенные в применении к нормальному распределению, т. е. весь аппарат традиционной статистики (основанной на нормальном распределении). ! Неправомерность онтологизации нормального закона. В традиционной психометрике нормальное распределение выступает в роли инструментального понятия, облегчающего оперирование с данными. Но это не означает, что можно забывать об искусственном происхождении нормального распределения. Традиции западной тестологии, основанные еще Ф. Гальтоном, предполагают однородность теоретических представлений психометрики и биометрики. Точно так же как происхождение нормального распределения при исследовании вариативности биологических характеристик человеческого организма связывается с наличием взаимодействия постоянного фактора генотипа и изменчивых случайных факторов фенотипа, - происхождение межиндивидуальных психологических различий связывается с генетическим кодом, якобы предопределяющим положение индивида на оси нормальной кривой. В действительности же нет никаких оснований приписывать появление нормальной кривой, часто получаемой с помощью специальных статистических непростых процедур, действию механизма наследственности. В тех случаях, когда на большой выборке удается получить нормальное распределение без каких-либо искусственных способствующих этому мер, это опять-таки не означает вмешательства генетики. Закон нормального распределения воспроизводится всякий раз, когда на измеряемое свойство (на формирование определенного уровня способностей индивида) действует множество разных по силе и направленности факторов, независимых друг от друга. История прижизненных средовых воздействий, которые испытывает на себе субъект, также подобна последовательности независимых событий: одни факторы действуют в благоприятном направлении, другие - в неблагоприятном, а в результате взаимопогащение их влияний происходит чаще, чем тенденциозное однонаправленное сочетание (большинство благоприятных или большинство неблагоприятных), т. е. возникает нормальное распределение. Массовые исследования показывают, что введение контроля над одним из средовых популяционных факторов (уровень образования родителей, например) приводит к расслоению кривой нормального распределения: выборочные кривые оказываются смещенными относительно друг друга (Анастази А., 1982, с. 201). Эти результаты служат ярким подтверждением социокультурного происхождения статистических диагностических норм, что одновременно служит основанием для серьезных предосторожностей при переносе норм, полученных на одной популяции, на другие популяции. Однородными можно считать только те популяции, по отношению к которым действует одинаковый механизм выборки: ив ситуации создания (стандартизации) теста, и в ситуации его диагностического применения. Здесь приходится учитывать и такие нюансы выборочного механизма, как феномен нормальных добровольцев. Если выборку стандартизации формировать на студентах, добровольно согласившихся участвовать в тестировании, а применение теста планируется на сплошных выборках (в административном порядке), то это грозит определенными ошибками в диагностических суждениях, так как психологический портрет «добровольца» в существенных чертах отличается от портрета испытуемого, соглашающегося на тестирование только под административным давлением (Шихирев П.Н, 1979, с. 181). Подсчет параметров и оценка типа распределения. Для описания выборочного распределения, как правило, используются следующие известные параметры:
1. Среднее арифметическое значение:
где xj – балл i-го испытуемого; yi -значение i-го балла по порядку возрастания; pi - частота встречающегося i-го балла; n - количество испытуемых в выборке (объем); m - количество градаций шкалы (количество баллов).
1. Среднее квадратическое (стандартное) отклонение: 2.
где 3. Асимметрия:
где S - стандартное отклонение; θ - среднее кубическое значение: С - среднее квадратическое: 4. Эксцесс:
где Q - среднее значение четвертой степени: Стандартная ошибка среднего арифметического значения (математического ожидания) оценивается по формуле:
На основе ошибки математического ожидания строятся доверительные интервалы: Если тестовый балл какого-либо испытуемого попадает в границы доверительного интервала, то нельзя считать, что испытуемый обладает повышенным (или пониженным) значением измеряемого свойства с заданным уровнем статистической значимости. Асимметрия и эксцесс нормального распределения должны быть равны нулю. Если хотя бы один из двух параметров существенно отличается от нуля, то это означает анормальность полученного эмпирического распределения. Проверку значимости асимметрии можно произвести на основе общего неравенства Чебышева:
где Sa - дисперсия эмпирической оценки асимметрии:
где р - уровень значимости или вероятность ошибки первого рода: ошибки в том, что будет принят вывод о незначимости асимметрии при наличии значимой асимметрии (в формулу подставляют стандартные р = 0,05 или р = 0,01 и проверяют выполнение неравенства). Сходным образом оценивается значимость эксцесса:
где Sе - эмпирическая дисперсия оценки эксцесса:
] Гипотезы об отсутствии асимметрии и эксцесса принимаются с вероятностью ошибки р (пренебрежимо малой), если выполняются неравенства (3.1.6) и (3.1.8). Более легкий метод проверки нормальности эмпирического распределения основывается на универсальном критерии Колмогорова. Для каждого тестового балла у. (для каждого интервала равнозначности при дискретизации непрерывной хронометрической шкалы) вычисляется величина D. - модуль отклонения эмпирической и теоретической интегральных функций распределения:
где F- эмпирическая интегральная функция (значение кумуляты в данной точке уj); U — теоретическая интегральная функция, взятая из таблиц[2]. Среди Dj отыскивается максимальное значение Dmax В таблице 5 приведены асимптотические критические значения для распределения Колмогорова (при Таблица 5
Если проверка согласованности эмпирического распределения с нормальным дает положительные результаты, то это означает, что полученное распределение можно рассматривать как устойчивое -репрезентативное по отношению к генеральной совокупности - и, следовательно, на его основе можно определить репрезентативные тестовые нормы. Если проверка не выявляет нормальности на требуемом уровне, то это означает, что либо выборка мала и нерепрезентативна к популяции, либо измеряемые свойство и устройство теста (способ подсчета) вообще не дают нормального распределения. В принципе отнюдь не обязательно все нормативные распределения сводить к нормальным. Можно с равным успехом пользоваться хорошо разработанными моделями гамма-распределения, пуассоновского распределения и т. п. Критерий Колмогорова позволяет оценить близость вашего эмпирического распределения к любому теоретическому распределению. При этом устойчивым и репрезентативным может оказаться распределение любого типа. Если из нормальности, как правило, следует устойчивость, то обратное неверно -устойчивость вовсе не обязательно предполагает нормальность распределения. Наличие значимой положительной асимметрии (см. рис. 2,а) свидетельствует о том, что в системе факторов, детерминирующих значение измеряемого показателя, преобладают факторы, действующие в одном направлении - в сторону повышения показателя. Такого рода отклонения появляются при использовании хронометрических показателей: испытуемый не может решить задачу быстрее определенного минимально необходимого периода, но может существенно долго задерживаться с ее решением. На практике распределения такого рода преобразуют в приближенно нормальное распределение с помощью логарифмической трансформации:
При этом говорят, что распределение хронометрических показателей подчиняется «логнормальному» закону. Подобную алгебраическую нормализацию тестовой шкалы применяют и к показателям с еще более резко выраженной положительной асимметрией. Например, в процедурах контент-анализа сам тестовый показатель является частотным: он измеряет частоту появления определенных категорий событий в текстах. Для редких категорий вероятность появления значительно меньше 0,5. Формула преобразования
позволяет придать необходимую 5-образную форму кумуляте. Стандартизация шкалы. В психометрике следует различать две формы стандартизации. Под стандартизацией теста понимают прежде всего стандартизацию самой процедуры проведения инструкций, бланков, способа регистрации, условий и т. п. Без стандартизации теста невозможно получить нормативное распределение тестовых баллов и, следовательно, тестовых норм. Под стандартизацией шкалы понимают линейное преобразование масштаба нормальной (или искусственно нормализованной) шкалы. В общем случае формула стандартизации выглядит так:
где xi - исходный балл по «сырой» шкале, для которой доказана нормальность распределения;
М- математическое ожидание по выбранной стандартной шкале; σ - стандартное отклонение по стандартной шкале. Если шкала подвергалась предварительной искусственной нормализации интервалов, то формула упрощается: zj =σ zj =M (3.1.14)
Приведем параметры для наиболее популярных стандартных шкал: 1) T -шкала Маккола (тест-опросник MMPI и другие тесты): М = 50 и σ = 10, 2) шкала IQ : М = 100 и σ = 15, 3) шкала «стэнайнов» (целые численные значения от 1 до 9 -стандартная девятка): М = 5,0 и σ = 2, 4) шкала «стенов» (стандартная десятка, 16PF Кеттелла): М = 5,5 .и σ = 2. Чтобы различать стандартные баллы, полученные с помощью линейной стандартизации и нелинейной нормализации интервалов, Р. Кеттелл ввел понятие «S-стенов» и «n-стенов». Таблицы «и-стенов», естественно, точнее отражают квантили эмпирического нормального распределения. Приведем образец такой таблицы для фактора А из тест-опросника 16PF;
Сырые баллы 0-4 5-6 7 8-9 10-12 13 14-15 16 17-18 19-20 Стены 1 2 3 4 5 6 7 8 9 10
Применение стандартных шкал позволяет использовать более грубые, приближенные способы проверки типа распределения тестовых баллов. Если, например, процентильная нормализация с переводом в стены и линейная нормализация с переводом в стены по формуле (3.1.13) дают совпадающие целые значения стенов для каждого Y, то это означает, что распределение обладает нормальностью с точностью до «стандартной десятки». Применение стандартных шкал необходимо для соотнесения результатов по разным тестам, для построения «диагностических профилей» по батарее тестов и тому подобных целей. Проверка устойчивости распределения. Общая логика проверки устойчивости распределения основывается на индуктивном рассуждении: если половинное (полученное по половине выборки) распределение хорошо моделирует конфигурацию целого распределения, то можно предположить, что это целое распределение будет также хорошо моделировать распределение генеральной совокупности. Таким образом, доказательство устойчивости распределения означает доказательство репрезентативности тестовых норм. Традиционный способ доказательства устойчивости сводится к наличию хорошего приближения эмпирического распределения к какому-либо теоретическому. Но если эмпирическое распределение не приближается к теоретическому, несмотря на значительное увеличение объема выборки, то приходится прибегать к более общему индуктивному методу доказательства. Простейший его вариант может быть сведен к получению таблиц перевода сырых баллов в нормализованную шкалу по данным всей выборки и применению этих таблиц для каждого испытуемого из половины выборки; если распределение нормализованных баллов из половины выборки хорошо приближается к нормальному, то это значит, что заданные таблицами нормализации тестовые нормы определены устойчиво. Близость к нормальному распределению проверяется с помощью критерия Колмогорова (при n <200 целесообразно использовать более мощные критерии: «хи-вадрат» или «омега-квадрат»). При этом под «половиной выборки» подразумевается случайная половина, в которую испытуемые зачисляются случайным образом -с помощью двоичной случайной последовательности (типа подбрасывания монетки и т. п.). В более общем случае такой простейший метод установления однородности двух эмпирических распределений может быть применен и при разбиении выборки по какому-либо систематическому признаку. Если, в частности, по какому-либо из популяционно значимых признаков (пол, возраст, образование, профессия) психолог получает значимую неоднородность эмпирических распределений; то это значит, что относительно данных популяционных категорий тестовые нормы должны быть специализированы (одна таблица норм - для мужчин, другая - для женщин и т. д.). Более статистически корректный метод проверки однородности двух распределений, полученных при расщеплении выборки на равные части, опять же связан с применением критерия Колмогорова. Для этого с табличным значением сравнивается:
где Ке - эмпирическое значение статистики Колмогорова; Fj1 - кумулятивная относительная частота для у-того интервала шкалы по первой половине выборки; Fj2 - та же частота для второй половины; n - полный объем выборки. Точные значения квантилей распределения Колмогорова для определения размеров выборки можно найти в кн.: Мюллер П. и др., 1982. Применение критерия Колмогорова не зависит от нормальности целого распределения и от необходимости производить нормализацию интервалов. * * *
Итак, априорная предпосылка нормальности распределения тестовых баллов основывается скорее на принципах операционального удобства, чем на теоретической необходимости. Психометрически корректные процедуры получения устойчивых тестовых норм возможны с помощью специальных методов непараметрической статистики (критерий «хи-квадрат» и т. п.) для распределений произвольной формы. Выбор статистической модели распределения - законный произвол психометриста, пока сам тест выступает в качестве единственного эталона измеряемого свойства. В этом случае остается лишь тщательно следить за соответствием сферы применения диагностических норм той выборке испытуемых, на которой они были получены. Произвольность в выборе статистической модели шкалы исчезает, когда речь заходит о внешних по отношению к тесту критериях. Репрезентативность критериальных тестов. В таких тестах в качестве реального эталона применяется критерий, ради которого создается тест, - целевой критерий. Особое значение такой подход имеет в тех областях практики, где высокие результаты могут дать узкоспециализированные диагностические методики, нацеленные на очень конкретные и узкие критерии. Такая ситуация имеет место в обучении: тестирование, направленное на получение информации об уровне усвоения определенных знаний, умений и навыков (При профессиональном обучений), должно точно отражать уровень освоения этих навыков и тем самым давать надежный прогноз эффективности конкретной профессиональной деятельности, требующей применения этих навыков. Так возникают «тесты достижений», по отношению к которым критериальный подход обнаружил свою высокую эффективность (Гуревич К. М, Лубовский В. И,, 1982). Рассмотрим операциональную схему шкалирования, применяемую при создании критериального теста. Пусть имеется некоторый критерий С, ради прогнозирования которого психодиагност создает тест X. Для простоты представим С как дихотомическую переменную с двумя значениями: 1 и 0. С, = 1 означает, что j-й субъект достиг критерия (попал в «высокую» группу по критерию), Сj=0 означает, что i-й субъект не достиг критерия (попал в «низкую» группу). Психодиагност применяет на нормативной выборке тест X, и в результате каждый индивид получает тестовый балл Xi. После того как для каждого индивида из выборки становится известным значение С (иногда на это требуются месяцы и годы после момента тестирования), психодиагност группирует индивидов по порядку возрастания балла Xi и для каждого деления исходной шкалы сырых тестовых баллов подсчитывает эмпирическую вероятность Р попадания в «высокую» группу по критерию С. На рис. 5 показаны распределения вероятности Р (Ci = 1) в зависимости от Xi
Рис. 5 Эмпирическая зависимость между вероятностью критериального события и тестовым баллом
Очевидно, что кривая на рис. 5 по своей конфигурации может совершенно не совпадать с кумулятивной кривой распределения частот появления различных Xi. Кривая, представленная на рис. 5, является эмпирической линией регрессии С по Xi Теперь можно сформулировать основное требование к критериальному тесту: линия регрессии должна быть монотонной функцией С от Xi Иными словами, ни для одного более высокого значения X. вероятность Р не должна быть меньшей, чем для какого-либо менее высокого значения Xi Если это условие выполняется, то открывается возможность для критериального шкалирования сырых баллов X. Так же как в случае с интервальной нормализацией», когда применяется поточечный перевод интервалов Х в интервалы Z, для которых выполняется нормальная модель распределения, так и при критериальном шкалировании к делениям сырой шкалы X применяется поточечный перевод прямо в шкалу Р на основании эмпирической линии регрессии. Например, если испытуемый А получил по тесту X 18 сырых баллов и этому результату соответствует Р=0,6, то испытуемому А ставится в соответствие показатель 60 %. Конечно, любая эмпирическая кривая является лишь приближенной моделью той зависимости, которая могла бы быть воспроизведена на генеральной совокупности. Обычно предполагается, что на генеральной совокупности линия регрессии С по Х должна иметь более сглаженную форму. Поэтому обычно предпринимаются попытки аппроксимировать эмпирическую линию регрессии какой-либо функциональной зависимостью, что позволяет затем производить прогноз с применением формулы (а не таблицы или графика). Например, если линия регрессии имеет вид приблизительно такой, какой изображен на рис. 6, то применение процентильной нормализации позволяет получить простую линейную регрессию С по нормализованной шкале Z. Это как раз тот случай, когда имеет место эквивалентность стратегии, использующей выборочно-статистические тестовые нормы, и стратегии, использующей критериальные нормы.
Рис. 6. Зависимость вероятности критериального события Р от
Поиск по сайту: |



 =
=  . В строке F* - кумулятивные баллы:
. В строке F* - кумулятивные баллы: 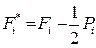 . В строке PR - процентильные ранги:
. В строке PR - процентильные ранги:  . В строке σ даются нормализованные баллы, полученные из соответствующих процентильных рангов по таблицам, а -оценки часто называются в зарубежной литературе также z-оценками.
. В строке σ даются нормализованные баллы, полученные из соответствующих процентильных рангов по таблицам, а -оценки часто называются в зарубежной литературе также z-оценками. , (3.1.1)
, (3.1.1)
 , (3.1.2)
, (3.1.2) - сумма квадратов тестовых баллов для и испытуемых.
- сумма квадратов тестовых баллов для и испытуемых. (3.1.3)
(3.1.3) - среднее арифметическое значение;
- среднее арифметическое значение; ,
,
 , (3.1.4)
, (3.1.4) .
. (3.1.5)
(3.1.5) )
) (3.1.6)
(3.1.6) , (3.1.7)
, (3.1.7)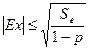 (3.1.8)
(3.1.8) . (3.1.9)
. (3.1.9) (3.1.10)
(3.1.10) , и величина
, и величина  сравнивается с табличным значением
сравнивается с табличным значением  критерия Колмогорова.
критерия Колмогорова. ). Близость эмпирического значения λе к левосторонним стандартным квантилям λt позволяет констатировать близость эмпирического и предполагаемого теоретического распределения с пренебрежимо малой вероятностью ошибки р (0,01; 0,05; 0,10 и т, п.). Близость λе к правосторонним стандартным квантилям λt позволяет сделать вывод о статистически значимом отсутствии согласованности эмпирического и теоретического распределений. Надо помнить, что критерий Колмогорова, очень простой в вычислительном' отношении, обеспечивает надежные выводы лишь при
). Близость эмпирического значения λе к левосторонним стандартным квантилям λt позволяет констатировать близость эмпирического и предполагаемого теоретического распределения с пренебрежимо малой вероятностью ошибки р (0,01; 0,05; 0,10 и т, п.). Близость λе к правосторонним стандартным квантилям λt позволяет сделать вывод о статистически значимом отсутствии согласованности эмпирического и теоретического распределений. Надо помнить, что критерий Колмогорова, очень простой в вычислительном' отношении, обеспечивает надежные выводы лишь при  200: Критерий Колмогорова резко снижает свою эффективность, когда наблюдения группируются по малому количеству интервалов равнозначности. Например, при n = 200 количество интервалов должно быть не менее 20 (примерно по 10 наблюдений на каждый интервал в среднем).
200: Критерий Колмогорова резко снижает свою эффективность, когда наблюдения группируются по малому количеству интервалов равнозначности. Например, при n = 200 количество интервалов должно быть не менее 20 (примерно по 10 наблюдений на каждый интервал в среднем). (3.1.11)
(3.1.11) (3.1.12)
(3.1.12) , (3.1.13).
, (3.1.13). - среднее арифметическое по «сырому» распределению; S - «сырое» стандартное отклонение;
- среднее арифметическое по «сырому» распределению; S - «сырое» стандартное отклонение; (3.1.15)
(3.1.15)
