 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод зон Френеля. Прямолинейное распространение света
В соответствии с принципом Гюйгенса-Френеля интенсивность света в точке Р определяется результатом интерференции всех вторичных волн, испущенных точками поверхности S. Для расчета результата интерференции Френель предложил мысленно разбить поверхность S на кольцевые зоны, которые и называются зонами Френеля. Они построены таким образом, чтобы расстояние от краев соседних зон до точки Р отличались на λ/2. В этом случае колебания, приходящие в т. Р от соответствующих частей соседних зон, будут иметь разность хода λ/2 и находиться в противофазе. Прономеруем зоны Френеля, начиная от центральной, индексом m (m = 1, 2, …) и обозначим амплитуду колебания, возбуждаемого в т. Р m-ой зоной, [ ]. Расстояние
Запишем выражение (33-1) в виде:
Вследствие монотонного убывания
Тогда выражения в скобках (33-2) будут равны нулю и, формула упрощается (число зон достаточно велико, а амплитуда последней зоны ничтожно мала по сравнению с амплитудой первой зоны).
Таким образом, амплитуда, создаваемая в некоторой точке Р всей сферической волновой поверхностью, равна половине амплитуды, создаваемой лишь одной центральной зоной. Так как величина зоны 1 мала (мала длина волны), то с точки зрения наблюдателя в точке Р, свет распространяется от источника Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластину, которая перекрывала бы четные или нечетные зоны, то интенсивность волн в т. Р резко возрастет (зонная пластинка).
Дифракция Френеля на круглом отверстии и диске.
Если m – мало, то Дифракционная картина представляет систему чередующихся темных и светлых колец.
Поиск по сайту: |








































 Пусть в некоторый произвольный момент времени фронт сферической волны, распространяется из источника
Пусть в некоторый произвольный момент времени фронт сферической волны, распространяется из источника  , занимает положение S (рис. 33.2).
, занимает положение S (рис. 33.2).
 . Можно показать, что площади зон Френеля примерно одинаковы
. Можно показать, что площади зон Френеля примерно одинаковы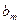 от зоны до точки Р медленно растет с номером зоны m. Угол φ между нормалью к элементам зоны и направлением на т. Р также растет с m. Все это приводит к тому, что амплитуда
от зоны до точки Р медленно растет с номером зоны m. Угол φ между нормалью к элементам зоны и направлением на т. Р также растет с m. Все это приводит к тому, что амплитуда 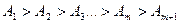 . Фазы колебаний, возбуждаемых соседними зонами, отличаются на π. Поэтому амплитуда А результирующего колебания в т. Р может быть представлена в виде:
. Фазы колебаний, возбуждаемых соседними зонами, отличаются на π. Поэтому амплитуда А результирующего колебания в т. Р может быть представлена в виде: (33-1)
(33-1) (33-2)
(33-2)



























 Пусть сферическая волна исходит из источника
Пусть сферическая волна исходит из источника 
 почти не отличается от
почти не отличается от