 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теория адсорбции ЛЭнгмюра
В основе этой теории лежат три положения: 1. Адсорбент представляет для адсорбата ограниченное число независимых адсорбционных мест. В каждом таком месте может адсорбироваться только одна молекула. Такие места могут существовать и при химической и при молекулярной адсорбции. В первом случае это отдельные ненасыщенные валентности поверхностных атомов адсорбента, во втором случае это площадки на поверхности или «пещерки» внутри адсорбента. Независимость мест означает, что адсорбция на одном месте не изменяет условия адсорбции на другом. В частности, это означает, что адсорбция на плоской поверхности должна осуществляться в одном слое (быть мономолекулярной), так как место во втором слое не может быть заполнено, если не заполнено находящееся под ним соответствующее место в первом слое. 2. Все адсорбционные места полагаются одинаковыми. В случае если адсорбция осуществляется на некоторой поверхности, то это положение означает однородность поверхности. 3. Между адсорбированными молекулами отсутствует взаимодействие. Для вывода изотермы адсорбции сделаем следующее: При равновесии скорость адсорбции (v¯) должна равняться скорости десорбции (v):
Для того чтобы молекула адсорбировалась, она должна удариться о поверхность и попасть на незанятое место. Так как число ударов пропорционально концентрации С, а вероятность попасть на незанятое место пропорционально их числу, то
где k1 – постоянная; q - доля занятых мест; следовательно, 1-q - доля незанятых мест. Молекула десорбируется, когда ее энергия окажется достаточной для того, чтобы оторваться от поверхности. Число таких молекул будет пропорционально общему числу адсорбированных молекул, поэтому:
где k2 – постоянная. Введем адсорбционный коэффициент K = k2/k1. Тогда, решая уравнение k1C(1-q)=k2q относительно q, получим
если использовать вместо концентрации С – величину парциального давления газа Р, уравнение (138) принимает вид
Анализ уравнения показывает, что при низких давлениях количество адсорбированного газа пропорционально его давлению
а при высоких давлениях, адсорбат стремиться заполнить все свободные места и q®1. При адсорбции из смеси n газообразных веществ аналогичный вывод приводит к уравнению
где КА- адсорбционный коэффициент реагента А; РА – парциальное давление вещества А. Адсорбционный коэффициент К зависит от температуры и от теплоты адсорбции (энергии взаимодействия адсорбата с поверхностью), которая в рамках изотермы Лэнгмюра принимается постоянной и независящей от заполнения:
где КА,0 – частотный множитель; QA – теплота адсорбции компонента А. Изотерма адсорбции Лэнгмюра имеет вид:
B
A Давление Р Рисунок 35. Изотерма адсорбции Лэнгмюра. На участке АВ при Р®0 изотерма близка к прямой линии, здесь справедливо уравнение Генри
Реакция, описываемая уравнением (143) имеет первый порядок. Однако область применения уравнения Генри мала. Уравнение Лэнгмюра неудовлетворительно описывает данные по физической адсорбции, что объясняется неоднородностью поверхности. Опытные данные показывают, что уравнение Фрейндлиха имеет более широкую область применимости, чем уравнение Лэнгмюра.
скорость адсорбции
где n < 1. Если w = x/m, где x – количество адсорбированного вещества, а m – масса адсорбента, то
Уравнение (146) в координатах lg(x/m) – lgP представляет собой прямую линию. Где n = tga и y = lgK.
lgP Рисунок 36. Изотерма Фрейндлиха в логарифмических координатах. Согласно уравнению Фрейндлиха, количество адсорбированного вещества неограниченно возрастает с увеличением давления. Поэтому при высоких степенях заполнения поверхности это уравнение является неудовлетворительным. Многие экспериментальные данные в области адсорбции и гетерогенного реагирования не описываются уравнением Лэнгмюра. При этом необходимо учитывать, что поверхность твердых тел либо энергетически неоднородна, либо между молекулами адсорбента на поверхности твердого вещества действуют силы ооталкивания. Для случая средних степеней заполнения поверхности Темкин вывел уравнение:
где f – константа; a0 – коэффициент адсорбции на наиболее сильно адсорбирующих участках; а1 – коэффициент адсорбции на наиболее слабо адсорбирующих участках.
Скорость адсорбции из уравнения Темкина при условии отсутствия торможения продуктами реакции и средним заполнением
В случае адсорбции на неоднородной поверхности значения не только теплот адсорбции, но и энергии активации адсорбции будут различаться. Для случая, когда Е линейно уменьшается с увеличением теплоты адсорбции (т.е. по мере заполнения поверхности), уравнение Темкина для среднего заполнения принимает вид
где a - отношение изменения теплоты адсорбции к изменению энергии активации (const). Скорость десорбции
Отсюда следует, что в случаях, когда лимитирующей стадией является адсорбция, скорость реакции пропорциональна давлению газообразного реагента (т.е. реакция имеет 1-й порядок). Скорость обратного процесса (десорбция) от давления не зависит. Если десорбция протекает медленней адсорбции, то скорость прямой реакции не зависит от давления газообразного продукта реакции. В последние годы большее практическое применение имеет теория БЭТ – Брунауэр – Эммет – Теллер, основанная на модели многослойной адсорбции. Уравнение БЭТ имеет вид
где Р – парциальное давление пара при t опыта; V – общий объем адсорбированного газа; Vm – объем адсорбированного газа, когда вся поверхность адсорбента покрыта сплошным молекулярным слоем. Согласно этому уравнению, графическая зависимость в координатах P/(V(P0-P)) – P/P0 представляет собой прямую линию.
P/P0 Рисунок 37. График зависимости изотермы адсорбции в координатах уравнения БЭТ.
где g – коэффициент; Q – теплота адсорбции ; L – теплота конденсации. Зная Vm – можно рассчитать удельную поверхность адсорбента
где N – число Авогадро; v - площадь, которую занимает каждая молекула в адсорбированном слое. v - можно вычислить, исходя из плотности вещества. Например, площадь занятая молекулами N2 при –1950С = 16,2 А0, в предположении, что все молекулы имеют сферическую форму и соприкасаются друг с другом. Таким образом, из измеренного значения Vm можно вычислить площадь поверхности адсорбента. Этот метод нашел широкое применение при определении площади поверхности твердых адсорбентов, в том числе и для характеристики самых различных порошкообразных веществ урановой технологии и количественного описания их реакционной способности. Нередко скорость гетерогенных реакций относят к определенной по методу БЭТ поверхности твердого реагента. Роль адсорбционных и десорбционных стадий гетерогенных процессов урановых производств начали изучать сравнительно недавно, поэтому большинство систем еще не исследовано. Известно, что кислород очень быстро сорбируется свежевосстановленной поверхностью UO2. Начиная с – 1850 С кислород хемосорбируется на UO2, покрывая поверхность мономолекулярным слоем. Между – 130 и +500 С поверхность двуокиси урана окисляется на глубину 50 А0. Это связано с тем, что поверхность окисления представляет собой нестехиометрический оксид, где избыточный кислород внедряется в междоузлия решетки. Степень окисления зависит от удельной поверхности порошка, что несомненно указывает на адсорбционный характер процесса. Объемное окисление UO2 начинается с 600 С как в атмосфере кислорода, так и на воздухе.
ЛЕКЦИЯ 14
Поиск по сайту: |
 .
. ,
, ,
, , (138)
, (138)
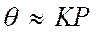 (139)
(139)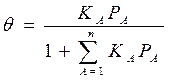 (140)
(140) (141)
(141) q
q
 qmax
qmax (142)
(142) (143)
(143) (144)
(144) (145)
(145) или
или  (146)
(146) lg(x/m)
lg(x/m)
 y a
y a
 , (147)
, (147) - для случая средне адсорбирующих участков ,
- для случая средне адсорбирующих участков , - для случая слабо адсорбирующих участков (закон Генри)
- для случая слабо адсорбирующих участков (закон Генри)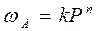 , где 0 < n< 1.
, где 0 < n< 1. , (148)
, (148) (149)
(149) (150)
(150)


 y a
y a ;
; 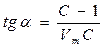 ;
;  ,
, , (151)
, (151)