 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ТЕМА: «КИНЕМАТИКА ПРЯМОЛИНЕЙНОГО И КРИВОЛИНЕЙНОГО ДВИЖЕНИЯ»
Для математического описания прямолинейного и криволинейного движения имеются 2 группы величин: линейные и угловые:
Все кинематические уравнения, необходимые для решения задач по данной теме, можно свести следующей таблице:
Отдельного внимания заслуживает линейное ускорение при криволинейном движении:
О
Полное линейное ускорение есть векторная сумма нормального и тангенциального ускорения:
Для этого равенства верно: Отсюда следует:
Для решения задач еще необходимы формулы, связывающие между собой угловые и линейные величины: S = φr υ = ωr, at = εr ,
Также по этой теме понадобятся следующие формулы: φ = 2πN, где N – количество оборотов, совершенных телом; ω = 2πν, гдеν – частота вращения
Рассмотрим примеры решения некоторых типовых задач.
ЗАДАЧА 1 Частота врещения шкива за 0,5 минуты изменилась от 180 об/мин до 120 об/мин. Определить угловое ускорение ε и количество оборотов N, которые совершил шкив за это время. Движение считать равозамедленным. Дано:
νо = 180 об/мин = 180 ν = 120 об/мин = 120
ε - ? N - ?
Для случая замедленного вращения выбираем знак «-»:
Чтобы найти ε в(2) подставим выражения ω = 2πν, ωо = 2πνо:
2πν = 2πνо – εt Найдем ε: εt=2πνо-2πν εt=2π(νо-ν)
N будем искать из (1), учитывая, что φ = 2πN:
2πN = 2πνоt -
Ответ: ε = 0,21 об/с2, N = 75 об.
ЗАДАЧА 2 Залежність кутової швидкості матеріальної точки від часу визначається рівнянням: ω(t)=0,1t2+0,5t+50. Визначити: 1). Швидкість υна 5-й секунді, якщо радіус обертання дорівнює 20 см; 2). Кутове прискорення прискорення εчерез 0,5 хвилини від початку руху; 3). Кут обертання тіла φ з 20-ї до 30-ї секунди руху.
ω(t)=0,1t2+0,5t+50 1). Знайдемо υ: υ = ωr r = 20 см = 0,2 м t1= 5 с Кутова швидкість на 5-й секунді дорівнює: t2= 30 с t3= 20 с t4= 30 с Тогда: υ - ? ε- ? φ - ? 2). Знайдемо ε:
Для часу t2= 0,5:
3).Знайдемо φ:
Відповідь:
Поиск по сайту: |


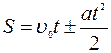

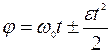
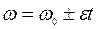


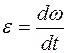

 рис. 1.6
рис. 1.6



 .
.

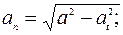
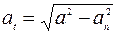
 ,
, 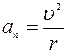 , an = ω2r.
, an = ω2r.
 t = 0,5 мин = 30 с
t = 0,5 мин = 30 с = 3 об/с Воспользуемся уравнениями равноускоренного
= 3 об/с Воспользуемся уравнениями равноускоренного Решив их совместно, найдем искомые величины.
Решив их совместно, найдем искомые величины.

 (1)
(1) (2)
(2) .
.

 .
. (об).
(об). Дано:
Дано: (рад/с)
(рад/с) ;
; 
 ;
; (рад/с2);
(рад/с2); (рад/с2).
(рад/с2).


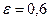 рад/с2;
рад/с2; 