 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема о скоростях точек плоской фигуры
Движение плоской фигуры складывается из поступательного движения, при котором все точки фигуры движутся так же, как и полюс и вращательного движения вокруг полюса. Покажем, что скорость любой точки плоской фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений. Дана плоская фигура, расположенная в плоскости Оху (рис. 35).
Положение полюса А определяется радиусом-вектором
где Продифференцировав данное равенство по времени, получим выражение для скорости точки В: где
Так как
скорость любой точки плоской фигуры геометрически складывается из скорости какой-либо другой точки, принятой за полюс, и скорости этой точки при вращении фигуры вокруг полюса. Следовательно, скорость некоторой точки В плоской фигуры изображается диагональю векторного параллелограмма (построенного при точке В), в котором его сторонами являются векторы
Рис. 36. К доказательству теоремы о скоростях точек плоской фигуры
Модуль скорости точки В (или любой другой точки плоской фигуры) можно найти следующими способами: · графически (по правилу треугольника или параллелограмма); · аналитически, используя теорему косинусов:
· способом проекций: где vBx, vBy – проекции скорости точки В на заранее выбранные оси х и у декартовой системы координат.
Теорема о равенстве проекций скоростей точек
Модуль скорости точки В можно также определить, используя теорему о скоростях точек плоской фигуры, спроецировав векторное равенство
Поиск по сайту: |

 . Тогда положение точки В это фигуры можно определить как векторную сумму:
. Тогда положение точки В это фигуры можно определить как векторную сумму: ,
, – вектор, определяющий положение точки В относительно полюса А.
– вектор, определяющий положение точки В относительно полюса А. ,
, – скорость полюса А,
– скорость полюса А, – скорость точки В относительно полюса А.
– скорость точки В относительно полюса А. , то
, то  меняется только по направлению. Это означает, что точка В совершает вращение вокруг полюса А. Поэтому
меняется только по направлению. Это означает, что точка В совершает вращение вокруг полюса А. Поэтому  и
и  . Таким образом, получаем формулу, выражающую теорему о скоростях точек плоской фигуры:
. Таким образом, получаем формулу, выражающую теорему о скоростях точек плоской фигуры:
 , перпендикудярный отрезку АВ и сонаправленный с угловой скоростью ω, и
, перпендикудярный отрезку АВ и сонаправленный с угловой скоростью ω, и 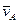 (рис. 36).
(рис. 36).
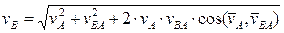 .
. ,
, на прямую АВ (рис. 37):
на прямую АВ (рис. 37): Проекции скоростей
Проекции скоростей  двух точек А и В твердого тела на прямую АВ, соединяющую эти точки, равны (рис. 37).
двух точек А и В твердого тела на прямую АВ, соединяющую эти точки, равны (рис. 37).
