 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Робота і потужність сили ⇐ ПредыдущаяСтр 5 из 5
Для характеристики дії сили, що діє на тіло при деякому його переміщенні, вводиться поняття про роботу сили. Розглянемо прямолінійний рух тіла M уздовж осі Ох під дією змінної сили F(x) з положення х0 в положення х1 (рис. 7.22). Прикладом змінної сили, яка залежить від переміщення х, є сила пружності пружини
де с – жорсткість пружини, х – деформація цієї пружини. Іншими прикладами таких сил є сила усесвітнього тяжіння, сила Кулона взаємодії між зарядами, ці сили залежать від відстані між тілами (зарядами).
Рис. 7.22. Введемо спочатку поняття про елементарну роботу сили F на нескінченно малому переміщенні
Робота сили на будь-якому кінцевому переміщенні як інтегральна сума відповідних елементарних робіт рівна
Одиницею виміру роботи в системі СІ є джоуль (1 дж = 1 н м). Потужність. Потужністю називається величина, що визначає роботу, яку виконує сила за одиницю часу. Якщо робота здійснюється рівномірно, то потужність є
де t – час, протягом якого вироблена робота. У загальному випадку
де v – швидкість тіла. Одиницею виміру потужності в системі СІ є ват (1 Вт = 1 дж/сек). Роботу, яку призводить машина, вимірюється добутком її потужності на час роботи. Звідси в техніці виникла одиниця виміру роботи кіловат. Приклади.1) Обчислити роботу, яку необхідно витратити, щоб підняти тіло маси m з поверхні Землі на висоту h (радіус Землі R = 6400км). За допомогою отриманого результату визначити другу космічну швидкість (швидкість, при якій тіло, що вертикально піднімається, може піднятися на будь-яку висоту). Розв‘язання.На ракету, що має масу m, за законом усесвітнього тяжіння діє сила Шукана робота сили тяжіння при виводі ракети з поверхні Землі на висоту h дорівнює
або, враховуючи значення прискорення вільного падіння, маємо
В той же час робота дорівнює зміні кінетичній енергії ракети
Аби розрахувати другу космічну швидкість, яку треба надати ракеті на поверхні Землі для подолання земного тяжіння, потрібно перейти до границі h → ∞ у останньому виразу
2)Обчислити роботу, яку треба витратити, щоб розтягнути пружину, яка знаходиться в положенні рівноваги, на 10 см. Відомо, що при розтягуванні пружини на 1 см сила натягнення дорівнює 5 Н.
Рішення.Пружна сила, з якою діє пружина на тіло, підкоряється закону Гуку, згідно якому F = с x, де с – жорсткість пружини, а х – подовження пружини. З умови задачі знаходимо жорсткість пружини с. Оскільки при розтягуванні пружини на 0,01 м сила пружного натягнення рівна 5 Н, то 5 Н = с ∙ 0,1 м. Отже, с = 500 Н /м і сила пружності пружини дорівнює F(x)= 500 x, Н Шукана робота сили пружності при розтягуванні пружини на 10 см = 0,1 м обчислюється за формулою:
Невласні інтеграли Визначний інтеграл Невласний інтеграл I роду (інтеграл з нескінченним проміжком інтегрування) Хай підінтегральна функція f(x) безперервна і обмежена для всіх
Якщо ця границя існує і вона кінцева, то невласний інтеграл Аналогічним чином визначається невласний інтеграл на проміжку
Невласний інтеграл з двома нескінченними границями визначається формулою
де с – довільне число. В даному випадку інтеграл зліва збігається у тому випадку, коли збігаються обоє інтеграла справа. Приклади.Обчислити невласні інтеграли або встановити їх розбіжність: 1. 2. = 3. 4. Визначити площу фігури, обмеженою кривою
=
Рис. 7.19. Ознаки порівняння Приведемо без доведення одну з ознак збіжності невласних інтегралів I роду. Теорема.Якщо на проміжку Приклад.Досліджувати збіжність інтеграла Невласний інтеграл II роду (інтеграл від розривної функції) Хай функція f(x) безперервна на проміжку
Якщо границя в правій частині існує, то невласний інтеграл Якщо функція f(x) має розрив в точці с на проміжку [а, b], то невласний інтеграл II роду визначається формулою
В цьому випадку інтеграл зліва збігається, якщо обоє невласних інтеграла справа збігаються. Приклади.Обчислити або встановити збіжність невласного інтеграла: 1.
2.
інтеграл розбігається. Приклади для самостійного розв‘язання Обчислити невласні інтеграли: 1) 5)
Поиск по сайту: |
 , (7.17)
, (7.17)

 .
. . (7.18)
. (7.18) , (7.19)
, (7.19) , (7.20)
, (7.20) , де G – гравітаційна постійна; M – маса Землі; m – маса ракети; x – відстань ракети до центру Землі,
, де G – гравітаційна постійна; M – маса Землі; m – маса ракети; x – відстань ракети до центру Землі,  = 9,81 м/с2 - прискорення вільного падіння.
= 9,81 м/с2 - прискорення вільного падіння.

 , враховуючи, що стартова кінетична енергія дорівнює нулю, а V – швидкість ракети на висоті h над поверхнею Землі. Таким чином, швидкість ракети V на висоті h визначається з рівняння
, враховуючи, що стартова кінетична енергія дорівнює нулю, а V – швидкість ракети на висоті h над поверхнею Землі. Таким чином, швидкість ракети V на висоті h визначається з рівняння , звідки
, звідки  .
. (м/с).
(м/с).

 називають власним інтегралом, якщо проміжок інтегрування кінцевий, а підінтегральна функція f(x) безперервна на цьому відрізку. У даному розділі розглядаються так звані невласні інтеграли, тобто визначний інтеграл від безперервної функції, але з нескінченним проміжком інтеграції, або визначний інтеграл з кінцевим проміжком інтегрування, але від функції, що має в цьому інтервалі нескінченний розрив.
називають власним інтегралом, якщо проміжок інтегрування кінцевий, а підінтегральна функція f(x) безперервна на цьому відрізку. У даному розділі розглядаються так звані невласні інтеграли, тобто визначний інтеграл від безперервної функції, але з нескінченним проміжком інтеграції, або визначний інтеграл з кінцевим проміжком інтегрування, але від функції, що має в цьому інтервалі нескінченний розрив. . Невласний інтеграл першого роду позначається як
. Невласний інтеграл першого роду позначається як  . Невласним інтегралом І роду від функції f(x) на нескінченному проміжку
. Невласним інтегралом І роду від функції f(x) на нескінченному проміжку  називається границя, якщо вона існує, при
називається границя, якщо вона існує, при  визначного інтеграла
визначного інтеграла  , тобто
, тобто
 =
=  . (7.22)
. (7.22) =
=  +
+  , (7.23)
, (7.23) =
= 

 , інтеграл розбігається;
, інтеграл розбігається; =
=  =
= 
 =
= ;
; =
= 

 , інтеграл розбіжний, оскільки при
, інтеграл розбіжний, оскільки при  не існує.
не існує. і віссю Ох
і віссю Ох  =
=  =
= 
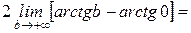
 .
.
 для безперервних функцій задовольняється нерівність 0
для безперервних функцій задовольняється нерівність 0  , то із збіжності інтеграла
, то із збіжності інтеграла 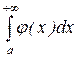 виходить збіжність інтеграла
виходить збіжність інтеграла  . Підінтегральна функція
. Підінтегральна функція  на проміжку інтегрування менше ніж
на проміжку інтегрування менше ніж  , а інтеграл
, а інтеграл  сходиться. Отже, даний інтеграл також збігається.
сходиться. Отже, даний інтеграл також збігається. і має нескінченний розрив в точці х = b . Невласним інтегралом II роду називається кінцева границя, якщо вона існує, інтеграла
і має нескінченний розрив в точці х = b . Невласним інтегралом II роду називається кінцева границя, якщо вона існує, інтеграла  . Таким чином, за визначенням
. Таким чином, за визначенням . (7.18)
. (7.18) збігається. Інакше невласний інтеграл розбігається.
збігається. Інакше невласний інтеграл розбігається. .
. . При х = 1 функція
. При х = 1 функція  має нескінченний розрив.
має нескінченний розрив.

 . При х = 0 функція
. При х = 0 функція  має нескінченний розрив.
має нескінченний розрив.


 ,
, . 2)
. 2)  . 3)
. 3) 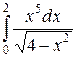 . 4)
. 4)  .
. . 6)
. 6)  .
.