 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методи інтегрування: заміна змінної інтегрування, інтегрування частинами
I. Розглянемо метод заміни змінної інтегрування, який дозволяє у багатьох випадках зводити інтеграли до табличних або таких, спосіб інтегрування яких уже відомий. Він базується на виконанні застосуванні наступної теореми: Теорема. Нехай Тоді При обчисленні конкретного інтеграла будемо користуватисяробочою формулою: тут Успіх інтегрування методом заміни змінної значною мірою залежить від того, наскільки вдало виконано заміну змінних, яка спрощує даний інтеграл. Разом з тим, не можна дати одне загальне правило для вибору підстановки. Уміння підбирати функцію для заміни досягається достатньою кількістю зроблених самостійно вправ. Для певного класу інтегралів доцільні підстановки розроблені і будуть далі пропонуватися. Зауваження. Інколи буває раціонально проводити заміну не змінної інтегрування Якщо інтеграл II. Суть методу інтегрування частинами полягає у застосуванні формули
яку називають формулою інтегрування частинами. Її застосування доцільне у тих випадках, коли другий інтеграл формули (4) буде простішим за перший або буде йому подібним. Для використання формули інтегрування частинами до деякого інтеграла 1) Якщо підінтегральна функція має вигляд 2)Якщо підінтегральна функція містить, як множник, функції III. Класифікуючи елементарні функції, виділяють важливий клас раціональних функцій,які подаються у вигляді відношення многочленів I. II. Тут І. ІІ. ІІІ.
тобто
Зауваження. За допомогою тієї ж заміни ІV.
Останній інтеграл
при цьому
Формула (9) дозволяє обчислити Приклад 1 Обчислити інтеграли, застосовуючи метод заміни змінної: 1) 5) 9) Розв’язання 1) Такого інтеграла серед табличних немає. Спробуємо обчислити цей інтеграл, зробивши заміну змінної інтегрування
Скористаємось 2-м табличним інтегралом, тому що підінтегральна функція має вигляд
повертаємось до старої змінної інтегрування
2)
3) Обчислюючи цей інтеграл, на відміну від попередніх, зробимо заміну не змінної інтегрування
4)
5)
6)
7)
8)
9)
10)
Приклад 2 Обчислити інтеграли: 1) 5) 9) Розв'язання 1) Очевидно підінтегральна функція являє собою добуток многочлена 2-ї степені
Очевидно, що одержаний останній інтеграл простіший за вихідний, так як маємо уже многочлен першої степені. Для обчислення цього інтеграла за тією ж формулою (16.4) знову виберемо
2)
3)
4)
5)
6)
7)
8)
9)
10)
11) Проінтегрувавши два рази частинами, дістанемо лінійне рівняння відносно вихідного інтеграла
Таким чином, дістали лінійне рівняння відносно
Таким чином,
Приклад 3 Обчислити інтеграли від найпростіших раціональних дробів: 1) 5) 9)
Розв’язання
1) 2) 3) 4)
5) Приведемо цей інтеграл до табличних інтегралів (3) та (13) (або(14)), проводячи заміну
Інтеграл обчислений. 6)
Інтегрування завершено. 7)
8)
9)
10)
Приклад 4 Обчислити інтеграли: 1) 1)Аналогічно попередньому прикладу робимо заміну
За рекурентною формулою (16.9), покладаючи
Обчислюємо останній інтеграл за рекурентною формулою (9) при
Робимо обернену заміну
2)
Перший інтеграл – це 2-й табличний, а другий обчислюємо за рекурентною формулою (9) при
Повертаємось до старої змінної, покладаючи
3)
Для обчислення інтегралів використовуємо 2-й табличний та формулу (9) при
Обчислюємо останній інтеграл за рекурентною формулою (9) при
Робимо обернену заміну
Завдання для самостійної роботи: Завдання 1.Обчислити інтеграли, застосовуючи метод заміни змінної.
1) 5) 9) 13) 17) 21) 25) 29) 33) Відповіді:
1) 3) 5) 7) 9) 10) 12) 14) 16) 18) 20) 22) 24) 25) 27) 29) 31) 33) Завдання 2.Обчислити інтеграли, застосувавши метод інтегрування частинами:
1) 3) 5) 7) 9) 11) 13) 15) 17) 19) 21) 23) 25) 27) 29) 31) 33) 35) 37)
Відповіді:
1) 3) 5) 7) 8) 10) 12) 14) 16) 18) 20) 21) 22) 23) 24) 26) 27) 29) 30) 31) 32) 33) 34) 35) 36) 37)
Поиск по сайту: |
 ,
,  і функція
і функція 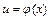 диференційовна на проміжку
диференційовна на проміжку 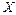 та відображає
та відображає 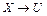 .
. (1)
(1)
 , (2)
, (2) - обернена функція до функції
- обернена функція до функції 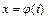 .
. , а деякої функції від неї
, а деякої функції від неї 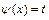 . З цієї рівності знаходять
. З цієї рівності знаходять  і проводять підстановку
і проводять підстановку (3)
(3)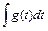 простіший за попередній, то проведена підстановка досягла мети. Інтеграл обчислюють і після цього повертаються до старої змінної інтегрування
простіший за попередній, то проведена підстановка досягла мети. Інтеграл обчислюють і після цього повертаються до старої змінної інтегрування  .
.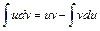 , (4)
, (4) потрібно підінтегральний вираз
потрібно підінтегральний вираз  записати у вигляді добутку двох множників
записати у вигляді добутку двох множників  та
та  .Зробимо рекомендації по їх вибору.
.Зробимо рекомендації по їх вибору.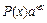 ,
,  ,
, 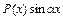 ,
,  , де
, де 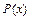 - многочлен від
- многочлен від  , а все останнє разом з
, а все останнє разом з  і знову знижуємо степінь многочлена на одиницю і т.д.
і знову знижуємо степінь многочлена на одиницю і т.д. ,
, 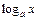 ,
,  ,
, 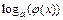 ,
,  ,
, 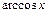 ,
,  , то якщо за
, то якщо за  . Виділимо з класу раціональних функцій (або раціональних дробів) основні найпростіші дроби. Вони бувають чотирьох типів:
. Виділимо з класу раціональних функцій (або раціональних дробів) основні найпростіші дроби. Вони бувають чотирьох типів: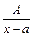 ; III.
; III. 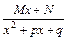 ,
, 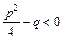 ;
;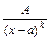 ; IV.
; IV. 
 ;
; – дійсні числа,
– дійсні числа, 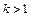 – ціле число. Розглянемо способи інтегрування основних дробів.
– ціле число. Розглянемо способи інтегрування основних дробів.
 ; (5)
; (5)
 ;
;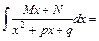


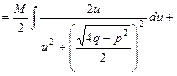

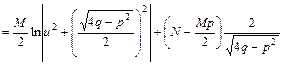
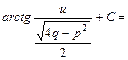

 ,
,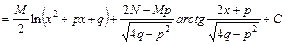 (7)
(7)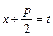 можна так само обчислювати інтеграли виду
можна так само обчислювати інтеграли виду  і у тих випадках, коли
і у тих випадках, коли 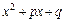 є повним квадратом або
є повним квадратом або 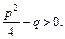 У цих випадках при обчисленні 2-го інтегралу замість табличного (13), як було вище зроблено, треба користуватися відповідно табличними інтегралами (2) та (14).
У цих випадках при обчисленні 2-го інтегралу замість табличного (13), як було вище зроблено, треба користуватися відповідно табличними інтегралами (2) та (14).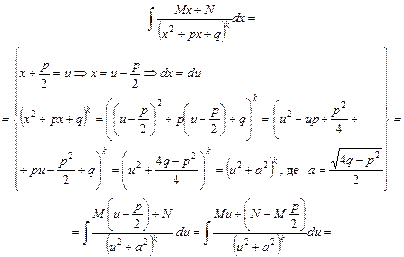
 (8)
(8) обчислюється з використанням рекурентної формули
обчислюється з використанням рекурентної формули ,
,  (9)
(9) .
.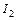 , знаючи
, знаючи 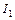 , потім обчислити
, потім обчислити  , знаючи
, знаючи 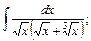 2)
2) 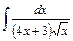 ; 3)
; 3)  4)
4)  ;
; ; 6)
; 6) 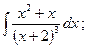 7)
7) 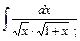 ; 8)
; 8) 
 10)
10) 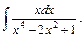

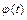 виберемо степеневу функцію
виберемо степеневу функцію 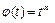 і
і  підберемо таким, щоб добувались усі корені підінтегральної функції після підстановки туди
підберемо таким, щоб добувались усі корені підінтегральної функції після підстановки туди  . Таким очевидно є
. Таким очевидно є 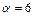 . Тоді заміна має вигляд
. Тоді заміна має вигляд 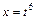
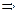
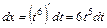 Обернена заміна
Обернена заміна  Усі ці допоміжні записи розміщують у фігурних дужках (дивись робочу формулу (16.2)) так, як це зроблено нижче:
Усі ці допоміжні записи розміщують у фігурних дужках (дивись робочу формулу (16.2)) так, як це зроблено нижче: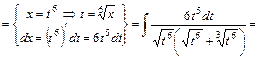

 , дістанемо
, дістанемо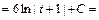

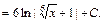

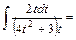
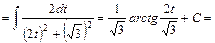
 .
.
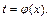 Щоб підінтегральна функція перетворилась в інтеграл від многочленна, зробимо заміну
Щоб підінтегральна функція перетворилась в інтеграл від многочленна, зробимо заміну  , (хоча кращою могла б бути заміна
, (хоча кращою могла б бути заміна  ).
).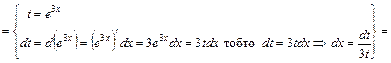


 .
.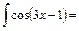
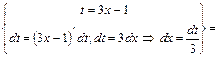
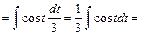
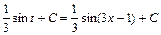 .
.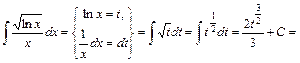
 .
.


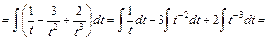
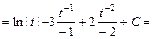
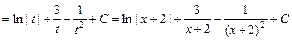 .
.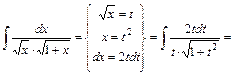
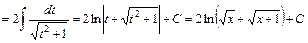 .
.
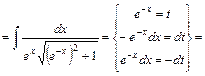

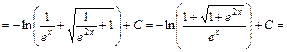

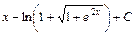 .
.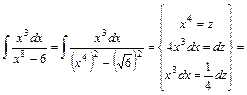
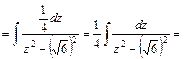
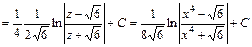 .
.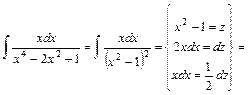
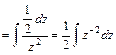
 .
.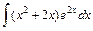 ; 2)
; 2) 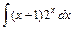 ; 3)
; 3) 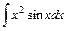 ; 4)
; 4)  ;
;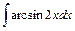 ; 6)
; 6) 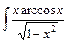 ; 7)
; 7)  ; 8)
; 8) 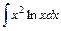 ;
; ; 10)
; 10)  ; 11)
; 11) 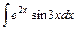 .
.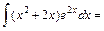
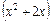 на показникову функцію
на показникову функцію 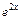 . Згідно даним рекомендаціям, виберемо
. Згідно даним рекомендаціям, виберемо  ,
,  та використаємо формулу (16.4). Допоміжні записи проводяться у фігурних дужках так, як це зроблено нижче.
та використаємо формулу (16.4). Допоміжні записи проводяться у фігурних дужках так, як це зроблено нижче.

 ,
, 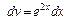 і всі допоміжні записи помістимо у фігурні дужки:
і всі допоміжні записи помістимо у фігурні дужки: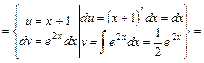
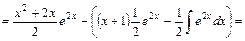
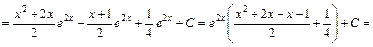
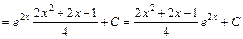 .
.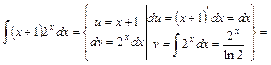

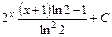 .
.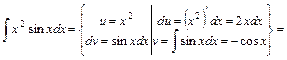
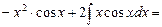




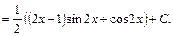
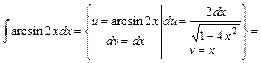

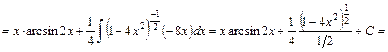
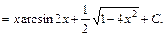
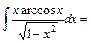


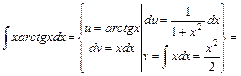
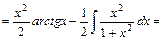
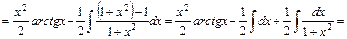
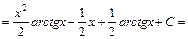
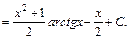

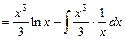
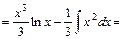
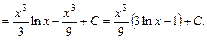



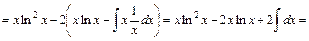
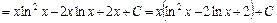 .
.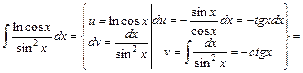



 . Розв'язавши його відносно
. Розв'язавши його відносно  , знайдемо шуканий інтеграл.
, знайдемо шуканий інтеграл.
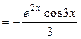
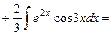
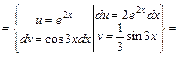
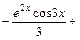
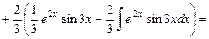
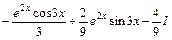 .
.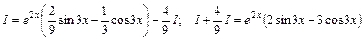



 .
.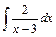 ; 2)
; 2) 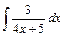 ; 3)
; 3)  ; 4)
; 4) 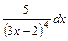 ;
; ; 6)
; 6) 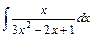 ; 7)
; 7)  ; 8)
; 8) 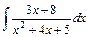 ;
; ; 10)
; 10) 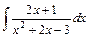 .
.
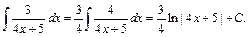
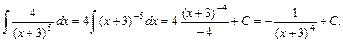
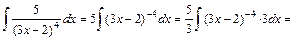
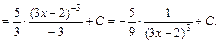

 (див. (7)). Тут
(див. (7)). Тут  - другий коефіцієнт квадратного тричлена знаменника
- другий коефіцієнт квадратного тричлена знаменника 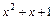 , де
, де 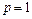 ,
, 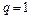 , тому зміна
, тому зміна 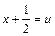 .
.

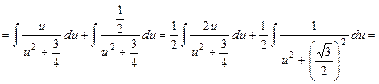




 .
.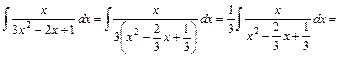


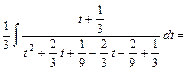
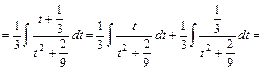
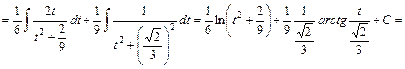



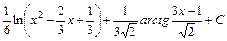 .
.



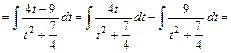



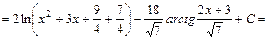
 .
.

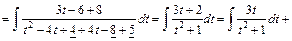
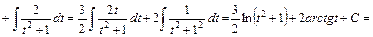
 .
.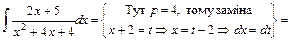


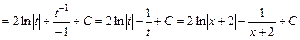 .
.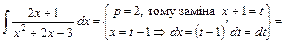


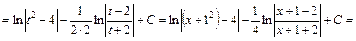
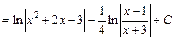 .
.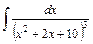 ; 2)
; 2) 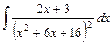 ; 3)
; 3) 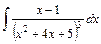 .
.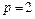 .
.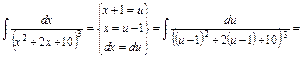
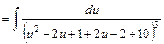
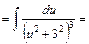
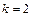 , маємо:
, маємо:

 :
: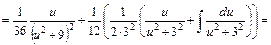
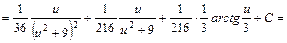



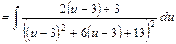


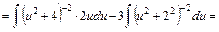


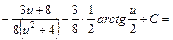
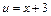 , дістаємо
, дістаємо
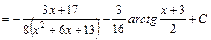 .
.
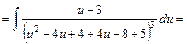




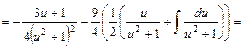
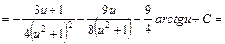
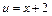 , дістаємо:
, дістаємо: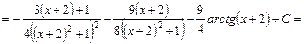

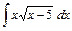 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 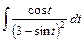 ;
; ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ;
; ; 10)
; 10)  ; 11)
; 11) 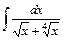 ; 12)
; 12)  ;
;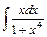 ; 14)
; 14) 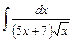 ; 15)
; 15) 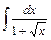 ; 16)
; 16)  ;
;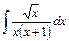 ; 18)
; 18) 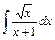 ; 19)
; 19) 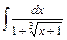 ; 20)
; 20) 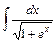 ;
;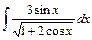 ; 22)
; 22)  ; 23)
; 23)  ; 24)
; 24) 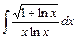 ;
; ; 26)
; 26)  ; 28)
; 28)  ;
;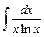 ; 30)
; 30)  ; 31)
; 31)  ; 32)
; 32)  ;
;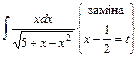 ; 34)
; 34) 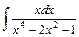 .
. ; 2)
; 2) 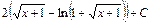 ;
;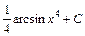 ; 4)
; 4)  ;
; ; 6)
; 6) 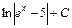 ;
; ; 8)
; 8)  ;
;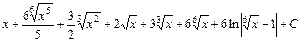 ;
;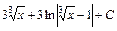 ; 11)
; 11) 
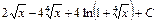 ;
; ; 13)
; 13)  ;
;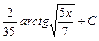 15)
15)  ;
; ; 17)
; 17) 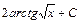 ;
;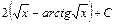 ; 19)
; 19)  ;
;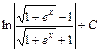 ; 21)
; 21) 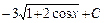 ;
;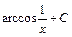 ; 23)
; 23)  ;
; ;
; ; 26)
; 26) 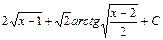 ; 28)
; 28) 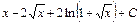 ;
; ; 30)
; 30) 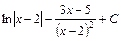 ;
;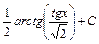 ; 32)
; 32)  ;
; ; 34)
; 34) 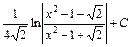 .
. ; 2)
; 2)  ;
;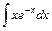 ; 4)
; 4) 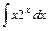 ;
;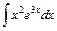 ; 6)
; 6) 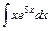 ;
; ; 8)
; 8)  ;
;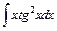 ; 10)
; 10) 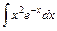 ;
; ; 12)
; 12) 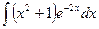 ;
; ; 14)
; 14)  ;
; ; 16)
; 16)  ;
;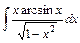 ; 18)
; 18)  ;
;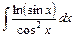 ; 20)
; 20) 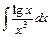 ;
;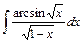 ; 22)
; 22)  ;
;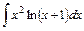 ; 24)
; 24)  ;
;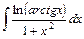 ; 26)
; 26)  ;
; ; 28)
; 28) 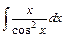 ;
; ; 30)
; 30)  ;
; ; 32)
; 32) 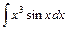 ;
;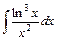 ; 34)
; 34) 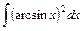 ;
;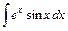 ; 36)
; 36) 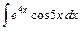 ;
;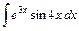 .
.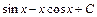 ; 2)
; 2) 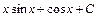 ;
;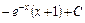 ; 4)
; 4)  ;
; ; 6)
; 6)  ;
;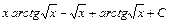 ;
; ; 9)
; 9) 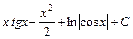 ;
;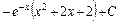 ; 11)
; 11)  ;
; ; 13)
; 13)  ;
; ; 15)
; 15)  ;
; ; 17)
; 17)  ;
;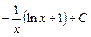 ; 19)
; 19) 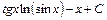 ;
; ;
; ;
; ;
;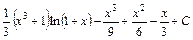 ;
; ; 25)
; 25)  ;
;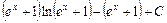 ;
; ; 28)
; 28) 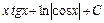 ;
;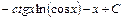 ;
;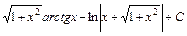 ;
;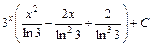 ;
; ;
; ;
; ;
;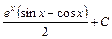 ;
;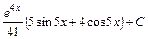 ;
;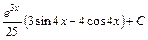 .
.