 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Середні рівні ряду динамікиСтр 1 из 3Следующая ⇒
Зміст вступ.. 4 1. предмет аналізу рядів динаміки.. 4 2. зімкнення рядів динаміки.. 5 3. середні рівні ряду динаміки.. 6 4. аналіз рядів динаміки.. 6 5. виявлення тенденції ряду динаміки.. 11 6. ЕКСТРАПОЛЯЦІЯ ПОКАЗНИКІВ РЯДУ ДИНАМІКИ.. 14 7. ГРАФІЧНА ПОБУДОВА ЛІНІЇ ТРЕНДУ.. 15 8. висновок.. 16 9. оформлення роботи.. 17 список рекомендованої літератури.. 18 Вступ Методичні вказівки призначенідля практичного освоєння теоретичного курсу статистики з теми “Ряди динаміки” на конкретному прикладі в процесі виконання курсової роботи. Письмове виконання курсової роботи сприяє не тільки поглибленому вивчанню методів статистики, але й придбанню практичних навичок з розрахунку статистичних показників, правильної побудови й оформлення таблиць, графіків. Основна мета розробок – навчити розумінню суті розрахункових показників та їхнього аналізу. Керівник курсової роботи видає студентові завдання з вихідними даними, у т.ч. - на тему “Ряди динаміки”, і встановлює порядок, обсяг і термін завершення розрахунків, аналізу і підготовки до захисту. Керівник роботи: - контролює процес виконання роботи; - рекомендує літературу і довідкові матеріали; - проводить консультації зі студентами; - допомагає в обробці вихідних даних і в складанні висновків; - перевіряє виконані розрахунки. Перед рішенням кожної задачі необхідно ретельно вивчити її зміст. Перш ніж приступати до практичного виконання завдань, варто уважно ознайомитися із відповідним матеріалом методичних вказівок та літературою з рекомендованого списку .
Предмет аналізу рядів динаміки Систематизовані в хронологічному порядку дані називають рядами динаміки. Кожен ряд динаміки складається: - з періодів, або моментів часу t, до яких належать рівні ряду, - статистичних показників у, які характеризують рівні часу. Завдання статистики в межах розглянутої теми полягає в тому, щоб шляхом аналізу рядів динаміки розкрити та охарактеризувати закономірності, що проявляються на різних етапах розвитку того чи іншого явища, виявити тенденції розвитку та їхні особливості. Зімкнення рядів динаміки У деяких випадках виникає необхідність зімкнення рядів динаміки (табл. 1). Таблиця 3.1
Виконаємо зімкнення ряду динаміки обсягів виробництва будівельної корпорації, млн.грн., якщо корпорація до 2006 р. поєднувала 5 управлінь, а з 2006 р. — 8. Для цього потрібно визначити коефіцієнт співвідношення двох статистичних рівнів динамічних рядів: К2006 = 240/150 = 1,6. Тоді отримуємо значення рівнів: - для 8 управлінь: 120*1,6 = 192; 135*1,6 = 216. - для 5 управлінь: 272/*1,6 = 170; 300/1,6 = 187,5.
Результати формування відновленого ряду динаміки обсягів будівництва оформлюємо в таблицю 2.
Таблиця 3.2
середні рівні ряду динаміки Ряди динаміки поділяються на моментні (значення показників приводяться на початок місяців, кварталів, років) та інтервальні (показники за місяці, за квартали, за роки). Середній рівень для інтервального ряду динаміки з рівновіддаленими датами розраховується за допомогою середньої арифметичної простої:
Середній рівень для моментного ряду динаміки з рівновіддаленими датами розраховується за допомогою середньої хронологічної:
Аналіз рядів динаміки Під час аналізу рядів динаміки обчислюють і використовують такі аналітичні показники динаміки: абсолютний приріст, темп зростання, темп приросту і абсолютне значення одного проценту приросту. Обчислення цих показників ґрунтується на абсолютному або відносному співставленні рівнів ряду динаміки. Розрахунок показників динаміки ґрунтується на порівнянні рівнів динамічного ряду. Якщо база порівняння постійна, характеристики динаміки називають базисними, якщо база порівняння змінна - ланцюговими. Абсолютний приріст (зменшення) Dу - це різниця рівнів динамічного ряду. Абсолютні зміни характеризують збільшення або зменшення рівня ряду за визначений проміжок часу. Абсолютний ланцюговий приріст:
де у - значення вихідних даних.
Абсолютний базисний приріст:
де yо - значення базисного значення (звичайно значення за 1-ий період).
Між базисними і ланцюговими абсолютними приростами існує взаємозв'язок: сума абсолютних ланцюгових приростів усіх рядів дорівнює базисному абсолютному приростові останнього періоду ряду. Тобто:
15+15+20+17,5 = 67,5. 67,5 = 67,5. Темп (коефіцієнт) зростання розраховується як відношення рівнів ряду. Коефіцієнт зростання (Кз) характеризує співвідношення двох рівнів ряду. Він показує, у скільки разів порівнюваний рівень більше рівня, прийнятого за постійну базу порівняння. Коефіцієнт зростання, виражений у відсотках, називається темп зростання (Тз). Ланцюговий темп зростання:
Базисний темп зростання:
Між базисними і ланцюговими коефіцієнтами зростання існує взаємозв'язок: добуток послідовних ланцюгових коефіцієнтів зростання дорівнює кінцевому базисному коефіцієнту зростання.
К з = 1,125*1,111*1,133*1,103 = 1,563. Темп приросту Тt показує, на скільки відсотків рівень yt більше (менше) рівня взятого за базу порівняння. Його можна визначити як відношення абсолютного приросту до бази порівняння або безпосередньо на основі темпу зростання. Базисний темп приросту:
і т.ін. Ланцюговий темп приросту:
Темп нарощення – характеризує інтенсивність нарощення абсолютного приросту, та показує, який приріст припадає на одиницю виміру показника:
Абсолютне значення 1 % приросту показує, чого вартий 1 % і розраховується як співвідношення абсолютного приросту й темпу приросту. Алгебраїчно це співвідношення дорівнює 0,01 рівня, взятого за базу порівняння: А % = Dу / Тпр = yі – yі--1/ 100 (yі - y і-1/ yі-1) = yі-1 / 100 = 0,01 yі-1. А% = уi-1 / 100 = 0,01 уi-1. Для базисних темпів приросту значення А % однакові. Результати розрахунків оформлено в формі таблиці 3. Примітки: 1) Для тих, хто виконав зімкнення рядів необхідно виконати одну таблицю і докладні розрахунки до неї. 2) Для тих, хто має первинні дані в одну стрічку – теж має скласти одну таблицю і докладні розрахунки до неї. 3) Для тих, хто має вихідні дані у вигляді двох взаємопов’язаних показників (обсяг виробництво молока та поголів’я корів, обсяг виробництва та кількість робітників та інше), які розрахували на їх основі ще один показник (молочна продуктивність корів, продуктивність праці робітників та інше) складають 3 таблиці – по таблиці на кожний показник із докладними розрахунками тільки для першого показника. Таблиця 3.3 Розрахунок показників обсягів виробництва будівельної корпорації
де n - число періодів.
Поиск по сайту: |
 .
. .
.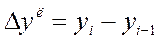 ,
, ,
, ,
, ,
, .
.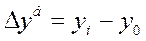 ,
, ,
, ,
, ,
,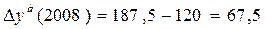 .
. .
. .
. = 112,5% ;
= 112,5% ; = 111,1% ;
= 111,1% ; = 113,3% ;
= 113,3% ; = 110,3% .
= 110,3% . .
. = 112,5% ;
= 112,5% ; = 125% ;
= 125% ;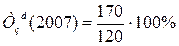 = 141,7% ;
= 141,7% ; = 156,3% .
= 156,3% . .
. .
. .
.
 .
. .
. = 12,5% ;
= 12,5% ;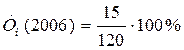 = 12,5% ;
= 12,5% ; = 16,7% ;
= 16,7% ; = 14,6% .
= 14,6% .

 або 111,8%.
або 111,8%.