 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи для самостоятельного решения. Кинематика гармонических колебаний.
КОЛЕБАНИЯ И ВОЛНЫ Кинематика гармонических колебаний. Сложение колебаний 1.1.1. Краткие теоретические сведения
В природе наблюдается тождественность законов, управляющих колебательными процессами различной природы. В связи с этим при решении задач следует обращать внимание на общие закономерности, которые присущи всем колебательным процессам. Для математического описания колебаний вводится параметр Система, движение которой есть гармоническое колебание, называется гармоническим осциллятором. Возмущение
где А – амплитуда колебания; Модуль мгновенной скорости возмущения определяется как производная от возмущения S(t), т. е.
Колебательная скорость Для поступательных колебаний Модуль мгновенного ускорения для возмущения Колебательное ускорение Для механических поступательных колебаний Величина
Фазовая точка с течением времени перемещается по фазовой траектории. Для гармонического осциллятора без затухания уравнение фазовой траектории можно найти, исключив параметр На фазовой плоскости гармоническое колебательное движение представляется окружностью с радиусом, равным амплитуде колебаний А (рис. 1.1.1).
Гармонические колебания удобно представлять в комплексной форме. При этом считается, что величина возмущения физической системы в любой момент времени представляется действительной частью комплексного возмущения Практическое удобство представления колебаний в комплексной форме состоит в том, что над комплексными величинами можно производить линейные операции (интегрирование, дифференцирование и др.), а затем использовать для дальнейших расчетов действительную часть полученной комплексной величины Используя комплексные числа, можно изменить фазу колебания осциллятора путем умножения возмущения 1) Изменение фазы колебаний на 2) Изменение фазы на 3) Изменение фазы на
Колебательное движение можно описывать, используя графическое представление колебаний. Гармоническое колебание (1.1.1) представляется как проекция вектора Для сложения колебаний, происходящих вдоль одной прямой, часто используют графический метод сложения векторов. Амплитуда результирующего колебания определяется по теореме косинусов (рис. 1.1.4):
Вектор
Вектор
где А и При сложении колебаний, происходящих по одному направлению, но с различными частотами
Если
Период изменения абсолютного значения амплитуды называется периодом биения; причем Если осциллятор участвует в двух взаимно перпендикулярных колебаниях, то уравнение движения результирующего колебания определяется путем исключения параметра t из системы двух уравнений.
Примеры решения задач ЗАДАЧА 1.Частица совершает гармонические колебания вдоль оси ОХ около положения равновесия х = 0. Частота колебаний
АНАЛИЗ. Для решения воспользуемся уравнениями кинематики гармонических колебаний. РЕШЕНИЕ. Закон движения частицы, совершающей гармонические колебания, определяется уравнением (1.1.1): За начало отсчета времени (t = 0) выберем момент, для которого заданы начальные условия: х0 = 25,0 см = 0,250 м,u0= 100 см/с = 1,00 м/с, колеблющейся частицы. Закон изменения скорости со временем найдем, продифференцировав по времени уравнение (1.1.6):
Уравнения (1.1.6) и (1.1.7) в точке t = 0 с учетом начальных условий имеют вид: x0= Acos Получили систему из двух уравнений для определения амплитуды А и начальной фазы
Уравнения (1.1.8) и (1.1.9) почленно возведем в квадрат и сложим:
Амплитуда колебаний А равна:
Правильность формулы по размерности очевидна. Разделив выражения (1.1.9) на (1.1.8), найдем тангенс начальной фазы колебаний: Учитывая, что a = 180° – 45° = 135° = 3p/4 = 2,35 рад. Подставив численные значения А и Найдем искомые значения координаты x1и скорости x1= 0,289 м,u1= 0,810 м/с. ОТВЕТ: x1= 0,289 м,u1 = 0,810 м/с.
ЗАДАЧА 2. Колебательный контур (рис. 1.1.5) состоит из конденсатора емкостью С = 0,025мкФ и катушки с индуктивностью L = 1,015Гн. Омическим сопротивлением цепи следует пренебречь. Конденсатор заряжен количеством электричества q0= 2,5×10–6 Кл. Написать для данного контура уравнения изменения: 1) разности потенциалов UC на обкладках конденсатора , 2) падения напряжения UL на катушке индуктивности, 3) силы тока в цепи в зависимости от времени. Найти сдвиг по фазе между напряжением UС на обкладках конденсатора и: а) током I в цепи, б) напряжением UL на катушке индуктивности. Найти уравнение фазовой траектории осциллятора.
АНАЛИЗ. В задаче рассматриваются незатухающие колебания в электрическом колебательном LC контуре при отсутствии омического сопротивления. с частотой
РЕШЕНИЕ. Заряд на обкладках конденсатора изменяется по закону (1.1.1): Сила тока в контуре
Напряжение на катушке индуктивности найдем, используя закон Фарадея и равенство (1.1.11):
Напряжение на обкладках конденсатора с учетом равенства (1.1.10) имеет вид:
Сравнение выражений для заряда (1.1.10) и напряжения UC (1.1.13) показывает, что эти величины изменяются в одной фазе. Закон изменения силы тока (1.1.11) можно представить в виде
Ток I в контуре опережает по фазе на
Сравнение уравнения (1.1.13) с (1.1.15) показывает, что напряжение на катушке индуктивности опережает по фазе на Определим численные коэффициенты в уравнениях (1.1.10), (1.1.13), (1.1.14), (1.1.15). Будем считать, что при t = 0заряд на обкладках конденсатора достигает максимального значения: q = A = q0 , тогда из равенства (1.1.10) получим Закон изменения разности потенциалов UC на обкладках конденсатора (1.1.13) с числовыми коэффициентами:
Закон изменения со временем силы тока I c числовыми коэффициентами получим из уравнения (1.1.14):
Закон изменения напряжения UL на катушке индуктивности получим из уравнения (1.1.15): UL = 2,5×10–6×1,015×6,282 ×106 cos(2 Напряжения UС на обкладках конденсатора и UL на катушке индуктивности изменяются в противофазе и имеют одинаковые амплитудные значения. Чтобы получить уравнение фазовой траектории колебательного контура, воспользуемся уравнением (1.1.10) и (1.1.11). Учтем, что колебательный импульс
Исключим параметр t из уравнений (1.1.10) и (1.1.16); учитывая, что
Равенства (1.1.17) и (1.1.18) возведем в квадрат и почленно сложим:
Таким образом, фазовая траектория осциллятора представляет собой окружность. ОТВЕТ:
ЗАДАЧА 3. Материальная точка участвует одновременно в двух колебательных процессах, происходящих в одном направлении по гармоническому закону с одинаковой частотой и амплитудами А1= 5см, А2= 10см и с разностью фаз
АНАЛИЗ. В задаче требуется сложить два гармонических колебаний, происходящих в одном направлении, и имеющих разные амплитуды и разность фаз. РЕШЕНИЕ. Обозначим смещение от общего положения равновесия для каждого из процессов согласно (1.1.1) соответственно: S1(t)= A1cos(w t + a1), (1.1.19) S2 (t)= A2cos(w t + a2). (1.1.20) Для простоты, начало отсчета в момент времени t0= 0 выберем так, чтобы S (t)= A1 cosw t + A2cos(w t+d). (1.1.21) Поскольку оба колебания – гармонические, имеющие одинаковую частоту wи одинаковое направление, результирующее колебание S (t)тоже является гармоническим и происходит с той же частотой w. Следовательно, закон движения (1.1.21) можно записать в виде S (t)= A cos(w t+a), (1.1.22) где А – амплитуда результирующего колебания, a – его начальная фаза. Сравнивая уравнения (1.1.21) и (1.1.22), получим: A cos(w t + a) = A1 cos(w t)+ A2cos(w t+d). (1.1.23) Уравнение (1.1.23) справедливо для любого момента времени и поэтому является тождеством. Задача состоит в определении неизвестных А и a. Ее можно решить различными методами: а) аналитическим методом, непосредственно решая это тождество; б) методом векторного сложения колебаний. Рассмотрим оба метода. В аналитическом методе используются формулы зависимости между тригонометрическими функциями двух углов. Воспользуемся зависимостью между тригонометрическими функциями двух углов: А cos(wt)×cosa – A sin(wt)×sina= А1cos(wt) + A2cos(wt)×cosd – A2 sin(wt)× sind. Полученное уравнение будет тождеством относительно переменной t, если коэффициенты при – A sina= A2sind, (1.1.24) Аcosa=А1 + А2cosd. (1.1.25) Чтобы найти амплитуду результирующего колебания, возведем (1.1.24) и (1.1.25) почленно в квадрат, а затем сложим: А2(sin2a + cos2a) = А22sin2d + A12+2A1A2cosd + A22cos2d, отсюда А2= A12 +А22+2A1A2cosd. Следовательно, Чтобы найти начальную фазу результирующего колебания, разделим (1.1.24) на (1.1.25): При расчете методом векторного сложения колебаний, последние представляются в виде векторов амплитуд Угол a наклона вектора Таким образом, результирующий колебательный процесс происходит с частотой wи описывается законом (1.1.22), где А и a определяются из равенств (1.1.26), (1.1.27) – соответственно, т. е. S(t)= 0,13cos(w t + 0,23p) , м. ОТВЕТ:
ЗАДАЧА 4. Точка одновременно участвует в n гармонических колебаниях одинаковой частоты w, направленных по одной прямой:
АНАЛИЗ. В задаче требуется сложить n гармонических колебаний, имеющих одинаковую частоту w. При решении необходимо использовать метод векторного сложения колебаний. РЕШЕНИЕ. Закон движения точки, участвующей в п колебаниях, имеет вид: S(t) = A cos (w t + a). (1.1.28) Начертим соответствующую векторную диаграмму, для определенности считая, что п = 4.
Из рис. 1.1.6. видно, что проекция Ax результирующего вектора
Проекция Ау результирующего колебания вектора
Амплитуда результирующего колебания А равна: Подставим (1.1.29) и (1.1.30) в окончательную формулу (1.1.31), учитывая при этом, что В результате получим Начальная фаза результирующего колебания определится из рис. 1.1.6:
ОТВЕТ: АНАЛИЗ. В задаче требуется сложить два гармонических колебания одного направления, имеющих разную круговую частоту w.
РЕШЕНИЕ. Амплитуда рассматриваемого колебания x = Acos2,1t×cos50,0t изменяется со временем по закону: При сложении колебаний, происходящих по одному направлению с различными частотами w1 и w2, возникает колебательное движение, называемое биением ( 2,1ТБ = p, При сложении колебаний разной частоты x1= A0cosw1t и x2= A0cosw2t, если их амплитуды равны, а
а его амплитуда согласно (1.1.4) имеет вид: Сравним эти выражения с уравнением биений x = Acos2,1t×cos50,0t. Получим А = 2А0,т. е.
Из системы уравнений (1.1.34) и (1.1.35) найдем значения частот w1= 47,9 с–1, w2= 52,1 с–1. Следовательно, биение x = A0cos2,1tcos50,0t с периодом ТБ= 1,5 свозникло в результате сложения колебаний с амплитудами ОТВЕТ: w1= 47,9 с–1, w2= 52,1 с–1; ТБ= 1,5 с. ЗАДАЧА 6. На вертикально отклоняющие пластины конденсатора подается напряжение
АНАЛИЗ. В задаче необходимо произвести сложение двух гармонических колебаний, происходящих во взаимно перпендикулярных плоскостях X и Y. Суммарное колебание будет одной из кривых Лиссажу, изображаемых на экране осциллографа. РЕШЕНИЕ. Уравнение колебаний для величины напряжения U на пластинах конденсатора в общем виде можно записать, учитывая (1.1.1): Ux = A1cos(w1 t + a1), Uy = A2 cos(w2t + a2). В данной задаче А1= 2В, т. е.
Амплитуда – величина существенно положительная и наличие знака «минус» в уравнении (1.1.37) определяется начальной фазой a2этого колебания. Воспользовавшись формулой приведения – cospt = cos(pt + p), получим Чтобы определить траекторию луча на экране осциллографа, необходимо из уравнений (1.1.36) и (1.1.37) исключить параметр t (время). Поскольку по условию задачи Подставим полученное выражение
или Уравнение (1.1.39) – это уравнение параболы, ось которой лежит на оси ОY. Амплитуда колебаний по оси OХ Uх = 2 В, по оси ОY – 1 В. Следовательно, абсциссы всех точек траектории заключены в пределах Для графического построения траектории воспользуемся уравнением (1.1.38) и найдем соответствующие координаты точек. Парабола на рис. 1.1.7. построена по найденным в табл. 1.1 координатам.
Таблица 1.1
В начальный момент времени ( ОТВЕТ:
ЗАДАЧА 7. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выраженных уравнениями
АНАЛИЗ. В задаче рассматривается сложение двух взаимно перпендикулярных колебаний, одно из которых опережает по фазе другое на величину РЕШЕНИЕ. Уравнения колебаний согласно условиям задачи имеют вид:
Колебание (1.1.41) опережает по фазе колебание (1.1.40) на Это каноническое уравнение эллипса с полуосями a = 2 см и Чтобы определить направление движения точки, учтем, что в момент
Скорость точки при ее движении по эллипсу равна Тогда
Модуль вектора ускорения:
В момент времени t = 0, численные значения скорости u= 3,14 см/c, ускорения – а = 19,7 см/с2. ОТВЕТ:
Задачи для самостоятельного решения 1. Точка колеблется по гармоническому закону 2. Найти зависимость скорости гармонического колебания от смещения. 3. Найти зависимость ускорения гармонического колебания 4. Определить зависимость ускорения гармонического колебания 5. Начальная фаза колебаний точки равна p/3. Период колебаний Т = 0,06 с. Определить ближайшие моменты времени, в которые скорость и ускорение в п = 2 раза меньше амплитудных значений. 6. Точка совершает колебания вдоль оси х по закону 7. Точка совершает гармонические колебания вдоль некоторой прямой с периодом Т = 0,60 с и амплитудой А = 10,0 см. Найти среднюю скорость точки за время, в течение которого она проходит путь А/2: а) из крайнего положения, б) из положения равновесия. 8. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 2,4 см, скорость точки равна 3 см/с, а при смещении, равном 2,8 см, скорость равна 2 см/с. Найти амплитуду и период этого колебания. 9. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/с, период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм. 10. Материальная точка совершает гармонические колебания с частотой n = 500 Гц и амплитудой А = 0,02 см. Определить среднее значение скорости 11. За какую часть периода точка, совершающая гармонические колебания, пройдет путь, равный: 1) половине амплитуды, если в начальный момент времени она находилась в положении равновесия; 2) одной трети амплитуды, если в начальный момент времени она находилась в крайнем положении? 12. При сложении двух одинаково направленных гармонических колебаний с одной и той же частотой и амплитудами, равными 2 см и 4 см, получается гармоническое колебание с амплитудой 5 см. Найти разность фаз складываемых колебаний. 13. Точка участвует в трех колебаниях, происходящих по одной прямой и выраженных уравнениями: 14. Точка участвует одновременно в двух колебаниях одного направления, которые происходят по законам 15. Найти графически амплитуду А колебаний, которые возникают при сложении следующих колебаний одного направления: а) 16. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями 17. “Зайчик” колеблется гармонически с некоторой неизменной частотой относительно шкалы, которая, в свою очередь, совершает гармонические колебания по отношению к стенке. Оба колебания происходят вдоль одного и того же направления. При частотах колебаний шкалы n1 = 20 Гц и n2 = 22 Гц частота биений “зайчика” относительно стенки оказывается одинаковой. При какой частоте n¢ колебаний частота биений “зайчика” станет вдвое больше? 18. Точка движется в плоскости XY по закону 19. Найти уравнение траектории 20. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях: 21. На вертикально и горизонтально отклоняющиеся пластины осциллографа поданы напряжения 22. На вертикально и горизонтально отклоняющиеся пластины осциллографа подаются напряжения 23. На вертикально отклоняющиеся пластины осциллографа подаются два одинаково направленных колебания 24. Колебательный контур состоит из конденсатора емкостью С = 5 мкФ и катушки индуктивностью L = 0,200 Гн. Определить максимальную силу тока 25. Катушка, индуктивность которой L = 3×10–5 Гн, присоединена к плоскому конденсатору с площадью пластин 26. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре дано в виде 27. Уравнение изменения тока в колебательном контуре со временем имеет вид:
Поиск по сайту: |
 , характеризующий состояние колеблющейся системы и называемый смещением (возмущением). Для поступательных механических колебаний смещение
, характеризующий состояние колеблющейся системы и называемый смещением (возмущением). Для поступательных механических колебаний смещение  – линейное отклонение от положения равновесия; для электрических колебаний
– линейное отклонение от положения равновесия; для электрических колебаний 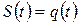 – отклонение величины заряда; для тел, совершающих вращательное движение, крутильные колебания
– отклонение величины заряда; для тел, совершающих вращательное движение, крутильные колебания 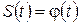 – угол отклонения от положения равновесия и др. В зависимости от природы колебаний смещение
– угол отклонения от положения равновесия и др. В зависимости от природы колебаний смещение  ,
,  , (1.1.1)
, (1.1.1) – фаза колебания; a–начальная фаза колебаний; w – циклическая частота колебаний, равная
– фаза колебания; a–начальная фаза колебаний; w – циклическая частота колебаний, равная  (Т – период колебаний).
(Т – период колебаний). . Если
. Если  и
и  , то
, то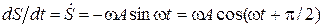 .
. опережает по фазе возмущение
опережает по фазе возмущение 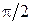 .
. – колебательная скорость совпадает с обычной механической скоростью; для крутильных колебаний
– колебательная скорость совпадает с обычной механической скоростью; для крутильных колебаний  – угловая скорость движения; для электрических колебаний
– угловая скорость движения; для электрических колебаний  – сила тока.
– сила тока. .
. опережает по фазе возмущение
опережает по фазе возмущение  – обычное механическое ускорение; для крутильных колебаний
– обычное механическое ускорение; для крутильных колебаний  – угловое ускорение; для электрических колебаний
– угловое ускорение; для электрических колебаний  , где UL – напряжение на катушке индуктивности колебательного контура.
, где UL – напряжение на катушке индуктивности колебательного контура. называется колебательным импульсом осциллятора. Плоскость, на которой по оси абсцисс откладывается величина возмущения
называется колебательным импульсом осциллятора. Плоскость, на которой по оси абсцисс откладывается величина возмущения  Рис. 1.1.1.
Рис. 1.1.1.
 из уравнений:
из уравнений:  ,
,  Уравнение фазовой траектории имеет вид:
Уравнение фазовой траектории имеет вид: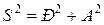 .
. Рис. 1.1.2.
Рис. 1.1.2.
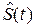 , т. к.
, т. к. 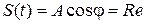
 , где
, где  . Колебания можно представить в комплексной форме, воспользовавшись формулой Эйлера:
. Колебания можно представить в комплексной форме, воспользовавшись формулой Эйлера:  , где
, где  ,
, 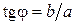 (см. рис. 1.1.2).
(см. рис. 1.1.2). на соответствующее число:
на соответствующее число: соответствует умножению
соответствует умножению  соответствует умножению
соответствует умножению 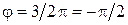 соответствует умножению
соответствует умножению  Рис. 1.1.3.
Рис. 1.1.3.
 , вращающегося против часовой стрелки с угловой скоростью w(рис. 1.1.3). Вектор
, вращающегося против часовой стрелки с угловой скоростью w(рис. 1.1.3). Вектор  , равным начальной фазе колебаний. Модуль вектора
, равным начальной фазе колебаний. Модуль вектора  . В результате проекция
. В результате проекция 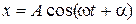 , что соответствует уравнению колебательного движения (1.1.1)
, что соответствует уравнению колебательного движения (1.1.1) . (1.1.2)
. (1.1.2) Рис. 1.1.4.
Рис. 1.1.4.
 , который определяет начальную фазу результирующего колебания. Из рис. 1.1.4 видно, что
, который определяет начальную фазу результирующего колебания. Из рис. 1.1.4 видно, что . (1.1.3)
. (1.1.3) ,и результирующее колебание имеет вид:
,и результирующее колебание имеет вид: и
и  , используя аналогичные рассуждения, можно получить, что амплитуда результирующего колебания А изменяется со временем по закону
, используя аналогичные рассуждения, можно получить, что амплитуда результирующего колебания А изменяется со временем по закону . (1.1.4)
. (1.1.4) , а А01= А02= А0, такое колебательное движение называется биением и описывается уравнением:
, а А01= А02= А0, такое колебательное движение называется биением и описывается уравнением: . (1.1.5)
. (1.1.5) .
. . (1.1.6)
. (1.1.6) . (1.1.7)
. (1.1.7) , (1.1.8)
, (1.1.8) . (1.1.9)
. (1.1.9) .
. м.
м. .
. ,определим начальную фазу
,определим начальную фазу  , м;
, м;  , м/с.
, м/с. в момент времени t1= 2,40 c:
в момент времени t1= 2,40 c:




 – ?
– ?
 .
. Рис. 1.1.5
Рис. 1.1.5
 . (1.1.10)
. (1.1.10) . (1.1.11)
. (1.1.11) . (1.1.12)
. (1.1.12) . (1.1.13)
. (1.1.13) . (1.1.14)
. (1.1.14) напряжение UC на обкладках конденсатора. Закон изменения напряжения UL на катушке индуктивности получим из уравнения (1.1.12):
напряжение UC на обкладках конденсатора. Закон изменения напряжения UL на катушке индуктивности получим из уравнения (1.1.12): . (1.1.15)
. (1.1.15) напряжение на обкладках конденсатора.
напряжение на обкладках конденсатора. t, где
t, где  рад/c.
рад/c. , В.
, В.
 , A.
, A. ×103t+
×103t+ 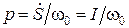 , тогда:
, тогда: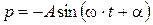 . (1.1.16)
. (1.1.16) , (1.1.17)
, (1.1.17) . (1.1.18)
. (1.1.18) .
. , В;
, В;  , В;
, В;  , A; уравнение фазовой траектории
, A; уравнение фазовой траектории  .
.
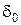 – ?
– ?
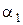 = 0, тогда
= 0, тогда  . Закон движения точки, участвующий в двух колебательных процессах, определится согласно принципу суперпозиции и уравнениям движения (1.1.19) и (1.1.20):
. Закон движения точки, участвующий в двух колебательных процессах, определится согласно принципу суперпозиции и уравнениям движения (1.1.19) и (1.1.20): и sin
и sin  в левой его части соответственно равны коэффициентам в правой части:
в левой его части соответственно равны коэффициентам в правой части: м. (1.1.26)
м. (1.1.26)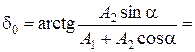 41° = 0,23p. (1.1.27)
41° = 0,23p. (1.1.27) и
и  , которые вращаются с угловой скоростью w против часовой стрелки (см. рис. 1.1.4). Вектор
, которые вращаются с угловой скоростью w против часовой стрелки (см. рис. 1.1.4). Вектор  . Векторное сложение позволяет учесть различие в фазах колебаний (1.1.19) и (1.1.20). Из рис. 1.1.4 следует, что в данной задаче модуль вектора А проще найти, используя теорему косинусов:
. Векторное сложение позволяет учесть различие в фазах колебаний (1.1.19) и (1.1.20). Из рис. 1.1.4 следует, что в данной задаче модуль вектора А проще найти, используя теорему косинусов:  , т. е.
, т. е.  м, что согласуется с результатом (1.1.26).
м, что согласуется с результатом (1.1.26). 41°, что также согласуется с полученным выше результатом (1.1.27).
41°, что также согласуется с полученным выше результатом (1.1.27). м;
м;  .
. ;
;  ;
;  ;...
;... . Определить амплитуду и начальную фазу результирующего колебания.
. Определить амплитуду и начальную фазу результирующего колебания. i = 1, 2, 3, ... n
i = 1, 2, 3, ... n
 Рис. 1.1.6
Рис. 1.1.6
 отдельных колебаний:
отдельных колебаний: . (1.1.29)
. (1.1.29) на ось OY определяется как
на ось OY определяется как . (1.1.30)
. (1.1.30) . (1.1.31)
. (1.1.31) , а
, а 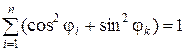 .
. .
. .
.
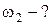 ТБ – ?
ТБ – ?
 ;
;  . ЗАДАЧА 5. При сложении двух гармонических колебаний одного направления результирующее колебание имеет вид: x = Acos2,1tcos50,0t, м, где t измеряется в секундах. Найти частоты складываемых колебаний и период биений.
. ЗАДАЧА 5. При сложении двух гармонических колебаний одного направления результирующее колебание имеет вид: x = Acos2,1tcos50,0t, м, где t измеряется в секундах. Найти частоты складываемых колебаний и период биений. . (1.1.32)
. (1.1.32)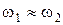 ). Частота пульсаций амплитуды называется частотой биений. Амплитуда – величина существенно положительная. Следовательно, период биений равен промежутку времени, за который аргумент косинуса изменяется на p, т. е. согласно (1.1.32):
). Частота пульсаций амплитуды называется частотой биений. Амплитуда – величина существенно положительная. Следовательно, период биений равен промежутку времени, за который аргумент косинуса изменяется на p, т. е. согласно (1.1.32):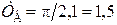 с. (1.1.33)
с. (1.1.33) ,
, .
. ,
, , (1.1.34)
, (1.1.34)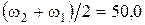 . (1.1.35)
. (1.1.35) , и частотами w1= 47,9 рад/с, w2= 52,1 рад/с. Их уравнения с числовыми коэффициентами имеют вид:
, и частотами w1= 47,9 рад/с, w2= 52,1 рад/с. Их уравнения с числовыми коэффициентами имеют вид: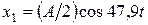 ;
;  .
. , на горизонтально отклоняющие – напряжение
, на горизонтально отклоняющие – напряжение  . Определить траекторию луча на экране осциллографа.
. Определить траекторию луча на экране осциллографа.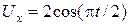 , В
, В
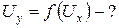
 рад/с, А2= 1В,
рад/с, А2= 1В, 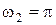 рад/с,
рад/с,  ,
, . Уравнения колебаний с числовыми коэффициентами имеют вид:
. Уравнения колебаний с числовыми коэффициентами имеют вид: (1.1.36)
(1.1.36) . (1.1.37)
. (1.1.37) . Полученное значение подставим в уравнение (1.1.36), найдем
. Полученное значение подставим в уравнение (1.1.36), найдем  , отсюда
, отсюда  ,
,  .
. в уравнение (1.1.37):
в уравнение (1.1.37): , (1.1.38)
, (1.1.38) Рис. 1.1.7
Рис. 1.1.7
 . (1.1.39)
. (1.1.39) , а ординаты
, а ординаты  .
.
 ) напряжение на горизонтально и вертикально отклоняющих пластинах конденсатора равно
) напряжение на горизонтально и вертикально отклоняющих пластинах конденсатора равно  В,
В,  В (точка А на графике). Точка начинает колебание из положения А и за время
В (точка А на графике). Точка начинает колебание из положения А и за время  с совершит полное колебание по оси
с совершит полное колебание по оси  ОY, когда дойдет до точки С. Затем она начнет двигаться в обратном направлении. Полное колебание по оси ОY точка совершит за время
ОY, когда дойдет до точки С. Затем она начнет двигаться в обратном направлении. Полное колебание по оси ОY точка совершит за время  с и вновь вернется в точку А. Когда точка совершит одно полное колебание по оси ОY, она совершит половину полного колебания по оси ОX, т. к.
с и вновь вернется в точку А. Когда точка совершит одно полное колебание по оси ОY, она совершит половину полного колебания по оси ОX, т. к.  с, Т2 = 2 с.
с, Т2 = 2 с. .
. ,
,  (смещения даны в см). Найти уравнение траектории точки. Показать на чертеже направление движения точки. Определить скорость и ускорение точки в момент
(смещения даны в см). Найти уравнение траектории точки. Показать на чертеже направление движения точки. Определить скорость и ускорение точки в момент  , см
t = 0,5 с
, см
t = 0,5 с



 . Исключив из уравнений (1.1.40) и (1.1.41)параметр t, получим уравнение траектории:
. Исключив из уравнений (1.1.40) и (1.1.41)параметр t, получим уравнение траектории:  .
. см (уравнение 1.1.41). Следовательно, точка находится в положении А. При возрастании t увеличивается x, а
см (уравнение 1.1.41). Следовательно, точка находится в положении А. При возрастании t увеличивается x, а  Рис.1.1.8
Рис.1.1.8
 . Модуль скорости для взаимно перпендикулярных колебаний:
. Модуль скорости для взаимно перпендикулярных колебаний:  ; аналогично для модуля вектора ускорения получим
; аналогично для модуля вектора ускорения получим  . Учитывая (1.1.40) и (1.1.41), найдем:
. Учитывая (1.1.40) и (1.1.41), найдем:  ,
,  (уравнение 1.1.5).
(уравнение 1.1.5). ,
,  . Модуль вектора скорости:
. Модуль вектора скорости: .
. .
. ; u= 3,14 см/c; а = 19,7 см/с2.
; u= 3,14 см/c; а = 19,7 см/с2.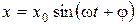 . Найти максимальные значения скорости и ускорения.
. Найти максимальные значения скорости и ускорения.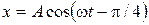 . Построить графики смещения х, проекции скорости
. Построить графики смещения х, проекции скорости  и проекции ускорения
и проекции ускорения 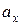 как функции времени
как функции времени  .
.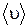 и ускорения
и ускорения  точки на пути от ее крайнего положения до положения равновесия, найти максимальные значения этих величин.
точки на пути от ее крайнего положения до положения равновесия, найти максимальные значения этих величин. ,
,  ,
,  (смещения даны в см). Определить амплитуду и начальную фазу результирующего колебания. Написать его уравнение движения.
(смещения даны в см). Определить амплитуду и начальную фазу результирующего колебания. Написать его уравнение движения. и
и  . Найти максимальную скорость точки.
. Найти максимальную скорость точки. ,
,  ; б)
; б)  ,
,  ,
,  .
.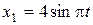 ,
,  , см. Написать уравнение результирующего колебания. Начертить векторную диаграмму сложения амплитуд.
, см. Написать уравнение результирующего колебания. Начертить векторную диаграмму сложения амплитуд. ,
,  ,где А, В,
,где А, В,  точки и направление ее движения по этой траектории; б) ускорение
точки и направление ее движения по этой траектории; б) ускорение  точки в зависимости от ее радиус-вектора
точки в зависимости от ее радиус-вектора  относительно начала координат.
относительно начала координат. точки, если она движется по закону: а)
точки, если она движется по закону: а)  ,
,  ; б)
; б)  .
. и
и  . Найти траекторию движения точки и вычертить ее с нанесением масштаба.
. Найти траекторию движения точки и вычертить ее с нанесением масштаба. и
и 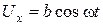 . Определить траекторию луча на экране.
. Определить траекторию луча на экране. . Определить траекторию луча на экране.
. Определить траекторию луча на экране.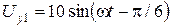 и
и  , на горизонтально отклоняющиеся пластины
, на горизонтально отклоняющиеся пластины  . Определить траекторию луча на экране осциллографа.
. Определить траекторию луча на экране осциллографа.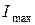 в контуре, если максимальная разность потенциалов на обкладках конденсатора
в контуре, если максимальная разность потенциалов на обкладках конденсатора  В. Омическим сопротивлением
В. Омическим сопротивлением  контура пренебречь.
контура пренебречь. см2 и расстоянием между ними
см2 и расстоянием между ними 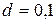 мм. Чему равна диэлектрическая проницаемость среды, заполняющей пространство между пластинами, если собственной частоте контура соответствует длина волны 750 м?
мм. Чему равна диэлектрическая проницаемость среды, заполняющей пространство между пластинами, если собственной частоте контура соответствует длина волны 750 м? , В. Емкость конденсатора равна 10–9 Ф. Найти: 1) период колебаний в контуре; 2)индуктивность контура; 3) закон изменения со временем силы тока в цепи.
, В. Емкость конденсатора равна 10–9 Ф. Найти: 1) период колебаний в контуре; 2)индуктивность контура; 3) закон изменения со временем силы тока в цепи. , А. Индуктивность контура 1 Гн. Найти: 1) период колебаний; 2) емкость контура; 3) максимальную разность потенциалов на обкладках конденсатора.
, А. Индуктивность контура 1 Гн. Найти: 1) период колебаний; 2) емкость контура; 3) максимальную разность потенциалов на обкладках конденсатора.