 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производные и дифференциалы высших порядков ⇐ ПредыдущаяСтр 4 из 4
В математике широко используются производные функции высших порядков. Это оправдывается хотя бы тем, что физический смысл второй производной представляет собой ускорение тела. В самом деле, если вторую производную функции ввести как производную от производной, то есть
и учесть, что физический смысл первой производной есть скорость, то вторая производная, очевидно, показывает скорость изменения этой скорости, то есть ускорение. Аналогично можно ввести понятия третьей, четвертой и так далее производных: За редким исключением производные высших порядков вычисляются последовательно, то есть для получения пятой производной необходимо вначале найти первую, затем вторую, третью и четвертую производные, и после этого пятую производную. Пример 1.
На примере 1 было показано, как находить старшие производные для явнозаданной функции. Пример 2. Вычислим вторую производную неявной функции
Определим вначале первую производную, дифференцируя обе части равенства по
Дифференцируем полученное уравнение еще раз
тогда
После приведения подобных членов
определяем
Из полученного выражения можно исключить первую производную, которую определим из ранее полученного уравнения
Примеры для самостоятельного решения
Вычислить 7.24. Определим вторую производную для параметрическизаданной функции, для чего выведем необходимую для этого формулу. Ранее была получена формула для первой производной функции
Итак,
Пример. Дана функция В соответствии с полученной формулой находим
Очевидно,
Примеры для самостоятельного решения
Вычислить 7.26.
Дифференциалы высших порядков
По аналогии с производными введем понятие дифференциала второго порядка, обозначив его
Этот дифференциал не обладает инвариантностью формы записи. Покажем это. Очевидно,
Если функция
Когда функция сложная
Еще больше дополнительных членов появляется в третьем дифференциале сложной функции и так далее. § 7.8. Формула Тейлора
Рассмотрим полученную ранее формулу для приращения дифференцируемой функции
Таким образом, функцию Пусть
где
……………………………….
Подсчитаем вычисленные производные при
Подставляем полученные коэффициенты в формулу, в результате
Проанализируем, что следует из условий, налагаемых на остаточный член. Из условия
следовательно, при
Такое представление остаточного члена показывает, что остаточный член есть бесконечно малая, более высокого порядка малости, чем Полученная формула используется для приближенного вычисления значения функции с помощью полинома. Имеется несколько вариантов остаточных членов, более приспособленных для установления количества сохраняемых в формуле членов, обеспечивающих наперед заданную точность приближенного вычисления (аппроксимации) функции. Сведения о них имеются в литературе, указанной в списке. Широко используется частный случай формулы Тейлора – формула Маклорена
представляющая разложение функции в окрестности нулевой точки.
Пример 1. Рассмотрим функцию
Пример 2. Рассмотрим функцию Тогда
Первые члены формулаы Маклорена принимают вид
Поиск по сайту: |
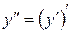 ,
, ,
, 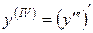 …..
…..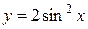 ,
, 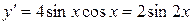 ,
, 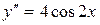 ,
, 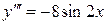 …
…
 ,
, 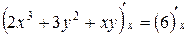 или
или .
. ,
, .
.
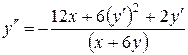 .
.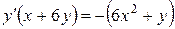 тогда
тогда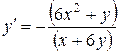 .
.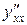
 , 7.25.
, 7.25. 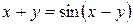 .
.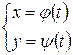 , которая имела вид
, которая имела вид 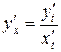 . Дифференцируем обе части равенства по
. Дифференцируем обе части равенства по 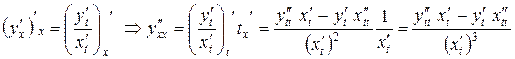 .
. .
.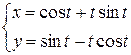 . Определить
. Определить  ,
,  ,
, ,
,  ,
,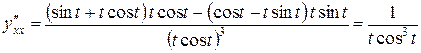 .
. , 7.27.
, 7.27.  , 7.28.
, 7.28. 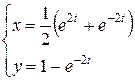 .
.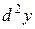 :
: .
.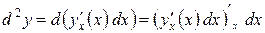 .
. простая, то есть,
простая, то есть,  независимая переменная, то аргумент
независимая переменная, то аргумент 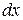 никак не связаны между собой, другими словами
никак не связаны между собой, другими словами  .
. , имеется связь между ее промежуточным аргументом
, имеется связь между ее промежуточным аргументом  и его приращением
и его приращением 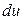 поскольку и
поскольку и  . В выражении для производной, а следовательно, и дифференциала появляется второе слагаемое
. В выражении для производной, а следовательно, и дифференциала появляется второе слагаемое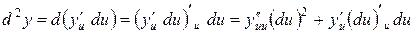 .
.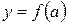 . Для точек
. Для точек 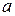 и
и 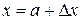 она примет вид
она примет вид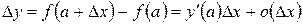 , в этом случае
, в этом случае 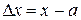 и формулу можно привести к виду
и формулу можно привести к виду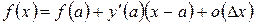 .
. приближенно с погрешностью
приближенно с погрешностью 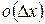 можно представить в виде линейной относительно
можно представить в виде линейной относительно  , вносимая погрешность является бесконечно малой более высокого порядка малости по сравнению с
, вносимая погрешность является бесконечно малой более высокого порядка малости по сравнению с 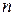 раз дифференцируемая функция, то есть имеющая
раз дифференцируемая функция, то есть имеющая 
 ,
,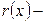 остаточный член, показывающий отличие
остаточный член, показывающий отличие  ой степени в правой части формулы. Определяем коэффициенты этого многочлена. Полагаем
ой степени в правой части формулы. Определяем коэффициенты этого многочлена. Полагаем 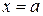 . Тогда
. Тогда 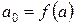 при выполнении условия
при выполнении условия 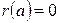 . Дифференцируем эту функцию поочередно
. Дифференцируем эту функцию поочередно 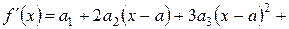
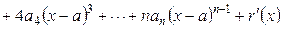 ,
,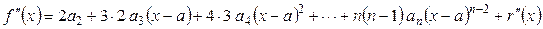 ,
,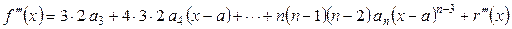 ,
,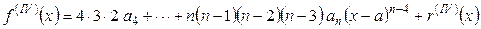 ,
,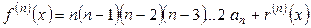 .
.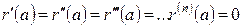 из формулы для первой производной имеем
из формулы для первой производной имеем 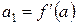 , из формулы для второй производной следует
, из формулы для второй производной следует  , формула для третьей и четвертой производных приводит к
, формула для третьей и четвертой производных приводит к ,
,  ,…
,… 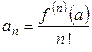 .
.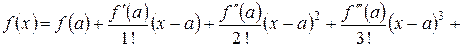
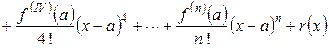 .
.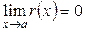 , то есть
, то есть 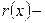 бесконечно малая при
бесконечно малая при 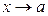 . Поскольку
. Поскольку  , где
, где 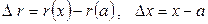 ,
,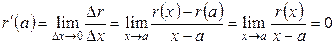 ,
, . Совершая аналогичную процедуру с остальными условиями на производные остаточного члена, выясняем, что в вышеприведенной формуле остаточный член при
. Совершая аналогичную процедуру с остальными условиями на производные остаточного члена, выясняем, что в вышеприведенной формуле остаточный член при  . Тогда
. Тогда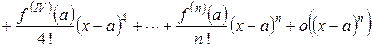 .
. ,
, . Нетрудно заметить, что любая производная этой функции равна самой функции, а
. Нетрудно заметить, что любая производная этой функции равна самой функции, а  . В соответствии с формулой Маклорена
. В соответствии с формулой Маклорена .
.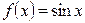 . Очевидно,
. Очевидно, 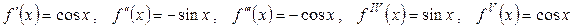 и т.д.
и т.д.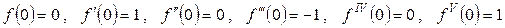 и так далее.
и так далее.