 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Схема вычисления производной
Производная Пусть функция y = f (x) определена на промежутке X. Возьмем точку Определение. Производной функции y = f (x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует)
Нахождение производной функции называется дифференцированием этой функции. Если функция в точке x имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке. Геометрический смысл производной: производная Тогда уравнение касательной к кривой y = f (x) в точке
Механический смысл производной: производная пути по времени
Экономический смысл производной: производная объема произведенной продукции по времени
Зависимость между непрерывностью и Теорема. Если функция y = f (x) дифференцируема в точке Обратная теорема неверна, то есть если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке. Примером может служить функция y = |x|, непрерывная в точке x = 0, но имеющая в ней «излом». Производная этой функции в точке x = 0 не существует, так как Таким образом, непрерывность функции – необходимое, но недостаточное условие дифференцируемости функции.
Схема вычисления производной Производная функции 1. Дадим аргументу x приращение 2. Находим приращение функции 3. Составляем отношение 4. Находим предел этого отношения при
Пример 1. Найти производную функции Решение: 1. Дадим аргументу x приращение 2. Находим приращение функции:
3. Составляем отношение 4. Находим предел Ответ:
Правила дифференцирования: 1. Производная постоянной равна нулю: 2. Производная аргумента равна единице: 3. Производная суммы равна сумме производных этих функций
4. Производная произведения двух дифференцируемых функций равна:
5. Постоянный множитель можно выносить за знак производной
6. Производная частного двух дифференцируемых функций может быть найдена по формуле:
7. Производная сложной функции равна
Производные основных элементарных функций: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. Пример 2. Вычислить Решение: Находим производную суммы
Пример 3. Вычислить Решение: Находим производную произведения
Пример 4. Вычислить Решение: Находим производную частного
Пример 5. Вычислить Решение: Находим производную сложной функции
Поиск по сайту: |
 . Дадим значению x приращение
. Дадим значению x приращение  , тогда функция получит приращение
, тогда функция получит приращение  .
. .
.
 есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой y = f (x) в точке
есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой y = f (x) в точке  , то есть
, то есть  .
. .
. есть скорость точки в момент
есть скорость точки в момент 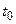 :
: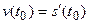 .
.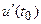 есть производительность труда в момент
есть производительность труда в момент  :
: 

 может быть найдена по следующей схеме:
может быть найдена по следующей схеме: .
. .
. , то есть
, то есть  (если этот предел существует).
(если этот предел существует). .
.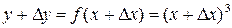 .
.
 .
. .
.
 .
. .
. .
. .
. .
. , где
, где  .
. , где
, где  .
. .
. , где
, где 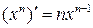 ;
; ;
;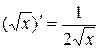 ;
; ;
; при
при  ;
; ;
; ;
; ,
,  ;
;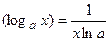 ;
; ;
; ;
; , если
, если  .
. .
. .
. .
. .
. .
. .
. .
.