 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сопряженный линейный операторСтр 1 из 5Следующая ⇒
ГЛАВА 7. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ §1. Некоторые сведения о матрицах Ортогональные и унитарные матрицы
Определение. Комплексная квадратная матрица А называется унитарной, если Следствия. 1. Модуль определителя унитарной матрицы равен 1. ►Из определения следует: 2. В силу равносильности любое из этих равенств может служить определением унитарной матрицы. Определение. Действительная квадратная матрица Следствия. 1. 2. Определитель ортогональной матрицы равен 1 или –1. 3. Каждое из этих равенств опять же может служить определением ортогональной матрицы.
Свойства ортогональных и унитарных матриц
1º. 2º. 3º. ►Докажем, например, первое свойство для унитарных матриц (для ортогональных доказательство отличается только тем, что отсутствует комплексное сопряжение).
Теорема 7.1 о матрице перехода. Пусть в евклидовом пространстве и ещё какой-либо базис Для того чтобы базис (7.2) был ортонормированным, необходимо и достаточно, чтобы матрица Т перехода от (7.1) к (7.2) была унитарной для комплексного евклидова пространства, и ортогональной для действительного. ►Доказательство проводим для комплексного случая. Если {(7.2) – ортонормированный}
Некоторые свойства эрмитовых и симметричных матриц
Вспомним, что комплексная квадратная матрица А называется эрмитовой, если
1º. 2º 3º.
Сопряженный линейный оператор Лемма. 7.1.Пусть ►
Определение. Линейный оператор
Теорема 7.2.Для любого линейного оператора ►Доказываем теорему так же, как в свое время доказывали аналогичную теорему для обратного линейного оператора. Все доказательства проводим для комплексного пространства. Для действительного доказательство изменится только тем, что не будет комплексного сопряжения. Единственность. Предположим, что некоторый линейный оператор
то на основании доказанной леммы 7.1 Существование. Выберем в
и обозначим А матрицу оператора
Таким образом, Упражнение. Пусть оператор
Поиск по сайту: |
 . Множество всех унитарных матриц n-го порядка будем обозначать
. Множество всех унитарных матриц n-го порядка будем обозначать  .
. , значит,
, значит,  .◄
.◄ .
. называется ортогональной, если
называется ортогональной, если  . Множество всех ортогональных матриц n-го порядка будем обозначать
. Множество всех ортогональных матриц n-го порядка будем обозначать  .
. .
. .
. . 1'.
. 1'.  .
. . 2'.
. 2'.  .
. . 3'.
. 3'.  .
. .◄
.◄ заданы: ортонормированный базис
заданы: ортонормированный базис (7.1)
(7.1) . (7.2)
. (7.2) и
и  – матрицы Грама базисов (7.1) и (7.2) соответственно, то
– матрицы Грама базисов (7.1) и (7.2) соответственно, то  и
и  . Тогда
. Тогда .◄
.◄ , а действительная квадратная матрица А – симметричной, если
, а действительная квадратная матрица А – симметричной, если  . Будем обозначать
. Будем обозначать  – множество всех эрмитовых матриц n-го порядка, а
– множество всех эрмитовых матриц n-го порядка, а  – множество всех действительных симметричных матриц n-го порядка. Очевидно,
– множество всех действительных симметричных матриц n-го порядка. Очевидно,  . Запишем некоторые свойства этих матриц, которые вы можете легко доказать в качестве упражнения.
. Запишем некоторые свойства этих матриц, которые вы можете легко доказать в качестве упражнения. . 1'.
. 1'.  .
. . 2'.
. 2'.  .
.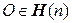 . 3'.
. 3'.  .
. и
и  – линейные операторы. Если для всех векторов евклидова пространства
– линейные операторы. Если для всех векторов евклидова пространства  выполняется одно из условий
выполняется одно из условий  или
или  , то
, то  .
.



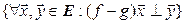

 (объясните каждый шаг в цепочке рассуждений). Второе утверждение доказывается аналогично.◄
(объясните каждый шаг в цепочке рассуждений). Второе утверждение доказывается аналогично.◄ называется сопряженным линейному оператору
называется сопряженным линейному оператору  .
. существует единственный сопряженный ему оператор
существует единственный сопряженный ему оператор  . При этом если А – матрица оператора
. При этом если А – матрица оператора  в некотором ортонормированном базисе пространства
в некотором ортонормированном базисе пространства  , то матрица оператора
, то матрица оператора  в том же базисе совпадает с матрицей
в том же базисе совпадает с матрицей  .
. . Так как
. Так как 
 и
и  ,
, (7.3)
(7.3) и обозначим
и обозначим  и
и  соответственно их координатные столбцы в базисе (7.3). В том же базисе координатные столбцы векторов
соответственно их координатные столбцы в базисе (7.3). В том же базисе координатные столбцы векторов  и
и  совпадают соответственно со столбцами
совпадают соответственно со столбцами  и
и  . На основании правила вычисления скалярного произведения в ортонормированном базисе получаем
. На основании правила вычисления скалярного произведения в ортонормированном базисе получаем .
. и
и  соответственно. Докажите: если матрица линейного оператора
соответственно. Докажите: если матрица линейного оператора  в первом из этих базисов совпадает с
в первом из этих базисов совпадает с  , то во втором матрица этого оператора совпадает с
, то во втором матрица этого оператора совпадает с  .
.