 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Примеры исследования функций с помощью производных и построение графиков
Пример 1.Исследовать функцию у = Решение. 1) Функция у = 2) x=1 – точка разрыва функции. Исследуем поведение функции в граничных точках области определения:
3) Найдем точки пересечения графика функции с осями координат. При х = 0 получаем у = 0, т.е. график функции пересекает координатные оси в точке O(0,0). 4) Прямая х = 1 является вертикальной асимптотой графика функции. Найдем наклонные асимптоты: k= b = т.е. b=2. Имеем уравнение правой наклонной асимптоты y = x+2. Легко убедиться, что при x ®–¥ k и b имеют те же значения, т.е. уравнение левой наклонной асимптоты такое же y = x+2. 5) Найдем производную функции: y' = = Приравнивая y' к нулю, получим x3–3x2=0, откуда имеем критические точки x1=0, x2=3. Для исследования знака производной в интервале (–¥;0), (0;3) и (3; +¥) на числовой оси отметим точки x=0, x=3 и х=1.
Таким образом, в интервале (–¥;1) функция возрастает, в интервале (1,3) – убывает, в интервале (3,+ ¥) она возрастает. В точке x=3 функция имеет минимум: f (3) = 6) Найдем вторую производную: y''= = Точка x=0 является точкой перегиба. При x<0 кривая направлена выпуклостью вверх, так как y''<0, а при x>0 – выпуклостью вниз. В точке перегиба f (x) имеет значение f (0)=0. Результаты наших исследований объединим в таблицу.
Строим график функции, предварительно построив асимптоты и отметив точки минимума, перегиба и пересечения графика с осями координат.
Пример 2. Исследовать функцию 1. Область определения: 2. Пусть Найдена точка 3. 4. Функция непрерывна во всей области определения. Вертикальных асимптот нет. 5. Невертикальные асимптоты.
6.
+ - +
На интервалах
7.
На интервале 8.
Поиск по сайту: |
 и построить ее график.
и построить ее график. определена всюду, кроме точки x=1. Отсюда область определения её: (–¥,1) È(1,+¥) .
определена всюду, кроме точки x=1. Отсюда область определения её: (–¥,1) È(1,+¥) . f (x) =
f (x) =  = +¥,
= +¥, f (x) =
f (x) = 
 =
=  =+¥;
=+¥;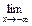
 =
=  =
=  =
=  =
=  = 1, т.е. k =1;
= 1, т.е. k =1; =
=  = =
= =  =
=  =
= 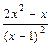 = =
= =  =
=  =2,
=2, =
=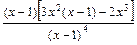 =
=  =
= 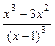 .
. Определим знаки y' =
Определим знаки y' =  в указанных интервалах.
в указанных интервалах.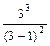 =
=  = 6,75.
= 6,75.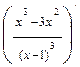 =
=  = =
= =  =
= =
=  , y''=0 при x=0. Так как знаменатель дроби (x–1)4>0 всегда (кроме x=1), то знак второй производной зависит лишь от числителя. При x<0 y''<0, при x>0 y''>0.
, y''=0 при x=0. Так как знаменатель дроби (x–1)4>0 всегда (кроме x=1), то знак второй производной зависит лишь от числителя. При x<0 y''<0, при x>0 y''>0.
 и построить ее график.
и построить ее график. .
.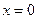 , тогда y=0.Пусть y=0, тогда
, тогда y=0.Пусть y=0, тогда  - решить уравнение точно не удается.
- решить уравнение точно не удается. пересечения графика с осями координат.
пересечения графика с осями координат.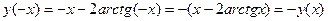 – функция нечетная.
– функция нечетная. .
. ,
, .
.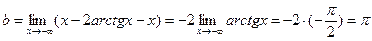 .
. - асимптота при
- асимптота при 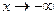 ,
,  - асимптота при
- асимптота при .
. ;
; 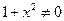 при
при  .
. , если
, если  , откуда
, откуда  и
и  - критические точки. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.
- критические точки. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.
 -1 1
-1 1 и
и  функция возрастает, а на интервале
функция возрастает, а на интервале  – убывает.
– убывает. ,
, 
 ;
;  , если
, если  , откуда
, откуда 
 - +
- + график выпуклый, а на интервале
график выпуклый, а на интервале  - выгнутый.
- выгнутый.  ,
,  .
.