 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Скалярное произведение, ортонормированный базис
Евклидовы пространства
Действительное линейное пространство E называется евклидовым, если каждой паре векторов I. II. III. IV. Число
Длина вектора Свойства: 1) 2) 3) 4)
Углом между векторами
Векторы Нормированные векторы
Вектор Если
Система векторов
называется ортонормированной. Во всяком пространстве
. . . . . . . . . . . . . . .
Пронормировав каждый вектор
Скалярное произведение, ортонормированный базис Будем говорить, что в n-мерном действительном линейном пространстве Vп определено скалярное умножение, если всякой паре векторов а, bпоставлено в соответствие действительное число, обозначаемое символом (а, b) и называемое скалярным произведением векторов аи b, причем выполняются следующие условия (здесь а, b, с - любые векторы пространства Vп , a- любое действительное число): I. (а, b) = (b, b). II. (а+b, с) = (а, с) + (b, с). III. (aа, b) = a(а, b). IV. Если а ¹ 0, то скалярный квадрат вектора а строго положителен, (а, а)>0. Отметим, что из III при а=0 следует равенство (0, b) = 0, (1) т. е. скалярное произведение нулевого вектора на любой вектор b равно нулю; равен нулю, в частности, скалярный квадрат нулевого вектора. Из II и III немедленно вытекает следующая формула для скалярного произведения линейных комбинаций двух систем векторов:
Если в n-мерном линейном пространстве определено скалярное умножение, то это пространство называется n-мернымевклидовым пространством. При любом п в п-мерном линейном пространстве Vп можно определить скалярное умножение, т. е. можно превратить это пространство в евклидово. В самом деле, возьмем в пространстве Vп любую базу е1, е2, .... еn. Если
то положим
Легко проверяется, что условия I - IV будут выполнены, т. е. равенство (1) определяет в пространстве Vп скалярное умножение. Как видно, что в n-мерном линейном пространстве скалярное умножение можно задать, вообще говоря, многими различными способами - определение (3) зависит, понятно, от выбора базы, а мы пока не знаем, кроме того, нельзя ли ввести скалярное умножение и каким-либо принципиально иным способом. Нашей ближайшей целью является обозрение всех возможных способов превращения n-мерного линейного пространства в евклидово пространство и установление того, что в некотором смысле для всякого п существует одно-единственное n-мерное евклидово пространство. Пусть дано произвольное n-мерное евклидово пространство Еп, т. е. в n-мерном линейном пространстве произвольным способом введено скалярное умножение. Векторы аи bназываются ортогональными, если их скалярное произведение равно нулю, (а,b) = 0. Из (1) следует, что нулевой вектор ортогонален к любому вектору; могут существовать, однако, и ненулевые ортогональные векторы. Система векторов называется ортогональной системой, если все векторы этой системы попарно ортогональны между собой. Всякая ортогональная система ненулевых векторов линейно независима. Пусть, в самом деле, в Еп дана система векторов b1, а2, ..., аk, причем, bi¹0, i=1, 2,…, k и (bi, bj) = 0 при i¹j. (4) Если a1а1+ a2а2+ …+akаk=0, то, скалярно умножая обе части этого равенства на вектор аi, 1£i£k, получаем ввиду (1), (2) и (4): 0=(0, аi)=(a1а1+ a2а2+ …+akаk, аi)= =a1(а1, аi)+ a2(а2, аi)+…+ ak(а k, аi)= ai(аi, аi) Отсюда, так как (аi, аi)>0 по IV, вытекает ai= 0, i=1, 2, . .., k, что и требовалось доказать. Сейчас будет описан процесс ортогонализации, т. е. некоторый способ перехода от любой линейно независимой системы из k векторов a1, а2, ..., аk, (5) евклидова пространства Еп к ортогональной системе, также состоящей из Н ненулевых векторов; эти векторы будут обозначены через b1, b2, ..., bk. Положим b1=а1, т. е. первый вектор системы (5) войдет и в строящуюся нами ортогональную систему. Положим, далее, b2 = a1b1 + а2. Так как b1 = а1, а векторы a1 и а2 линейно независимы, то векор b2отличен от нуля при любом числе a1. Подберем это число из условия, что вектор b2должен быть ортогонален к вектору b1; 0=(b1, b2)= (b1, a1b1 + а2)= a1(b1, b1) + (b1, a2) откуда, ввиду IV,
Пусть уже построена ортогональная система ненулевых векторов b1, b2, ..., bl.;дополнительно предположим, что для всякого i, 1£i£l, вектор bi является линейной комбинацией векторов а1 а2, ..., аi. Это предположение будет выполняться тогда и для вектора bi+1, если он будет выбран в виде bi+1=a1b1 +a2b2 + … +albl + al+1 Вектор bi+1 будет при этом отличен от нуля, так как система (5) линейно независимая, а вектор а1+1не входит в записи векторов b1, b2, ..., bl. Коэффициенты ai, i= 1, 2, . . ., l подберем из условия, что вектор bi+1 должен быть ортогонален ко всем векторам bi, i= 1, 2, . . ., l: 0=(bi, bl+1)= (bi, a1b1 +a2b2 + … +albl + al+1)= = a1(bi, b1) + a2(bi, b2) + …+al(bi, bl) + (bi, al+1); отсюда, так как векторы b1, b2, ..., bl ортогональны между собой, ai(bi, bi) + (bi, al+1)=0, т. е.
Продолжая этот процесс, мы построим искомую ортогональную систему b1, b2, ..., bk. Применяя процесс ортогонализации к произвольной базе пространства Еп, мы получим ортогональную систему из пненулевых векторов, т. е., так как эта система по доказанному линейно независима, ортогональную базу. При этом, используя замечание, сделанное в связи с первым шагом процесса ортогонализации, а также учитывая, что всякий ненулевой вектор можно включить в некоторую базу пространства, можно сформулировать даже следующее утверждение: Всякое евклидово пространство обладает ортогональными базами, причем любой ненулевой вектор этого пространства входит в состав некоторой ортогональной, базы. В дальнейшем важную роль будет играть один специальный вид ортогональных баз; базы этого вида соответствуют прямоугольным декартовым системам координат, используемым в аналитической геометрии. Назовем вектор b нормированным, если его скалярный квадрат равен единице, (b,b)=1 Если a¹0, откуда (а, а)>0, то нормированием вектора аназывается переход к вектору
Вектор bбудет нормированным, так как
База е1, е2, ..., еп евклидова пространства Еп называется орто-нормированной, если она ортогональна, а все ее векторы нормированы, т. е. (еi, еj) при i¹j, (еi, еj), i=1,2,…, n Всякое евклидово пространство обладает ортонормированными базами. Для доказательства достаточно взять любую ортогональную базу и нормировать все ее векторы. База останется при этом ортогональной, так как при любых a и b из (а, b) = 0 следует (aа, bb) = ab(а, b) = 0. База e1, e2,…, en евклидова пространства En тогда и только тогда будет ортонормированной, если скалярное произведение любых двух векторов пространства равно сумме произведений соответственных координат этих векторов в указанной базе, т. е. из следует Действительно, если для нашей базы выполняются равенства (6), то
Обратно, если выбранная база такова, что для любых векторов a и b, записанных в этой базе в виде (7), справедливо равенство (8), то, беря в качестве a и b любые два вектора этой базы ei и ej, различные или одинаковые, мы из (8) выведем равенство (6). Сопоставляя полученный сейчас результат с изложенным ранее доказательством существования n-мерных евклидовых пространств для любого n, можно сформулировать следующее утверждение: если в n-мерном линейном пространстве Vn выбрана произвольная база, то в Vп можно так задать скалярное умножение, что в полученном евклидовом пространстве выбранная база будет одной из ортонормированных баз.
ГРАМА МАТРИЦА - квадратная матрица
составленная из попарных скалярных произведений Если
то
где Аесть
Поиск по сайту: |
 сопоставляется число
сопоставляется число  так, что
так, что  и
и  выполняются аксиомы:
выполняются аксиомы:

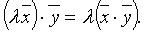

 называют скалярным произведением векторов
называют скалярным произведением векторов  и
и  ,
,  - скалярным квадратом вектора
- скалярным квадратом вектора  ). Введенная операция называется скалярным умножением векторов
). Введенная операция называется скалярным умножением векторов  - число
- число 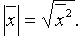


 (неравенство Коши-Буняковского);
(неравенство Коши-Буняковского); (неравенство треугольника).
(неравенство треугольника).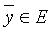 называют угол
называют угол  , для которого
, для которого


 то соответствующими этому вектору нормированными векторами будут
то соответствующими этому вектору нормированными векторами будут 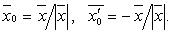
 для которой
для которой
 существует ортонормированный базис. Из произвольного базиса
существует ортонормированный базис. Из произвольного базиса  пространства
пространства  ортогональный базис может быть построен с помощью процесса ортогонализации:
ортогональный базис может быть построен с помощью процесса ортогонализации:
 где
где 
 где
где 
 где
где 
 получим ортонормированный базис. В ортонормированном базисе (
получим ортонормированный базис. В ортонормированном базисе (  ) для векторов
) для векторов 
 имеем:
имеем: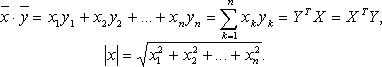
 (2)
(2)
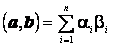 (3)
(3)
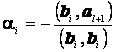


 (7)
(7)

 элементов (векторов) (пред)гильбертова пространства. Г. м. всегда неотрицательна. Она положительно определена, если а 1, а 2,..., а k линейно независимы. Справедливо обратное: любая неотрицательная (положительно определенная) (kx k)-матрица есть нек-рая Г. м. (с линейно независимыми определяющими векторами).
элементов (векторов) (пред)гильбертова пространства. Г. м. всегда неотрицательна. Она положительно определена, если а 1, а 2,..., а k линейно независимы. Справедливо обратное: любая неотрицательная (положительно определенная) (kx k)-матрица есть нек-рая Г. м. (с линейно независимыми определяющими векторами). суть га-мерные векторы (столбцы) n-мерного евклидова (эрмитова) пространства собычным скалярным произведением
суть га-мерные векторы (столбцы) n-мерного евклидова (эрмитова) пространства собычным скалярным произведением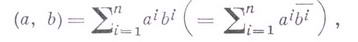

 -матрица, составленная из столбцов
-матрица, составленная из столбцов  ,
,  знак T означает операцию транспонирования матриц, а черта сверху - взятие комплексно сопряженной величины
знак T означает операцию транспонирования матриц, а черта сверху - взятие комплексно сопряженной величины