 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейная зависимость векторов
Векторы (элементы векторного, или, линейного, пространства) a1, a2, …, am являются линейно зависимыми, если равенство a1a1+a2a2+…+amam=0 возможно только при a1=a2=…=am=0. В противном случае, эти вектора называются линейно независимыми. Другими словами, вектора a1, a2, …, am являются линейно независимыми, если существуют не все равные нулю a1, a2, …, am такие, что имеет равенство a1a1+a2a2+…+amam=0. Если вектора a1, a2, …, am являются линейно независимыми, то некоторый из этих векторов является линейной комбинацией остальных. А именно, если для линейно зависимых векторов a1, a2, …, am имеем a1a1+a2a2+…+amam=0, a1≠0, то a1= Квадратичная форма Функция F(x1, x2, …, xn)= Квадратичная форма Аналогично, квадратичная форма называется положительно (отрицательно) полуопределённой, если для любого X выполняется неравенство Квадратичная форма называется знаконеопределённой, если существуют такие векторы X=(x1, x2, …, xn) и 1.6.1. Для того, чтобы матрица была положительно определённой, необходимо и достаточно, чтобы все угловые миноры матрицы были положительными: D1>0, D2>0, …, Dn>0. Для того, чтобы матрица была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с отрицательного: D1<0, D2>0, …, (-1)nDn>0. Для того, чтобы матрица была положительно полуопределённой, необходимо и достаточно, чтобы все главные миноры матрицы были ненулевыми. Для того, чтобы матрица была отрицательно полуопределённой, необходимо и достаточно, чтобы все главные миноры чётного порядка были неотрицательны, а все главные миноры нечётного порядка были неположительны. Таким образом, если для квадратичной формы не выполняется ни одно из вышеперечисленных условий 1.6, то она является знаконеопределённой. Ясно, что при достаточно больших п для проверки знакоопределённости квадратичной формы использование миноров (как угловых, так и главных) не очень удобно. Иногда удобно использование собственных векторов. 1.6.2. Для того, чтобы матрица была положительно определённой, необходимо и достаточно, чтобы все собственные значения были положительными: l1>0, l2>0, …, ln>0. Для того, чтобы матрица была отрицательно определённой, необходимо и достаточно, чтобы все собственные значения были отрицательными: l1<0, l2<0, …, ln<0. Для того, чтобы матрица была положительно полуопределённой, необходимо и достаточно, чтобы все собственные значения были неотрицательными: l1³0, l2³0, …, ln³0. Для того, чтобы матрица была отрицательно полуопределённой, необходимо и достаточно, чтобы все собственные значения были неположительными: l1£0, l2£0, …, ln£0. Наконец, квадратичная форма является знаконеопределённой тогда и только тогда, когда собственные значения матрицы квадратичной формы принимают различные знаки. Упражнения. 1.7.1.Решить системы методами Гаусса и Жордана-Гаусса: а) в) 1.7.2.Преобразовать систему методом Жордана-Гаусса с условием неотрицательности свободных членов: а) в) д) 1.7.3.Найти все угловые и главные миноры матриц: а) д) Решение. в) Имеем D1=a11=2, D2= D3= á(1) Разложили определитель по последнему столбцуñ Таким образом, D1=2, D2=3, D3=3 - значения угловых миноров. Найдём значения главных миноров. Обозначим через Далее, Ответ: D1=2, D2=3, D3=3 - угловые миноры;
1.7.4.Найти собственные векторы матриц: а) Решение. в) Для нахождения собственного вектора X матрицы A сначала ищем её собственные значения, решив характеристическое уравнение (1.3), и для каждого собственного значения l отдельно решаем систему (1.4) (ненулевые решения которой и образуют собственные векторы). Итак: 1) Решаем уравнение (1.3):
Û Таким образом, l1=1 и l2=3 - собственные значения матрицы. á(1) Разложили определитель по последнему столбцуñ 2) Отдельно для каждого собственного значения l решаем систему (1.4):
При l=1 имеем
Неизвестные x1 и x2 - свободные. Они принимают свободные значения: x2=a, x3=b. Тогда x1=x2=a. Таким образом, {(a, a, b)|a2+b2≠0} - множество всех собственных векторов матрицы, соответствующих собственному значению l=1. При l=3 имеем
Û В последней системе x3 - свободная переменная: x3=a. Тогда x2=-x3=-a, x1=-x2=-(-a)=a. Таким образом {(a, -a, a)|aÎR\{0}} - множество всех собственных векторов матрицы, соответствующих собственному значению l=3. Ответ: l1=1, X=(a, a, b), a2+b2≠0; l2=1, X=(a, -a, a), a≠0. 1.7.5. Проверить линейную зависимость векторов, и в случае линейной зависимости представить один из них в виде линейной комбинации остальных: а) a=(2, -1), b=(3, 2); б) a=(2, -1), b=(6, -3); в) a=(2, 1, -1), b=(3, 2, 1), c=(1, 2, 3); г) a=(1, 2, 3), b=(4, 5, 6), c=(7, 8, 9). Решение. а) Для выяснения линейной зависимости векторов a1, a2, …, am достаточно составить равенство a1a1+a2a2+…+amam=0 и выяснить, вытекает ли из него a1=a2=…=am=0, или существует ak≠0. В первом случае векторы линейно независимы, а во втором - линейно зависимы. В нашем случае aa+bb=0. Распишем это равенство и подвергнем его равносильным преобразованиям: aa+bb=0 Û a(2, -1)+b(3, 2)=(0, 0) Û (2a, -a)+(3b, 2b)=(0, 0) Û Û (2a+3b, -a+2b)=(0, 0) Û Полученная система имеет определитель D= д) Составим равенство aa+bb+gc=0 и подвергнем его преобразованиям: aa+bb+gc=0 Û a(1, 2, 3)+b(4, 5, 6)+g(7, 8, 9)=(0, 0, 0) Û Û (a+4b+7g, 2a+5b+8g, 3a+6b+9g)=(0, 0, 0) Û Полученную систему решим, например, методом Гаусса:
á(1) Первую строку, умноженную на 2 и 3, вычли из второй и третьей соответственно. (2) Вторую строку, умноженную на 2, вычли из третьей. Вторую разделили на -3ñ Таким образом, приходим к системе:
Нам достаточно найти какой-нибудь ненулевой набор a, b, g, задающий некоторое ненулевое решение системы. g - свободная неизвестная. Положим g=1. Тогда b=-2, a=-4b-7g=-4(-2)-7×1=1. Таким образом, a=1, b=-2, g=1, и a-2b+c=0. Коэффициент при a не равен 0 (a=1). Поэтому a можно выразить через остальные векторы (через b и c): a=2b-c. Вообще, так как b≠0 и g≠0, то b можно выразить через a и c, c - через a и b (выразите!) Ответ: а) Векторы линейно независимы. б) Векторы линейно зависимы; a=2b-c. 1.7.6.Исследовать на знакоопределённость квадратичную форму: а) -2 б) -2 в) -3 г) 5 Решение. а) Найдём матрицу этой формы: A= I способ. Найдём угловые миноры матрицы A: D1=-2<0, D2= Таким образом, угловые миноры квадратичной формы - знакочередующиеся, начиная с отрицательного. Следовательно, квадратичная форма является отрицательно определённой. II способ. Найдём собственные значения квадратичной формы:
= Поэтому l1=-2 - одно из собственных значений матрицы. Находим остальные собственные значения:
Ясно, что , и все собственные значения квадратичной формы являются отрицательными. Значит, квадратичная форма является отрицательно определённой. б) Матрица квадратичной формы: A= I способ. Угловые миноры матрицы A: D1=-2<0, D2= Так как D1<0 и D2<0, то необходимое и достаточное условие знакоопределённости уже не выполнено. Следовательно, квадратичная форма знакоопределённой не является. II способ. Найдём собственные значения квадратичной формы:
= = Поэтому l1=-2 - одно из собственных значений матрицы. Находим остальные собственные значения:
Так как собственные значения не имеют постоянного знака, то квадратичная форма не является знакоопределённой. á(1) Из первого столбца определителя вычли последний. (2) вынесли за определитель общий множитель первого столбца. (3) Первую строку определителя прибавили к третьей. (4) Разложили определитель по первому столбцуñ Ответ: а) Квадратичная форма является отрицательно определённой; б) квадратичная форма знакоопределённой не является.
§2. Евклидово пространство Rп. Множества в евклидовом пространстве. Последовательности в Rп. 2.1. Евклидово пространство Rп Множество Rп={(x1, x2, …, xn)| xiÎR} всевозможных упорядоченных наборов действительных чисел xi называется евклидовым пространством, если на этом множестве задана функция r: Rп´Rп®R по правилу: r(X, Y)= для любых точекX=(x1, x2, …, xn) и Y=(y1, y2, …, yn) из Rп. Число r(X, Y) называется расстоянием между точками X и Y. Например, если X=(3, -1, 2, 4) и Y=(2, 8, -4, 5), то r(X, Y)= 1.1.1. Расстояние между точками обладает следующими свойствами: 1о. r(X, Y)=r(Y, X) для любых точек X и Y. 2о. r(X, Y)³0, r(X, Y)=0 Û X=Y. 3о. r(X, Y)£r(X, Z)+r(Z, Y) для любых точек X, Y и Z. Таким образом, R1 - это числовая ось, R2 - плоскость с прямоугольной системой координат, R3 - обычное (геометрическое) пространство с прямоугольной системой координат.
Поиск по сайту: |
 a2+…+
a2+…+  am, и, вообще, если ak≠0, то ak=
am, и, вообще, если ak≠0, то ak=  a2+…+
a2+…+  ak-1+
ak-1+  ak+1+…+
ak+1+…+  am.
am. называется квадратичной формой от переменных x1, x2, …, xn, если aij=aji для всех i, jÎ{1, 2, …, n}. Матрицей квадратичной формы
называется квадратичной формой от переменных x1, x2, …, xn, если aij=aji для всех i, jÎ{1, 2, …, n}. Матрицей квадратичной формы  =(
=(  ,
,  , …,
, …,  ), что выполняются неравенства
), что выполняются неравенства  <0. Обозначение: А
<0. Обозначение: А  0.
0. б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 е)
е) 
 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  .
.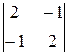 =2×2-(-1)×(-1)=4-1=3,
=2×2-(-1)×(-1)=4-1=3,
 1×(-1)3+3
1×(-1)3+3  ,
,  и т.д. - главные миноры первого порядка, через
и т.д. - главные миноры первого порядка, через  ,
,  , и т.д. - главные миноры второго порядка, и т.д. В нашем случае
, и т.д. - главные миноры второго порядка, и т.д. В нашем случае  =1 (получается вычёркиванием строк и столбцов под номерами 1 и 2).
=1 (получается вычёркиванием строк и столбцов под номерами 1 и 2). =2 (вычёркиваются вторые столбец и строка),
=2 (вычёркиваются вторые столбец и строка),  =
=  =2. Наконец,
=2. Наконец,  =D3=3 - единственный главный (он же и угловой) минор третьего порядка.
=D3=3 - единственный главный (он же и угловой) минор третьего порядка.
 ,
, Û
Û  =0 Û
=0 Û  Û
Û Û
Û 

 Û
Û  .
. Û
Û Û
Û  Û
Û 

 =7≠0, то есть является определённой однородной (имеет единственное, нулевое, решение). Значит, a=b=0.
=7≠0, то есть является определённой однородной (имеет единственное, нулевое, решение). Значит, a=b=0.




 -5
-5  -2
-2  +4х1х2+4х2х3;
+4х1х2+4х2х3; .
.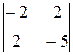 =10-4=6>0, D3=
=10-4=6>0, D3=  =-20+8+8=-4<0.
=-20+8+8=-4<0.







 D=49-8=41, l2, 3=
D=49-8=41, l2, 3=  .
. =-10-4=-14<0.
=-10-4=-14<0.







 l2=6, l3=-3.
l2=6, l3=-3. .
. =
= 