 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
РАЗДЕЛ III. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
§1. Произведение событий и условная вероятность. Определение 8. Произведением двух событий Если при нахождении вероятности не имеется никаких других ограничений, кроме необходимого комплекса условий, то такая вероятность называется безусловной. В противном случае она называется условной. Определение 9. Вероятность события Рассмотрим пример, поясняющий это определение. Пример 5. В ящике находится 11 деталей, из них 3 – нестандартные. Из ящика дважды безвозвратно берут по одной детали. Найти вероятность того, что во второй раз будет извлечена стандартная деталь( событие B), если в первый раз была извлечена нестандартная деталь( событие A) Решение. После первого извлечения в ящике из 10 деталей останется 8 стандартных, поэтому Пусть известны вероятность Теорема 3. Вероятность произведения двух событий определяется формулой
Пример 6. В условиях примера 1 найти вероятности того, что в первый раз извлечена нестандартная деталь, а второй раз стандартная, и наоборот. Решение. Пусть
2) Вероятность
Теорема 3 допускает обобщение на случай произведения любого числа событий
Т.е. вероятность совместного появления n событий равна произведению n вероятностей, где Пример 7. В урне находится 4 белых шара, 5 красных 3 синих. Наудачу извлекают по одному шару, не возвращая его обратно. Найти вероятность того, что в первый раз появится белый шар(событие A), во второй раз –красный(событие B), третий– синий(событие C) Решение. Вероятность появления белого шара в первый раз (событие A)
§2. Независимые события. Определение 10. Событие
Отсюда следует, что
Пример 8. Найти вероятность поражения цели при совместной стрельбе тремя орудиями, если вероятности поражения цели орудиями соответственно равны 0.9, 0.8 и 0.7. Решение. Введем события. Событие, состоящее в поражения цели первым орудием обозначим через
Иногда требуется найти вероятность проявления хотя бы одного события любого числа событий Теорема 4. Вероятность появления хотя бы одного события любого числа событий
Где Пример 9. В условиях примера 1 найти вероятность поражения( или хотя бы одного попадания) при залповой стрельбе.
§3. Обобщенные теоремы сложения и произведений вероятностей совместных событий: 3.1. Вероятность появления хотя бы одного из событий Рассмотрим примеры совместного использования теорем сложения и умножения. Пусть даны два независимых события
3.2. Теорема сложения вероятностей совместных событий. События Теорема 5. Вероятность суммы совместных событий определяется по формуле
1. для независимых событий
2. для зависимых:
3. независимых
3.3. Формула полной вероятности. Формула Байеса. Пусть события
Допустим, что события
Пример 10 . В двух урнах находятся белые и красные шары: в первой 4 белых и 5 красных, во второй 7 белых и 3 красных. Из второй урны наудачу взяли шар и переложили его в первую урну. Решение. Перекладывание из второй урны в первую белого шара( событие
Приведем теперь формулу Байеса. Пусть события
Допустим, что событие
Пример 11. Вероятность изготовления изделия с браком равна 0.08. После изготовления все изделия подвергаются проверке: изделия без брака признаются годными с вероятностью 0.95, а изделия с браком с вероятностью 0.06.Найти долю изделий, выпущенных после проверки, а также вероятность того, что выпущенное изделие окажется без брака. Решение. Введем гипотезы:
Для ответа на второй вопрос воспользуемся формулой
Поиск по сайту: |
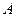 и
и 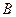 называется событие, означающее совместное появление этих событий.
называется событие, означающее совместное появление этих событий.
 .
.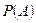 и условная вероятность
и условная вероятность  .
.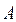 – событие, означающее, извлечение из ящика нестандартной детали, а событие
– событие, означающее, извлечение из ящика нестандартной детали, а событие 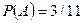 , а условная вероятность
, а условная вероятность 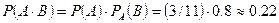 .
.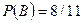 , а условная вероятность
, а условная вероятность  . Искомая вероятность
. Искомая вероятность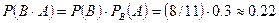 .
.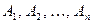 :
: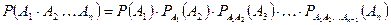 .,
., условные вероятности событий
условные вероятности событий  в предположении, что события
в предположении, что события  уже произошли.
уже произошли.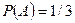 ; условная вероятность появления красного шара во втором извлечении при условии появления в первый раз белого шара
; условная вероятность появления красного шара во втором извлечении при условии появления в первый раз белого шара  . Условная вероятность появления синего шара в третьем извлечении при условии появления в предыдущих случаях белого и красного шаров
. Условная вероятность появления синего шара в третьем извлечении при условии появления в предыдущих случаях белого и красного шаров  Искомая вероятность определяется при
Искомая вероятность определяется при 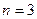 :
: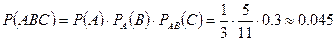 .
.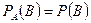 .
.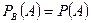 . Для независимых событий теорема умножения вероятностей принимает вид:
. Для независимых событий теорема умножения вероятностей принимает вид: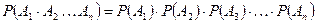 .
. – третьим. Поскольку эти события независимы, по теореме умножения при
– третьим. Поскольку эти события независимы, по теореме умножения при  .
.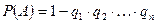 ,
, вероятности соответствующих противоположных событий.
вероятности соответствующих противоположных событий. и
и 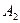 с вероятностями
с вероятностями и
и 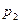 . Найдем вероятность появления только одного из них. Введем события
. Найдем вероятность появления только одного из них. Введем события 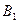 и
и 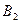 : событие
: событие 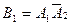 . Аналогично определим и событие
. Аналогично определим и событие  . Поскольку события
. Поскольку события  .
.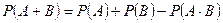 ;
;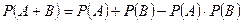 ;
;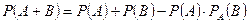 ;
;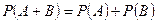 .
.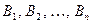 несовместны и образуют полную группу
несовместны и образуют полную группу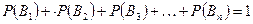 .
. при известных
при известных 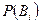 и
и  . Тогда вероятность события
. Тогда вероятность события 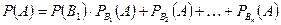
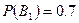 и
и 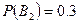 . Условные вероятности извлечения из первой урны белого шара(событие
. Условные вероятности извлечения из первой урны белого шара(событие 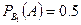 и
и 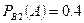 . Тогда по формуле полной вероятности получим:
. Тогда по формуле полной вероятности получим: .
.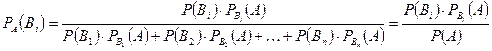
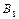 изделие без брака;
изделие без брака; 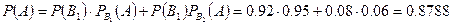 .
.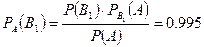 .
.