|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Закон розподілу Максвела⇐ ПредыдущаяСтр 17 из 17
Теплова або середня квадратична швидкість Максвел вирішив цю задачу про розподіл молекул ідеального газу за швидкостями постійного руху в стані теплової рівноваги. Він показав, що вірогідність того, що деяке число молекул dN із загального числа молекул N володіє швидкостями, що лежать у інтервалі від
f(v) - функція розподілу молекул за швидкостями dv - інтервал швидкостей, що розглядається Вигляд функції можна встановити на прикладі руху молекул ідеального газу в однорідному полі тяжіння. Спочатку розглянемо закон розподілу молекул по значенням вертикальної складової швидкості. Число молекул , що знаходяться в безкінечно тонкому шарі газу на висоті z, товщина dz:
n(z) – концентрація молекул газу на висоті z. Рухаючись як вільні, дані молекули через деякий інтервал часу перейдуть на висоту
При русі в полі тяжіння горизонтальні складові швидкості
Якщо продиференціювати це рівняння, при вибраних сталих значеннях
За час dt молекула на висоті z пройде шлях Якщо виключимо елементарний час dt, то:
Перемножимо почленно рівняння (6) і (7) і знайдемо:
Із урахуванням останнього виразу, рівняння (5) спрощується і приймає вигляд:
Використовуючи закон Больцмана у вигляді рівняння (2), отримаємо:
На основі закону збереження і перетворення енергії, знаходимо, що:
Тоді:
Звідси слідує, що:
В стані теплової рівноваги рух молекул газу буде рівновигідним по всіх напрямках. Так як вірогідність складної події, яка складається з незалежних подій, рівна добутку вірогідностей цих подій, то повні функція розподілу молекул за швидкостями буде мати вигляд:
Тоді:
З урахуванням рівняння (9), запишемо рівняння (5):
Така як тепловий рух молекул газу рівновірогідний у всіх напрямках, для визначення відношення Об’єм такого шару:
Ткаим чином, число молекул з швидкостями в інтервалі від v до v+dv буде чисельно дорівнювати:
Знайдемо вираз величини А. Так як інтервал швидкостей від нуля до нескінченності охоплює всі молекули, то очевидно, що інтеграл:
тоді:
Якщо зробити заміну змінних
З урахуванням цього, закон розподілу Максвела:
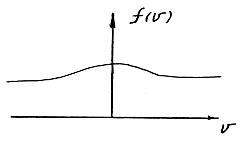
Графік функції рівняння (9) представляє собою Гаусову криву розподілу випадкової кривої:
Густина вірогідності розподілу молекул по швидкостям буде мати вигляд:
Як слідує з даного рівняння, при кожній температурі є деяка швидкість, яка має найбільше число молекул (цю швидкість називають найбільш вірогідною). Знайдемо вираз для цієї швидкості з урахуванням рівняння (12), дослідивши дане рівняння на екстремуми. Скоротивши в рівнянні (12) сталі величини і проінтегрувавши, отримаємо:
Звідси знаходимо вірогідну швидкість:
Середня арифметична швидкість молекул:
Стан газу можна характеризувати однією з трьох швидкостей: - вірогідною - середньою арифметичною - середньою квадратичною Наприклад:
p,V – тиск і об’єм. Співвідношення між цими швидкостями:
Поиск по сайту: |

 представляє собою середню характеристику теплового руху усієї сукупності мікрочастинок. В дійсності, всі мікрочастинки рухаються з різними швидкостями і можна поставити питання про розподіл мікрочастинок за швидкостями.
представляє собою середню характеристику теплового руху усієї сукупності мікрочастинок. В дійсності, всі мікрочастинки рухаються з різними швидкостями і можна поставити питання про розподіл мікрочастинок за швидкостями. до
до 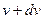 . Виражається дана вірогідність відношенням:
. Виражається дана вірогідність відношенням: (5)
(5)
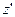 і займуть шар
і займуть шар 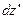 . При цьому, їх швидкості будуть лежати в інтегралі від
. При цьому, їх швидкості будуть лежати в інтегралі від 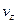 до
до  , але одне і те ж число молекул. Якщо прийняти, що
, але одне і те ж число молекул. Якщо прийняти, що 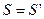 , то незмінність числа цих молекул виражається:
, то незмінність числа цих молекул виражається: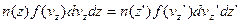 (6)
(6) - концентрація молекул газу на висоті
- концентрація молекул газу на висоті 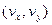 не будуть змінюватись, а зміна
не будуть змінюватись, а зміна 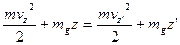
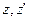 , отримаємо:
, отримаємо: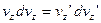
 , а на висоті
, а на висоті 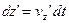
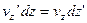 (7)
(7)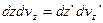
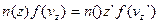
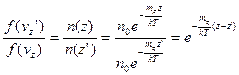
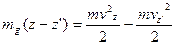
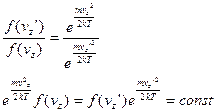
 (8)
(8)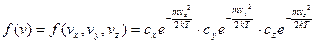


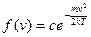 (9)
(9)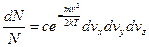 (10)
(10)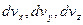 - об’єми нескінчено малого паралелепіпеда, що побудований в координатній системі простору швидкостей навколо точки з векторною координатою
- об’єми нескінчено малого паралелепіпеда, що побудований в координатній системі простору швидкостей навколо точки з векторною координатою 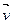 .
.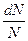 необхідно просумувати усі елементарні об’єми, що знаходяться на відстані
необхідно просумувати усі елементарні об’єми, що знаходяться на відстані 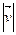 і ці об’єми заповнять шаровий прошарок між 2 нескінчено-близькими сферами з радіусами v i v+dv.
і ці об’єми заповнять шаровий прошарок між 2 нескінчено-близькими сферами з радіусами v i v+dv.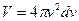
 (11)
(11)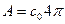 - деяка стала, що не залежить від швидкості молекул.
- деяка стала, що не залежить від швидкості молекул.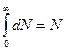
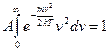
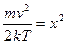 і скористатися значенням, що
і скористатися значенням, що 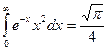 , то знайдемо:
, то знайдемо:
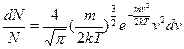 (12)
(12)

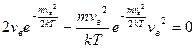
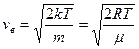 (13)
(13)