 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Правила дифференцирования ⇐ ПредыдущаяСтр 2 из 2
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C – постоянное число и f=f(x), g=g(x) – некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Если функция задана параметрически:
Дифференцирование сложной функции
Пример. Найти производную функции По правилу дифференцирования сложной функции:
В свою очередь производная
Производная вектор-функции Свойства производной вектор-функции:
Физический смысл производной Ключевые слова: физический смысл производной, среднее ускорение материальной точки, сила и импульс, количество заряда, напряженность и потенциал. Понятие производной широко используется в физике. Приведем несколько примеров. Средняя скорость точки выражается формулой Мгновенная скорость точки равна Среднее ускорение материальной точки выражается формулой Мгновенное ускорение точки равно Сила и импульс по второму закону Ньютона связаны соотношением Количество заряда, прошедшего через поперечное сечение проводника, определяет силу тока: В электростатическом поле, изменяющемся только по оси OX, проекция напряженности электрического поля и электрический потенциал связаны соотношением Мгновенная угловая скорость Мгновенное угловое ускорение Мощность Вторая производная Вторая производная – это производная от первой производной: Стандартные обозначения второй производной: Пример. Найдем вторую производную от функции Для того чтобы найти вторую производную, нужно сначала найти первую производную:
Теперь находим вторую производную:
Рассмотрим более содержательные примеры. Пример. Найти вторую производную функции Найдем первую производную:
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности, применив известную тригонометрическую формулу
Находим вторую производную:
Пример. Найти производную второго порядка от функции Находим первую производную как производную сложной функции:
Вторую производную находим как от произведения, предварительно вынеся по правилам дифференцирования коэффициент 3 за знак производной. Также будем учитывать, что первый множитель -
Пример. Найти производную функции Так как производная суммы равна сумме производных, то
Воспользуемся формулами для производных показательной и обратной тригонометрической функций:
Пример. Найти дифференциал третьего порядка функции По формуле
Найдем третью производную заданной функции:
Тогда
Пример. Найти производную неявно заданной функции
Продифференцируем обе части данного выражения по
Выразим из этого равенства
Пример. Найти производную
Решение. Найдем производные
Подставляя найденные значения
получим
Пример. Найти производную функции Применим логарифмическое дифференцирование:
Тогда, продифференцировав левую и правую часть, будем иметь:
Отсюда получаем, что
РЕШИТЬ СЛЕДУЮЩИЕ ЗАДАЧИ.
Задача 1.Тело массой 4 кг движется прямолинейно по закону х(t) = t2 + t + 1. Какова кинетическая энергия тела в конце третьей секунды движения после начала движения и сила, действующая на тело?
Задача 2.Материальная точка движется прямолинейно по закону x(t) = t2 – 4t + 3. Выведите формулу для вычисления скорости движения в любой момент времени t.
Задача 3.Точка движется по закону x(t) = t3 + 1. Найти ускорение в момент времени 1,0 c.
Задача 4.Заряд на пластинах конденсатора колебательного контура с течением времени изменяется по закону: q = 10-6sin104
Задача 5.Тело массой 4 кг движется прямолинейно по закону х(t) = t2 + t + 1. Какова кинетическая энергия тела в конце третьей секунды движения после начала движения и сила, действующая на тело?
Задача 6. Скорость школьного автобуса массой 5 т возрастает по закону υx = 0,1t3 + 0,2t. Определить равнодействующую всех сил, действующих на него в момент времени 2,0 с.
Поиск по сайту: |
 или
или 
 или
или 
 или
или 
 или
или 
 , то
, то  .
. .
.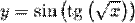 .
.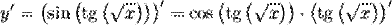 .
. также берется по правилу дифференцирования сложной функции:
также берется по правилу дифференцирования сложной функции: ,
, ,
, .
. – производная суммы есть сумма производных.
– производная суммы есть сумма производных. – здесь
– здесь 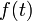 – дифференцируемая скалярная функция.
– дифференцируемая скалярная функция. – дифференцирование скалярного произведения.
– дифференцирование скалярного произведения. – дифференцирование векторного произведения.
– дифференцирование векторного произведения. – дифференцирование смешанного произведения.
– дифференцирование смешанного произведения. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. ,
,  или
или  (дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите
(дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите  .
. .
. .
. .
. .
. . Точнее говоря, использовать формулу будем в обратном направлении:
. Точнее говоря, использовать формулу будем в обратном направлении:  :
: .
. .
. .
.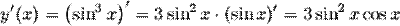 .
. - есть сложной функцией:
- есть сложной функцией:


 .
.
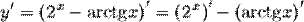 .
. .
. .
. .
.



 .
. .
.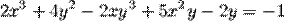
 , учитывая, что
, учитывая, что 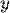 функция от
функция от 




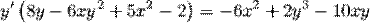

 от функции заданной параметрически
от функции заданной параметрически
 и
и 









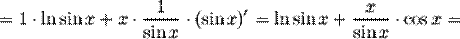

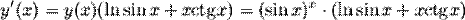
 t. Записать уравнение зависимости силы тока от времени.
t. Записать уравнение зависимости силы тока от времени.









