 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Скалярное произведение векторов. Угол между векторами
Скалярным произведением двух векторов Обозначение: Особые случаи:
Если векторы Угол между векторами выражается следующим образом:
В координатной форме: Пример 3.
Найти угол между векторами Решение: Обозначим: Ответ:
Векторное произведение векторов Определение: векторным произведением двух векторов
Направление Обозначение: Свойства: Допустим:
Тогда:
Доказательство:
Решаем систему по методу Крамера:
Таким образом:
Следствия: 1. 2.
4. 5. 6.
8.
Общее уравнение плоскости
Допустим:
Особые случаи:
Общее уравнение прямой в пространстве
Пример 1. Написать уравнение плоскости, проходящей через точки М1(–1;–2;0) и М2(1;1;2) и перпендикулярной к плоскости p: x + 2y + 2z – 4 = 0. Решение. Пусть M(x, y, z) – произвольная точка искомой плоскости.
Тогда векторы
Составим уравнение плоскости, содержащей векторы
Раскроем определитель третьего порядка:
Ответ: Пример 2. Написать уравнение прямой l, перпендикулярной плоскости p:
Решение. 1. 2. Тогда
Ответ:
III. Введение в теорию пределов функций
Определение: число А называется пределом функции y = f(x) при Обозначение: Основные свойства пределов:
Функция f(x) называется непрерывнойв данной точке a, если выполняется равенство: Замечательные пределы: 1. 2. Техника вычисления пределов
Пример 1. Найти Решение. Функция
Ответ: –8. Пример 2. Найти При непосредственном нахождении предела и числитель и знаменатель обращаются в нуль, таким образом, получается неопределенность вида Чтобы раскрыть неопределенность
и сократим дробь на выражение (х – 2), предел которого при
Тогда
Ответ: 7. Пример 3. Найти Решение: Непосредственно подстановкой убеждаемся, что выражение обращается в неопределенность вида Разложим числитель и знаменатель на множители:
и сократим дробь на выражение (х + 1). Таким образом
Ответ: ¥. Пример 4. Найти:
Решение: При Чтобы раскрыть неопределенность, разделим числитель и знаменатель дроби на наивысшую степень переменной –
Поскольку Ответ: 2. Пример 5. Найти: Решение. Непосредственно подстановкой имеем неопределенность
Ответ: 4. Пример 6. Найти: Решение: Найдем пределы, используя первый замечательный предел
Таким образом: Замечание:
Значит Ответ: Пример 7. Найти: Решение: Преобразуем выражение, стоящее под знаком предела, к виду
Если
Ответ: Рассмотрим теперь методику раскрытия неопределенностей вида 1¥ в точке, как всегда на конкретных примерах. ПРИМЕР 8. Вычислить предел: 9. Р = Аналогично, но без комментариев. ПРИМЕР 9
Теперь попроще и потому покороче ПРИМЕР 10.
ПРИМЕР 11
ПРИМЕР 12 а) б) в)
ПРИМЕР 13
ПРИМЕР 14
Поиск по сайту: |
 и
и  называется произведение модулей этих векторов на косинус угла между ними.
называется произведение модулей этих векторов на косинус угла между ними.
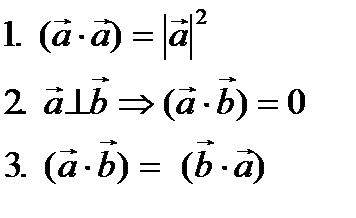
 и
и  то скалярное произведение вычисляется по формуле:
то скалярное произведение вычисляется по формуле: 


 и
и 
 .
.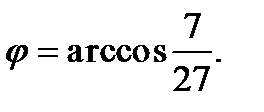

 , для которого выполняются следующие условия:
, для которого выполняются следующие условия:
 определяется правилом правого буравчика.
определяется правилом правого буравчика. .
. .
.
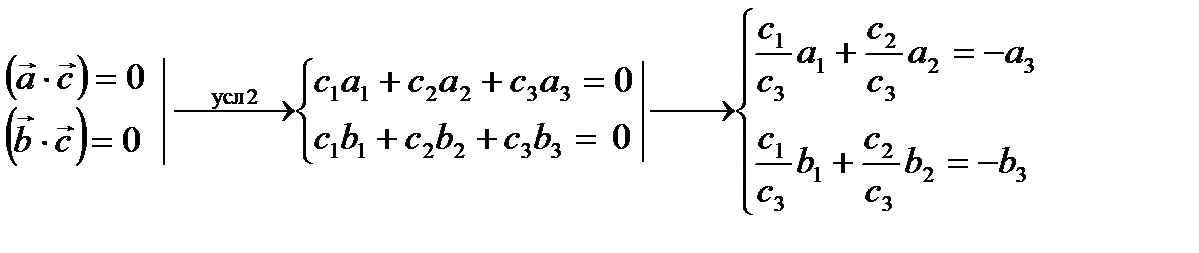


 ,
,  и
и  .
.
 .
. 3.
3.  (следствие 2).
(следствие 2). (следствие 2).
(следствие 2).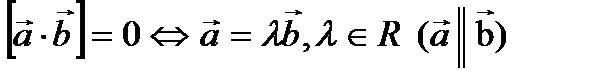 .
.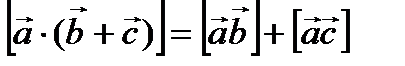 (следствие 2).
(следствие 2). 7.
7.  .
.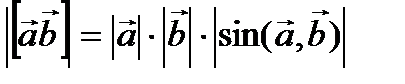 .
.
 нормальный вектор к плоскости;
нормальный вектор к плоскости; ;
;
 – уравнение плоскости общего вида.
– уравнение плоскости общего вида.

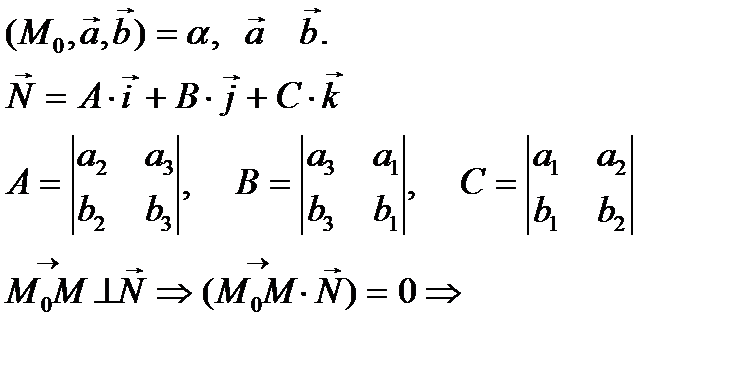


 – задание плоскости через определитель третьего порядка.
– задание плоскости через определитель третьего порядка.



 – уравнение прямой l, проходящей через данные точки М1(x1, y1, z1) и М2(x2, y2, z2).
– уравнение прямой l, проходящей через данные точки М1(x1, y1, z1) и М2(x2, y2, z2). 2.
2.  – уравнение прямой, заданной двумя пересекающимися плоскостями:
– уравнение прямой, заданной двумя пересекающимися плоскостями:

 лежат в одной плоскости, где
лежат в одной плоскости, где  – нормальный вектор к плоскости p.
– нормальный вектор к плоскости p.


 – уравнение плоскости.
– уравнение плоскости. , проходящей через точку
, проходящей через точку  .
.
 – нормальный вектор к плоскости p.
– нормальный вектор к плоскости p. , где точка М(x, y, z) лежит на искомой прямой l.
, где точка М(x, y, z) лежит на искомой прямой l.
 – уравнение прямой l.
– уравнение прямой l. .
. , если для любого числа
, если для любого числа  , существует
, существует  такое, что при
такое, что при  выполняется неравенство
выполняется неравенство  .
. .
.

 – первый замечательный предел.
– первый замечательный предел. – второй замечательный предел.
– второй замечательный предел. .
. – непрерывная, графиком ее является парабола. Следовательно, заменяя ее аргумент предельным значением, найдем значение предела:
– непрерывная, графиком ее является парабола. Следовательно, заменяя ее аргумент предельным значением, найдем значение предела: .
.
 .
. ,
, равен 0.
равен 0.
 .
.
 .
. .
. непосредственно подстановкой имеем неопределенность вида
непосредственно подстановкой имеем неопределенность вида  .
. . Тогда
. Тогда
 , то
, то  .
.
 . Раскроем неопределенность, умножив числитель и знаменатель на число, сопряженное к знаменателю дроби:
. Раскроем неопределенность, умножив числитель и знаменатель на число, сопряженное к знаменателю дроби: 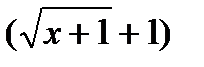
 . Тогда
. Тогда
 .
.


 .
. , так как если
, так как если  , то
, то  .
. .
.
 .
. ,
,  .
.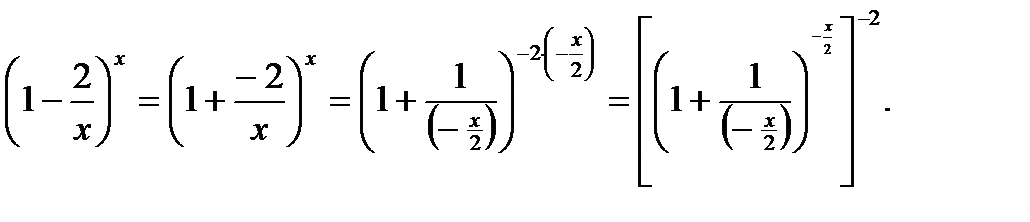
 . Значит:
. Значит:
 .
. = (выделим в скобках единицу) =
= (выделим в скобках единицу) =  = (в показателе выделим выражение обратное выражению 2(2 – х), получим)
= (в показателе выделим выражение обратное выражению 2(2 – х), получим)  .
.


 [неопределенность
[неопределенность 
 [неопределенность
[неопределенность 
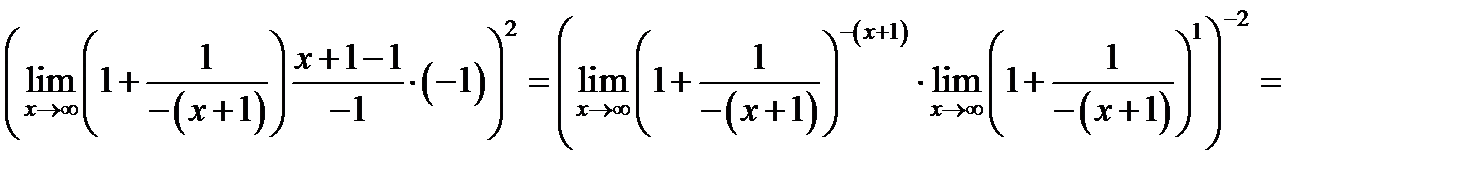
 [неопределенность
[неопределенность  а вот здесь получаем неопределенность
а вот здесь получаем неопределенность  ; перейдем к неопределенности
; перейдем к неопределенности  , для этого
, для этого
 имеем
имеем  , но вторая форма записи второго замечательного предела
, но вторая форма записи второго замечательного предела 
