 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ортогональные и ортонормированные базисы
Определение 3.5.Два вектора
Из определения скалярного произведения следует, что нулевой вектор Определение 3.6.Вектор Если Определение 3.7.Система векторов
Теорема 3.5. Любая ортогональная система □ Составим равенство
где
откуда
Так как
Умножив равенство (3.10) скалярно на вектор Теорема 3.6. Если
□ Вычислим скалярный квадрат вектора
откуда и следует равенство (3.11). ■ Пусть далее Определение 3.8.Если базис
то он называется ортогональным базисом евклидова пространства Определение 3.9.Вектор
Очевидно, что любой ненулевой вектор
При этом говорят, что вектор Определение 3.10.Ортогональный базис
Использование ортонормированного базиса облегчает вычисление скалярного произведения в координатной форме. Пусть
где Матрица Грама для системы векторов
Тогда скалярное произведение (3.5) в ортонормированном базисе
В ортонормированном базисе также упрощается вычисление координат вектора – они вычисляются через скалярные произведения. Если разложение вектора
то умножив обе части последнего равенства скалярно на
Тогда разложение вектора
Поиск по сайту: |
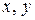 евклидового пространства
евклидового пространства 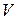 называются ортогональными, если их скалярное произведение равно нулю:
называются ортогональными, если их скалярное произведение равно нулю: .
. ортогонален любому вектору
ортогонален любому вектору 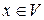 .
. , если он ортогонален каждому вектору этого подпространства.
, если он ортогонален каждому вектору этого подпространства. , то вектор
, то вектор  тогда и только тогда, когда
тогда и только тогда, когда  .
. евклидова пространства
евклидова пространства  ,
,  ,
,  .
. , (3.9)
, (3.9) некоторые действительные числа. Умножив равенство (3.9) скалярно на вектор
некоторые действительные числа. Умножив равенство (3.9) скалярно на вектор  , на основании свойств скалярного произведения получим:
, на основании свойств скалярного произведения получим: ,
, .
. , то равенство (3.9) примет вид
, то равенство (3.9) примет вид , (3.10)
, (3.10) , получим
, получим  . И так далее. Окончательно получаем, что все коэффициенты
. И так далее. Окончательно получаем, что все коэффициенты  равны нулю. Тогда по определению система ненулевых векторов
равны нулю. Тогда по определению система ненулевых векторов 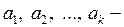 ортогональная система векторов, то выполняется равенство
ортогональная система векторов, то выполняется равенство (3.11)
(3.11) :
: ,
, ) евклидово пространство.
) евклидово пространство. евклидова пространства
евклидова пространства  ,
,  ,
, называется единичным, если его евклидова норма равна единице:
называется единичным, если его евклидова норма равна единице: .
. можно преобразовать в единичный вектор
можно преобразовать в единичный вектор  следующим образом:
следующим образом: .
. называют нормирующим множителем.
называют нормирующим множителем. евклидова пространства
евклидова пространства  (
(  ) этого базиса – единичный, то есть
) этого базиса – единичный, то есть

 координатные вектор-столбцы.
координатные вектор-столбцы. в этом случае имеет вид
в этом случае имеет вид .
. примет наиболее простой вид
примет наиболее простой вид . (3.12)
. (3.12) по ортонормированному базису
по ортонормированному базису  ,
, (
(  ), получим
), получим .
. .
.