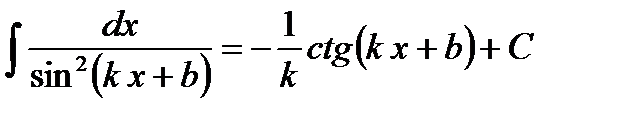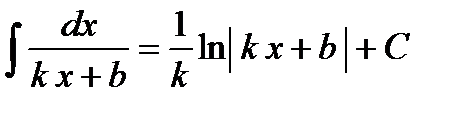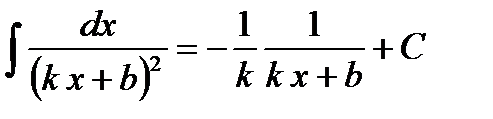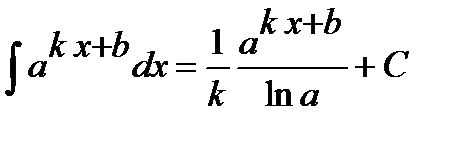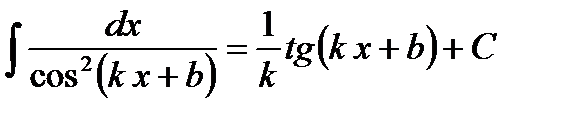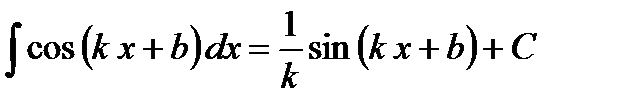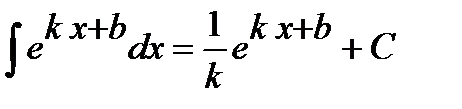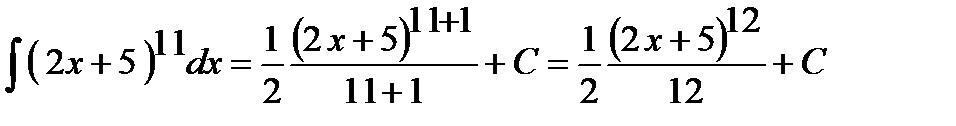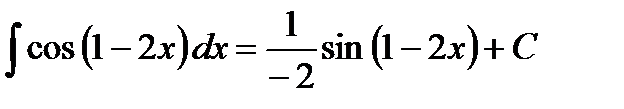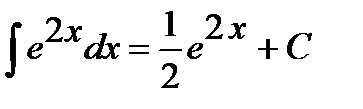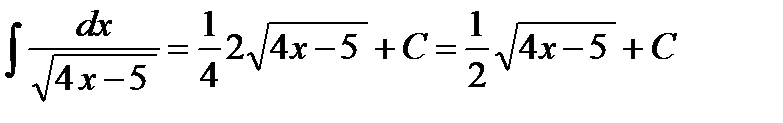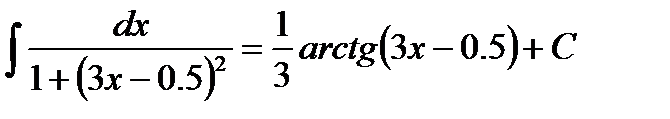|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Замена переменной (или подведение под знак дифференциала)
Сведения из теории Вспомним правило дифференцирования сложной функции. Пусть дана сложная функция Вернемся к задаче интегрирования. Как правило, искомый интеграл всегда дается в виде
Замечание В учебной литературе этот процесс замены переменной часто называется подведением под знак дифференциала. Поясним смысл этого названия. Пусть увидели в интеграле нужную структуру, т.е.
По определению произведение вида
Образно говоря, производная Пример 5.Найти интеграл Решение. Выделим нужную структуру
Ответ. Пример 6. Найти интеграл Решение. Единственный табличный интеграл, содержащий показательную функцию, это интеграл
Ответ.
Пример 7. Найти интеграл Решение. Имеем табличный интеграл
Ответ. Пример 8. Найти интеграл Решение. Будем ориентироваться на табличный интеграл
В нем аргумент синуса и переменная интегрирования должны быть абсолютно одинаковыми. В искомом интеграле изменить аргумент синуса
Ответ. Пример 9. Найти интеграл Решение. В таблице имеем интеграл
Ответ. Проанализируем полученный результат. Первообразная осталась та же, что и в табличном интеграле – натуральный логарифм модуля. Логарифмируемое выражение совпало со знаменателем в искомом интеграле. Перед первообразной функцией добавился сомножитель обратный коэффициенту при х. Все это является проявлением общего правила, полученного на основе замены переменной. Пусть известно, что Из него, в частности, следует расширение таблицы интегралов:
Применение этого правила можно видеть на следующих примерах: 1. 2. 3. 4. 5. 6. 7.
Поиск по сайту: |
 . Ее производная функция вычисляется по формуле
. Ее производная функция вычисляется по формуле 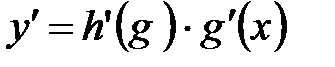 . Из формулы видно, что сначала вычисляется производная внешней функции
. Из формулы видно, что сначала вычисляется производная внешней функции 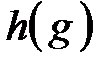 , а потом эта производная умножается на производную внутренней функции
, а потом эта производная умножается на производную внутренней функции  .
.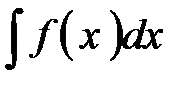 . Вы сами должны увидеть, имеет ли подынтегральная функция структуру
. Вы сами должны увидеть, имеет ли подынтегральная функция структуру  или, хотя бы, близкую к ней. Если Вы эту структуру увидели, то Вы поняли, какую формулу имеет внутренняя функция
или, хотя бы, близкую к ней. Если Вы эту структуру увидели, то Вы поняли, какую формулу имеет внутренняя функция 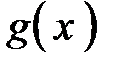 . После этого Вы обозначаете внутреннюю функцию как новую переменную
. После этого Вы обозначаете внутреннюю функцию как новую переменную 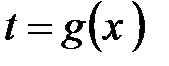 . Тогда
. Тогда 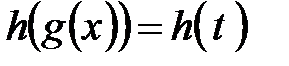 . Нельзяпросто механически заменить символ
. Нельзяпросто механически заменить символ 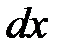 на символ
на символ 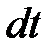 . Предварительно найдем дифференциал новой переменной
. Предварительно найдем дифференциал новой переменной 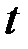 :
: 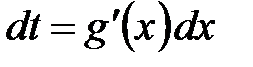 . Теперь в исходном интеграле можно перейти к новой переменной интегрирования.
. Теперь в исходном интеграле можно перейти к новой переменной интегрирования.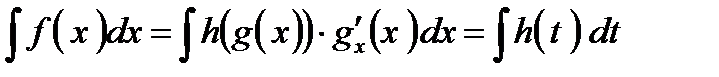 .
.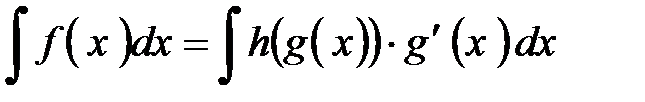 .
. равно дифференциалу функции
равно дифференциалу функции  , т.е.
, т.е. 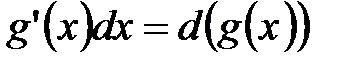 . Тогда процесс замены переменной интегрирования будет выглядеть так:
. Тогда процесс замены переменной интегрирования будет выглядеть так:
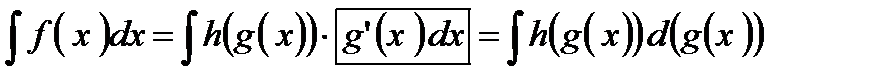
 перемещается вправо за символ
перемещается вправо за символ  , превращаясь при этом в свою первообразную
, превращаясь при этом в свою первообразную  . В этом и заключается подведение под знак дифференциала.
. В этом и заключается подведение под знак дифференциала.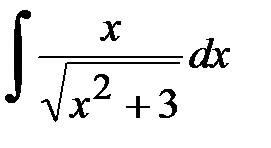 .
.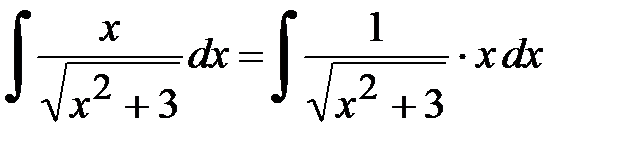 . Замена
. Замена 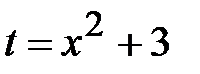 . Заготовка
. Заготовка  . После подстановки в искомый интеграл получаем
. После подстановки в искомый интеграл получаем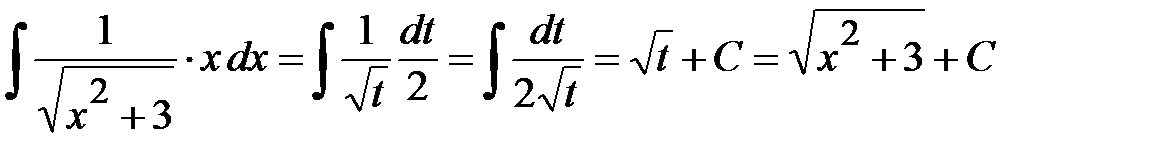 .
.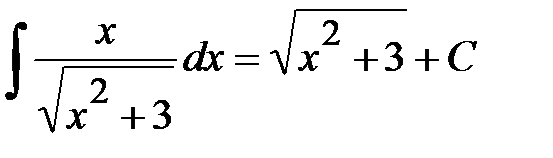 .
.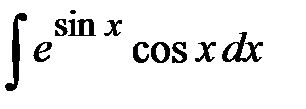 .
.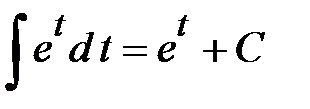 . Чтобы прийти к нему, сделаем замену
. Чтобы прийти к нему, сделаем замену 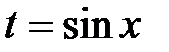 . Вычислим
. Вычислим 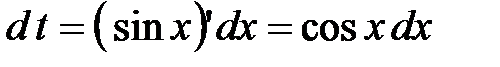 . Подставим в искомый интеграл:
. Подставим в искомый интеграл: .
.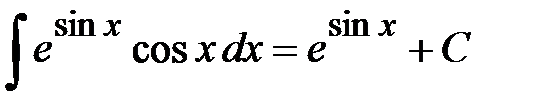
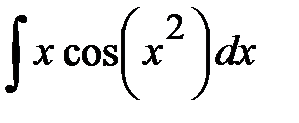 .
.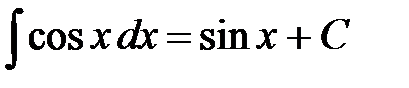 . В искомом интеграле обозначим
. В искомом интеграле обозначим 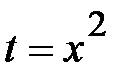 . Подготовим
. Подготовим  . После подстановки в искомый интеграл получим
. После подстановки в искомый интеграл получим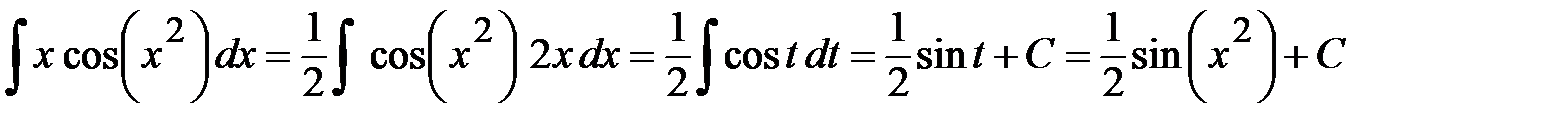 .
.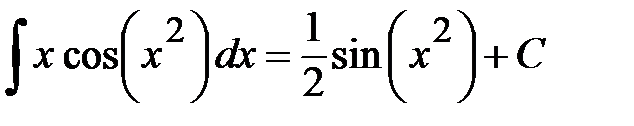 .
.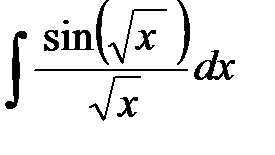 .
.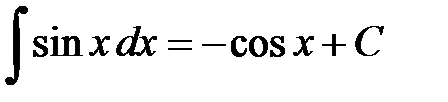 .
.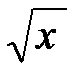 мы не можем. Значит надо сделать так, чтобы переменной интегрирования стал
мы не можем. Значит надо сделать так, чтобы переменной интегрирования стал 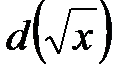 :
:  . В искомом интеграле умножим числитель и знаменатель на 2 и выполним цепочку преобразований:
. В искомом интеграле умножим числитель и знаменатель на 2 и выполним цепочку преобразований: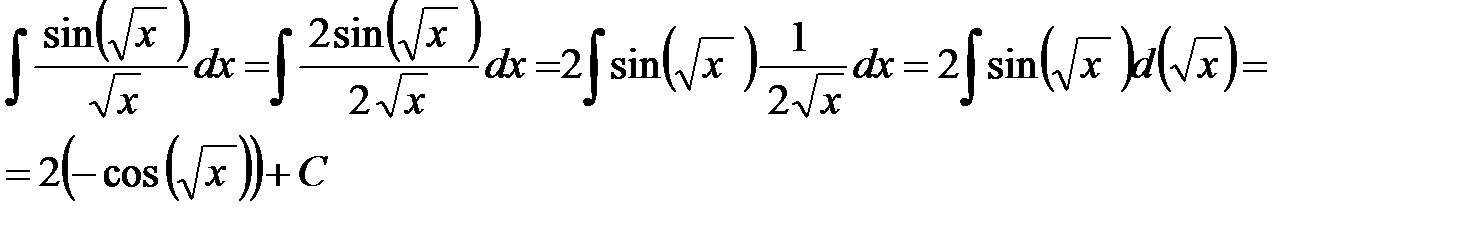
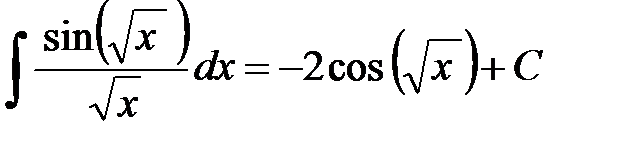 .
. .
.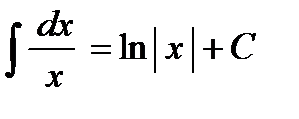 . Попытаемся искомый интеграл свести к данному табличному. Не будем изменять знаменатель. Сделаем замену переменной, обозначив
. Попытаемся искомый интеграл свести к данному табличному. Не будем изменять знаменатель. Сделаем замену переменной, обозначив  . Вычислим формулу, выражающую дифференциал новой переменной t через дифференциал старой переменной х:
. Вычислим формулу, выражающую дифференциал новой переменной t через дифференциал старой переменной х: 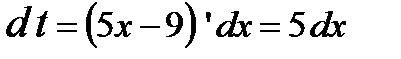 . Тогда
. Тогда  . Подставим все заготовки в искомый интеграл.
. Подставим все заготовки в искомый интеграл.
 .
.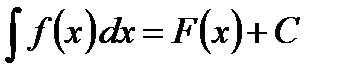 (как правило, из таблицы интегралов). Тогда
(как правило, из таблицы интегралов). Тогда 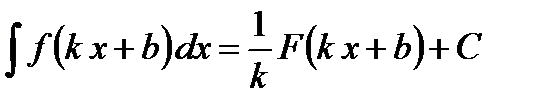 .
.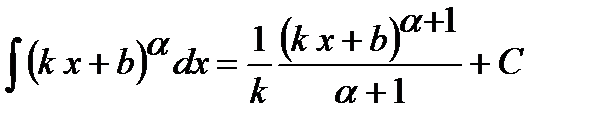 ,
если
,
если  .
.