 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Числовые характеристики статистических рядов⇐ ПредыдущаяСтр 20 из 20
Наиболее распространенными характеристиками совокупности являются: 1) среднее арифметическое 2) среднее квадратическое (или стандартное) отклонение 3) стандартная ошибка среднего арифметического 4) коэффициент вариации (V). 1. Средним арифметическим называетсячастное от деления суммы всех значений вариант рассматриваемой совокупности на их число (n):
Среднее арифметическое обладает следующими свойствами: а) измеряется в тех же единицах, что и основные варианты; б) если каждое число совокупности уменьшить (увеличить) на одно и то же число, то ее среднее уменьшится (увеличится) на это же число; в) если каждое число совокупности увеличить (уменьшить) в несколько раз, то ее среднее увеличится (уменьшится) в такое же число раз; г) сумма отклонений статистических данных совокупности от их точного среднего всегда равна нулю: 2. Среднее квадратическое (или стандартное) отклонение Основной мерой статистического измерения изменчивости признака у членов совокупности служит среднее квадратическое отклонение В основе среднего квадратического отклонения лежит сопоставление каждой варианты Величина Свойства стандартного отклонения: 1. Стандартное отклонение всегда измеряется в тех же единицах измерения, что и основные варианты. 2. Чем больше 3. В вариационных рядах с нормальным распределением частот 99,7% всех членов совокупности находящихся в границах от 4. При вычислении стандартное отклонение определяют с точностью на один десятичный знак больше, чем точность, которую применяют для вычисления средней арифметической для того же ряда. 3. Стандартная ошибка средней арифметической или ошибка репрезентативности Стандартная ошибка средней вычисляется по формуле: В современной научной литературе средняя арифметическая представляется вместе с ошибкой репрезентативности:
4. Коэффициент вариации (V).Изложенные выше характеристики совокупности (средняя арифметическая и стандартное отклонение) имеют один недостаток: они дают показатель изменчивости признака в именованных величинах, а не в относительных. Поэтому сопоставление (или сравнение) разноименных признаков по этим параметрам невозможно. В этом случае удобно пользоваться коэффициентом изменчивости признака, который выражается в относительных величинах, а именно в процентах, и вычисляется по формуле:
Считается, что если V<=10% то выборку можно считать однородной, т.е. полученной из одной генеральной совокупности. Колеблемость (изменчивость) результатов измерений в зависимости от величины коэффициента вариации считают небольшой (до 10%), средней (11-20%) и большой (более 20%). Если V>20%, то выборка некомпактна по заданному признаку.
Пример. Определить основные статистические показатели результатов прыжка в длину группы спортсменов, если данные выборки таковы: xi,см~185,171,190,170,190,178,188,174,193,178,176,180,175,176,180,192 (n=16). Решение: 1. Для определения среднего арифметического используем формулу:
3. Стандартное отклонение вычислим по формуле: 4. Определим стандартную ошибку среднего арифметического, используя формулу:
5. Определим коэффициент вариации по формуле:
Выводы: 1) среднее значение высоты прыжка составляет181 см; 2) по показателю высоты прыжка группа компактна, т.к. стандартное отклонение составляет ± 7,6 см, а коэффициент вариации —4, 2 % (менее 10%). Вопросы для самопроверки: 1) Приведите примеры механической, серийной, типической и комбинированной выборок. 2) Какие существуют формы представления статистических данных? 3) В каком случае для изображения вариационного ряда используется полигон распределения, а в каком гистограмма? 4) Перечислите основные свойства, которыми обладает среднее арифметическое. 5) Что называется средним квадратическим отклонением?
Упражнения для самостоятельного выполнения: 1.Выборка состоит из всех букв, входящих в двустишие «...Это дерево - сосна, И судьба сосны ясна...». а) Выпишите ряд данных выборки. б) Найдите объем выборки. в) Определите кратность и частоту варианты «о». г) Какова наибольшая процентная частота вариант выборки? 2.При выборочной переписи населения в 20 квартирах были получены следующие сведения о годах рождения их жильцов (первые две цифры 1 и 9 не пишем): 30, 56, 98, 77, 93, 31, 61, 80, 87, 52, 56, 32, 87, 73, 93, 81, 57, 52, 61, 87, 90, 92, 85, 87, 70, 61, 93, 87, 52, 53, 40, 56, 48, 51, 61, 87, 88, 90, 52, 60, 22, 34, 48, 52, 88, 87, 91, 62, 63, 87, 39, 40, 52, 87, 99, 91, 87, 65, 61, 55. а) Каков общий ряд данных этого измерения? б) Составьте ряд данных. в) Найдите кратность и частоту вариант 61 и 87. г) Составьте таблицу кратностей, разбив данные на интервалы 3. В фермерском хозяйстве площади, отведенные под посевы зерновых, распределены следующим образом: пшеница – 63%, овес – 16%, просо – 12 %, гречиха – 9%. Постройте круговую диаграмму, иллюстрирующую распределение площадей, отведенных под зерновые. 4. Наблюдая за работой бригады токарей, установили, сколько времени тратили они на обработку одной детали. Обобщая полученные данные, составили таблицу:
Пользуясь таблицей, постройте гистограмму, характеризующую распределение токарей по времени, затрачиваемому на обработку одной детали. Преобразуйте гистограмму в полигон, заменяя каждый интервал его серединой.
Пользуясь гистограммой, найдите: а) число рабочих цеха в возрасте от 18 до 23 лет; б) возрастную группу, к которой относится наибольшее число в) общее число рабочих цеха. 6.Найдите среднее арифметическое, размах и моду ряда чисел: а) 16, 22, 16, 13,20, 17; б)-21,-33,-35,-19,-20,-22. 7. Найти выборочную среднюю и выборочную дисперсию по данному распределению выборки объема 10. хi 3 5 6 7 ni 4 2 1 3 Список литературы
Ресурсы Интернета http://www.en.edu.ru/ Естественно-научный образовательный портал. Портал является составной частью федерального портала "Российское образование". Содержит ресурсы и ссылки на ресурсы по естественно-научным дисциплинам (математика, физика, химия и биология). Ссылки на образовательные ресурсы систематизированы по разделам науки.
http://ilib.mccme.ru/ Интернет библиотека Московского Центра непрерывного математического образования. Золотой фонд популярной физико-математической литературы. Замечательные книги, бывшие в течение десятков лет настольными для многих школьных учителей математики, руководителей кружков, школьников, интересующихся точными науками. Одним из основных форматов представления графических файлов служит формат DjVu, сочетающий сравнительно небольшой объем с достаточной читаемостью. http://ilib.mccme.ru/plm/ Серия "Популярные лекции по математике" Московского Центра непрерывного математического образования. Для каждого издания приведены аннотация и содержание.
http://www.sci-lib.com/ Большая Научная Библиотека. 1824 электронных книг и учебников общим объемом более 12.2 GB в формате DJVU или PDF. БНБ является полностью бесплатной библиотекой. Также на страницах Большой Научной Библиотеки (БНБ) DJVU книг можно будет заказать и свободно скачать практически любую научную статью из более чем 6000 электронных журналов крупнейших академических издательств таких как Elsevier, Kluwer, Oxford University Press, Cambridge University Press, Blackwell Publishers и многих других. Раздел математики в виртуальной библиотеке БНБ – http://sci-lib.com/subject.php?subject=1&pp=1. Издания располагаются по разделам математики в алфавитном порядке.
СОДЕРЖАНИЕ
Поиск по сайту: |

 ;
; ;
; .
.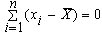 .
. .
. со средней арифметической данной совокупности. Так как .
со средней арифметической данной совокупности. Так как . 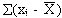 всегда равна нулю, то для измерения изменчивости берут отклонение в квадрате, т.е.
всегда равна нулю, то для измерения изменчивости берут отклонение в квадрате, т.е.  Если просуммировать квадраты отклонений, то эта сумма не будет равна нулю. А чтобы получить коэффициент, способный измерить изменчивость, берут среднее отклонение из выражения:
Если просуммировать квадраты отклонений, то эта сумма не будет равна нулю. А чтобы получить коэффициент, способный измерить изменчивость, берут среднее отклонение из выражения: 
 называется взвешенной дисперсией. Тогда стандартное отклонение
называется взвешенной дисперсией. Тогда стандартное отклонение 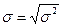
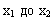 , которые отстоят от средней арифметической на величину от
, которые отстоят от средней арифметической на величину от  . За пределами
. За пределами  находятся только 0,3% всех членов совокупности.
находятся только 0,3% всех членов совокупности.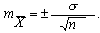
 .
.

 , σ=
, σ= 



